
сборник задач для картфака
.docНомер варианта соответствует порядковому номеру фамилии студента в журнале группы. Решение задачи должно включать ее условие, последовательное изложение процесса решения с комментариями и рисунком, ответ в общем виде и численные расчеты в системе единиц СИ.
|
№ вар. |
НОМЕРА ЗАДАЧ |
|||||||
|
1 |
1 |
16 |
41 |
54 |
75 |
76 |
|
|
|
2 |
2 |
17 |
42 |
55 |
74 |
77 |
|
|
|
3 |
3 |
18 |
43 |
56 |
73 |
78 |
|
|
|
4 |
4 |
19 |
44 |
57 |
72 |
79 |
|
|
|
5 |
5 |
20 |
45 |
58 |
71 |
80 |
|
|
|
6 |
6 |
21 |
32 |
59 |
70 |
81 |
|
|
|
7 |
7 |
22 |
33 |
60 |
69 |
82 |
|
|
|
8 |
8 |
23 |
34 |
57 |
68 |
83 |
|
|
|
9 |
9 |
24 |
35 |
58 |
67 |
84 |
|
|
|
10 |
10 |
25 |
36 |
59 |
66 |
85 |
|
|
|
11 |
11 |
26 |
37 |
46 |
64 |
86 |
|
|
|
12 |
12 |
27 |
38 |
47 |
63 |
87 |
|
|
|
13 |
13 |
28 |
39 |
48 |
62 |
88 |
|
|
|
14 |
14 |
29 |
40 |
49 |
61 |
89 |
|
|
|
15 |
15 |
30 |
31 |
50 |
65 |
90 |
|
|
|
16 |
5 |
29 |
32 |
51 |
70 |
76 |
|
|
|
17 |
8 |
28 |
33 |
52 |
71 |
77 |
|
|
|
18 |
7 |
27 |
34 |
53 |
72 |
78 |
|
|
|
19 |
6 |
26 |
35 |
46 |
73 |
79 |
|
|
|
20 |
9 |
25 |
41 |
54 |
74 |
80 |
|
|
|
21 |
10 |
24 |
42 |
55 |
75 |
81 |
|
|
|
22 |
11 |
23 |
43 |
56 |
61 |
82 |
|
|
|
23 |
12 |
22 |
44 |
60 |
62 |
83 |
|
|
|
24 |
1 |
21 |
45 |
59 |
63 |
84 |
|
|
|
25 |
2 |
20 |
36 |
58 |
64 |
85 |
|
|
|
26 |
3 |
19 |
37 |
57 |
65 |
86 |
|
|
|
27 |
13 |
18 |
38 |
56 |
66 |
87 |
|
|
|
28 |
4 |
17 |
39 |
55 |
67 |
88 |
|
|
|
29 |
14 |
16 |
40 |
54 |
68 |
89 |
|
|
|
30 |
15 |
30 |
31 |
53 |
69 |
90 |
|
|
-
Материальная точка вращается вокруг неподвижной оси по закону
 ,
где
,
где
 = 10 рад,
= 10 рад,
 = 20 рад/с,
= 20 рад/с,
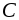 = 2
рад/с2 . Найти полное ускорение
точки, находящейся на расстоянии R
= 0,1 м от оси вращения, для момента времени
t = 4 с.
= 2
рад/с2 . Найти полное ускорение
точки, находящейся на расстоянии R
= 0,1 м от оси вращения, для момента времени
t = 4 с. -
Закон движения материальной точки имеет вид:
 . Найти перемещение и пройденный путь
за промежуток времени от t1
= 2 c до t2
= 4 c, а также среднюю
путевую скорость и среднюю скорость
перемещения.
. Найти перемещение и пройденный путь
за промежуток времени от t1
= 2 c до t2
= 4 c, а также среднюю
путевую скорость и среднюю скорость
перемещения. -
Материальная точка движется по закону:
 , где
, где
 = 6 м/с,
= 6 м/с,
 = 0,2 м/с2,
= 0,2 м/с2,
 = 0,125 м/с4 .
Найти скорость и ускорение точки в
моменты времени t1
= 0 c и t2
= 2 с, а также среднюю скорость перемещения
и среднее ускорение за первые 2 с
движения.
= 0,125 м/с4 .
Найти скорость и ускорение точки в
моменты времени t1
= 0 c и t2
= 2 с, а также среднюю скорость перемещения
и среднее ускорение за первые 2 с
движения. -
Определить полное ускорение в момент t = 3 с материальной точки, находящейся на ободе колеса радиусом R = 0,5 м, вращающегося согласно уравнению
 ,
где
,
где
 = 2 рад/с и
= 2 рад/с и
 = 0,2 рад/с3.
= 0,2 рад/с3. -
Материальная точка вращается вокруг неподвижной оси по закону
 , где
, где
 = 10 рад,
= 10 рад,
 = 0,5 рад/с3,
= 0,5 рад/с3,
 = 2
рад/с2 . Найти полное ускорение
точки, находящейся на расстоянии R
= 0,1 м от оси вращения, для момента времени
t = 3 с.
= 2
рад/с2 . Найти полное ускорение
точки, находящейся на расстоянии R
= 0,1 м от оси вращения, для момента времени
t = 3 с. -
Закон движения материальной точки имеет вид:
 .,
где
.,
где
 ,
,
 .
Найти перемещение, пройденный путь,
среднюю путевую скорость и среднюю
скорость перемещения для промежутка
времени от t1 = 2 с
до t2 = 6 c.
.
Найти перемещение, пройденный путь,
среднюю путевую скорость и среднюю
скорость перемещения для промежутка
времени от t1 = 2 с
до t2 = 6 c. -
Материальная точка движется по закону:
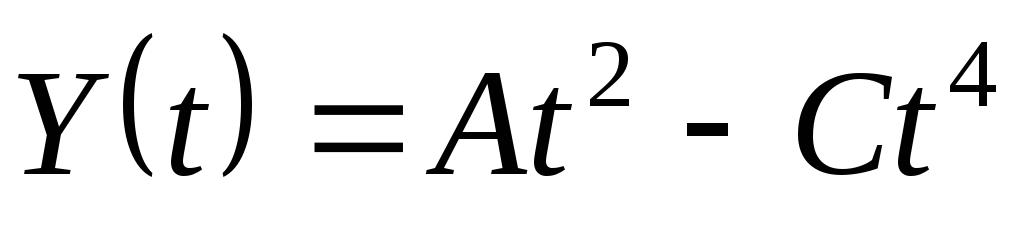 ,
где
,
где
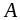 = 4.5 м/с2,
= 4.5 м/с2,
 = 0,25 м/с4 . Найти скорость и ускорение
точки в моменты времени t1
= 2 c и t2
= 4 с. Каковы средняя скорость перемещения
и средняя путевая скорость для промежутка
времени от 2 до 4с ?
= 0,25 м/с4 . Найти скорость и ускорение
точки в моменты времени t1
= 2 c и t2
= 4 с. Каковы средняя скорость перемещения
и средняя путевая скорость для промежутка
времени от 2 до 4с ? -
Материальная точка движется по окружности радиусом R = 4 м. Закон ее движения описывается уравнением
 ,
где
,
где
 = 8 м,
= 8 м,
 = 2 м/с2, а
= 2 м/с2, а
 отсчитывается вдоль окружности. Найти
момент времени, когда нормальное
ускорение точки равно 9 м/с2, а
также скорость, тангенциальное и полное
ускорения точки в этот момент времени.
отсчитывается вдоль окружности. Найти
момент времени, когда нормальное
ускорение точки равно 9 м/с2, а
также скорость, тангенциальное и полное
ускорения точки в этот момент времени. -
Вращение колеса задается уравнением
 ,
где
,
где
 = 3 рад,
= 3 рад,
 = 2 рад/с,
= 2 рад/с,
 = 1 рад/с3. Радиус колеса равен 1 м.
Для точки, лежащей на ободе колеса,
найти через t = 3 с после
начала движения угловую и линейную
скорости, угловое, тангенциальное и
нормальное ускорения.
= 1 рад/с3. Радиус колеса равен 1 м.
Для точки, лежащей на ободе колеса,
найти через t = 3 с после
начала движения угловую и линейную
скорости, угловое, тангенциальное и
нормальное ускорения. -
Тело движется по окружности радиусом 2 м. Закон его движения описывается уравнением
 (t)
= At
+ Bt3,
где А = 0,5 м/с, В = 0,1 м/с3,
а координата
(t)
= At
+ Bt3,
где А = 0,5 м/с, В = 0,1 м/с3,
а координата
 (t)
отсчитывается вдоль окружности. Найти
угловые скорость и ускорение в момент
t=2
с. Чему равно линейное ускорение тела
в указанный момент времени?
(t)
отсчитывается вдоль окружности. Найти
угловые скорость и ускорение в момент
t=2
с. Чему равно линейное ускорение тела
в указанный момент времени? -
Материальная точка движется по окружности радиусом
 м.
Зависимость угла поворота от времени
имеет вид
м.
Зависимость угла поворота от времени
имеет вид
 ,
где
,
где
 .
Определить линейное ускорение
материальной точки через секунду после
начала движения, а также угол между
линейным ускорением и радиусом окружности
в этот момент времени.
.
Определить линейное ускорение
материальной точки через секунду после
начала движения, а также угол между
линейным ускорением и радиусом окружности
в этот момент времени. -
Материальная точка движется по окружности радиуса R = 2 м. Закон ее движения описывается уравнением
 (t)
= At2
+ Bt3,
где А = 3 м/с2,
В = 1 м/с3,
а координата
(t)
= At2
+ Bt3,
где А = 3 м/с2,
В = 1 м/с3,
а координата
 (t)
отсчитывается вдоль окружности. Найти
момент времени, когда тангенциальное
ускорение точки равно 18 м/с2,
а также нормальное и полное линейное
ускорение точки в этот момент времени.
(t)
отсчитывается вдоль окружности. Найти
момент времени, когда тангенциальное
ускорение точки равно 18 м/с2,
а также нормальное и полное линейное
ускорение точки в этот момент времени. -
Н
 а
рисунке представлена зависимость
от времени проекции скорости тела на
ось
а
рисунке представлена зависимость
от времени проекции скорости тела на
ось
 (
( ).
Определить координату
).
Определить координату
 тела при
тела при
 ,
а также его среднюю скорость перемещения
и среднюю путевую скорость за промежуток
времени от 0 до 7 с, если в начальный
момент времени тело находилось в начале
координат.
,
а также его среднюю скорость перемещения
и среднюю путевую скорость за промежуток
времени от 0 до 7 с, если в начальный
момент времени тело находилось в начале
координат.
-
Т
 вердое
тело начинает вращаться вокруг оси
вердое
тело начинает вращаться вокруг оси
 с угловой скоростью, проекция которой
изменяется во времени, как показано на
графике. На какой угол (рад) относительно
начального положения окажется повернутым
тело через 10 секунд после начала
движения?
с угловой скоростью, проекция которой
изменяется во времени, как показано на
графике. На какой угол (рад) относительно
начального положения окажется повернутым
тело через 10 секунд после начала
движения?
-
В
 начальный момент времени (
начальный момент времени ( )
твердое тело, вращающееся вокруг оси
)
твердое тело, вращающееся вокруг оси
 ,
имеет проекцию угловой скорости
,
имеет проекцию угловой скорости
 .
Зависимость проекции углового ускорения
тела от времени показана на графике.
Определить угловую скорость тела в
момент времени
.
Зависимость проекции углового ускорения
тела от времени показана на графике.
Определить угловую скорость тела в
момент времени
 .
.
-

Два одинаковых груза массой 1 кг связаны нитью, перекинутой через невесомый блок (см. Рис.). Определить натяжение нити и коэффициент трения груза о плоскость стола, если ускорение грузов равно 4,5 м/с2. -
На шнуре, перекинутом через невесомый блок, уравновешены два груза массами по 2 кг каждое. С каким ускорением будут двигаться грузы, если на один из них положить небольшое тело массой 70 г? Каковы вес тела и сила натяжения шнура во время движения?
-
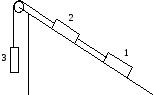
Три груза массами m1 = 100 г, m2 = 200 г и m3 = 300г связаны легкой нитью, перекинутой через невесомый блок, установленный на наклонной плоскости (см. Рис.). Угол наклона плоскости к горизонту равен 30°. Коэффициент трения между грузами и наклонной плоскостью равен 0,2. Определить ускорение грузов и натяжение нити, связывающей грузы 1 и 2. -

Через невесомый блок, укрепленный на ребре призмы, грани которой образуют углы 30° и 45° с горизонтом, перекинута нить (см. Рис.). К концам нити привязаны грузы массами по 1 кг каждый. Коэффициенты трения грузов о плоскость одинаковы и равны 0,1. Определить ускорение грузов и силу натяжения нити. -

Два бруска массами m1 = 1 кг и m2 = 2 кг, связанные нерастяжимой нитью, движутся по горизонтальной плоскости. К ним приложены силы F1 = 8 Н и F2 = 5 Н (см. Рис.), составляющие с горизонтом углы 30° и 45°. Коэффициенты трения брусков о плоскость одинаковы и равны 0,1. Система движется направо. Найти ускорение брусков и натяжение нити. -

Двое саней массой по 20 кг каждые, связанные между собой веревкой, тянут с силой 200 Н под углом 30 к горизонту. Найти ускорение саней и силу натяжения веревки, связывающей сани, если коэффициент трения полозьев о снег равен 0,025. -

Через невесомый блок перекинута нить, к концам которой подвешены три одинаковых груза массой m = 2 кг каждый. Найти ускорение системы и силу натяжения нити, связывающей грузы 1 и 2. -

На столе лежит деревянный брусок, к которому привязаны нити, перекинутые через невесомые блоки, укрепленные на обоих концах стола. К свободным концам нити подвешены грузы массами 0,85 кг и 0,2 кг, вследствие чего брусок приходит в движение и за 3 с проходит расстояние 0,81 м. Зная, что масса бруска 2 кг, определить коэффициент трения скольжения и силы натяжения нитей. -

Два груза массами m1 = 100 г и m2 = 200 г связаны нитью, перекинутой через невесомый блок, установленный на наклонной плоскости (см. Рис.). Угол наклона плоскости к горизонту равен 30°. Коэффициент трения между грузом и наклонной плоскостью равен 0,2. Определить ускорение грузов и натяжение нити. -

Три груза массами m1 = 200 г , m2 = 100 г и m3 = 300 г связаны легкой нитью, перекинутой через невесомый блок, установленный на наклонной плоскости (см. Рис.). Угол наклона плоскости к горизонту равен 45°. Коэффициент трения между грузом 1 и наклонной плоскостью равен 0,2. Определить ускорение грузов и натяжение нити, связывающей грузы 2 и 3. -
Самолет делает петлю в вертикальной плоскости. Определить вес летчика в верхней и нижней точках петли, если радиус петли 200 м, масса летчика 80 кг, скорость самолета 360 км/ч.
-
Груз, привязанный к нити, описывает в горизонтальной плоскости окружность радиусом 40 см. Нить образует с вертикалью угол 30о. Определить скорость груза.
-
На горизонтальной вращающейся платформе на расстоянии R = 0,8 м от оси вращения лежит груз. При какой угловой скорости вращения платформы груз начнет соскальзывать с нее, если коэффициент трения между грузом и платформой = 0,1?
-
В известном аттракционе “автомобиль на вертикальной стене” автомобиль движется по внутренней поверхности цилиндра в горизонтальной плоскости. Каков должен быть коэффициент трения между шинами и поверхностью цилиндра R = 5 м, чтобы автомобиль не сползал вниз при скорости v = 72 км/ч?
-
С какой максимальной скоростью может ехать мотоцикл по горизонтальной поверхности, описывая дугу радиусом 100 м, если коэффициент трения резины о почву = 0,4?
-
Камень массой 1 кг падает с высоты 20 м и в момент падения на землю имеет скорость 18 м/с. Определить работу силы сопротивления воздуха и величину этой силы, считая ее постоянной.
-

Тело массой 10 г падает с высоты 20 см на вертикально расположенную пружину, вызывая ее сжатие. Определить максимальное смещение верхнего конца пружины, если начальная высота пружины 10 см, а ее жесткость 100 Н/м. -
Из бесконечности на поверхность Земли падает метеорит массой m = 30 кг. Какая работа будет совершена при этом силами тяготения Земли? Считать известными ускорение свободного падения у поверхности Земли g = 9,8 м/с2 и радиус Земли R = 6400 км.
-
С поверхности Земли вертикально вверх пущена ракета со скоростью v = 8 км/с. На какую высоту она поднимется? Радиус Земли R = 6400 км, а ее масса М = 6 1024 кг.
-
Пружина жесткостью k = 500 Н/м сжата силой F = 100 Н. Определить работу внешней силы, дополнительно сжимающей эту пружину на l = 2 см.
-
С горки высотой 2 м съезжают санки. Какой путь пройдут санки по горизонтали, если коэффициент трения на горизонтальном пути равен 0.06? Трением на горке пренебречь
-
Мальчик массой 40 кг, скатившись на санках с горки высотой 2 м и углом наклона 300, проехал по горизонтальной дороге до остановки путь 20 м. Найти коэффициент трения, считая его постоянным на всём пути движения, и силу трения на горизонтальном участке.
-
Пуля массой 10 г подлетает к неподвижно закрепленной доске толщиной 4 см со скоростью 600 м/с и, пробив ее, вылетает со скоростью 400 м/с. Найти силу сопротивления доски, считая ее постоянной.
-
Т
 ело
массой m
соскальзывает без трения с некоторой
высоты по наклонной плоскости, переходящей
в петлю радиуса R
(рис.). Чему равна эта высота, если реакция
опоры в верхней точке петли (точка А)
равна силе тяжести mg,
действующей на тело?
ело
массой m
соскальзывает без трения с некоторой
высоты по наклонной плоскости, переходящей
в петлю радиуса R
(рис.). Чему равна эта высота, если реакция
опоры в верхней точке петли (точка А)
равна силе тяжести mg,
действующей на тело?
-
Автомобиль массой 2 т прошел по горизонтальной дороге при аварийном торможении путь 50 м. Найти работу силы трения и начальную скорость автомобиля, если коэффициент трения равен 0,4.
-
Т
 ело
массой m
соскальзывает без трения с высоты H=5R
по наклонной плоскости, переходящей в
петлю радиуса R
(рис.). Чему равна реакция опоры в нижней
точке петли?
ело
массой m
соскальзывает без трения с высоты H=5R
по наклонной плоскости, переходящей в
петлю радиуса R
(рис.). Чему равна реакция опоры в нижней
точке петли? -
Маятник массой 0,1 кг отклонили в горизонтальное положение и отпустили. Определить натяжение нити в момент, когда она составляет с вертикалью угол 60о.
-
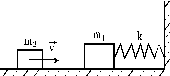 На
горизонтальном столе лежит тело массой
m1, соединенное с пружиной жесткостью
k. Второй конец пружины закреплен. В это
тело попадает тело массой m2,
движущееся со скоростью v. Определить
максимальную деформацию пружины, если
удар неупругий. Трением пренебречь.
На
горизонтальном столе лежит тело массой
m1, соединенное с пружиной жесткостью
k. Второй конец пружины закреплен. В это
тело попадает тело массой m2,
движущееся со скоростью v. Определить
максимальную деформацию пружины, если
удар неупругий. Трением пренебречь. -
Определить скорость пули массой m = 10 г, если при выстреле в ящик с песком массой М = 1 кг, висящий на подвесе длиной l = 1 м, он отклонился от вертикального положения на 90о (пуля застревает в песке).
-
Два шарика одинаковой массы подвешены на параллельных нитях одинаковой длины так, что они соприкасаются. Первый шар отклоняют так, что его центр масс поднимается на высоту 5 см, и отпускают. На какую высоту поднимутся шары после соударения, если удар неупругий?
-

Два тела массой кг и
кг и
 кг связаны нитью, перекинутой через
блок массой
кг связаны нитью, перекинутой через
блок массой
 кг (см. Рис.). Определить ускорение
тел, если коэффициент трения тела 1 о
плоскость стола
кг (см. Рис.). Определить ускорение
тел, если коэффициент трения тела 1 о
плоскость стола
 .
.
-


Через блок массой 1 кг, укрепленный на ребре призмы, грани которой образуют углы 30° и 45° с горизонтом, перекинута нить (см. Рис.). К концам нити привязаны грузы массами по 2 кг каждый. Коэффициенты трения грузов о плоскость одинаковы и равны 0,1. Определить ускорение грузов. -
Через блок массой 1 кг перекинута нить, к концам которой подвешены три одинаковых груза массой m = 2 кг каждый. Найти ускорение системы и силу натяжения нити, связывающей грузы 1 и 2.
-

Два груза массами m1 = 100 г и m2 = 200 г связаны нитью, перекинутой через блок массой m=100 г, установленный на наклонной плоскости (см. Рис.). Угол наклона плоскости к горизонту равен 30°. Коэффициент трения между грузом и наклонной плоскостью равен 0,2. Определить ускорение грузов. -
К
 грузу 3, масса которого
грузу 3, масса которого
 кг,
нитью, перекинутой через блок массой
кг,
нитью, перекинутой через блок массой
 кг, привязаны два груза массой
кг, привязаны два груза массой
 кг
(см. Рис). Определить ускорение грузов.
Трением груза 3 о плоскость стола
пренебречь.
кг
(см. Рис). Определить ускорение грузов.
Трением груза 3 о плоскость стола
пренебречь. -
Н
 а
шнуре, перекинутом через блок массой
0.5 кг, уравновешены два груза массой по
1 кг каждый. С каким ускорением будут
двигаться грузы, если на один из них
положить небольшое тело массой 100 г?
Каков вес тела во время движения?
а
шнуре, перекинутом через блок массой
0.5 кг, уравновешены два груза массой по
1 кг каждый. С каким ускорением будут
двигаться грузы, если на один из них
положить небольшое тело массой 100 г?
Каков вес тела во время движения? -
О

 пределить
натяжения нити, связывающей первый и
второй грузы (см. рис), если масса первого
груза равна 0,5 кг, второго – 0,3 кг,
третьего – 2 кг, а масса блока – 1 кг.
Трением грузов о поверхность пренебречь.
пределить
натяжения нити, связывающей первый и
второй грузы (см. рис), если масса первого
груза равна 0,5 кг, второго – 0,3 кг,
третьего – 2 кг, а масса блока – 1 кг.
Трением грузов о поверхность пренебречь.
-
Два груза массами m1 = 1 кг и m2 = 4 кг, связанные нитью, перекинутой через блок массой m= 0.5 кг, движутся по горизонтальной и наклонной (
 )
поверхностям. Найти ускорение грузов,
если коэффициент трения между ними и
поверхностями
= 0,1.
)
поверхностям. Найти ускорение грузов,
если коэффициент трения между ними и
поверхностями
= 0,1. -
О

 днородный
шар массой
днородный
шар массой
 кг
может вращаться вокруг вертикальной
оси, проходящей через его центр. На
"экватор" шара намотана нить,
другой конец которой, перекинутый через
цилиндрический блок массой
кг
может вращаться вокруг вертикальной
оси, проходящей через его центр. На
"экватор" шара намотана нить,
другой конец которой, перекинутый через
цилиндрический блок массой
 кг, привязан к грузу массой
кг, привязан к грузу массой
 кг. Определить ускорение груза, если
блок и шар вращаются без трения.
кг. Определить ускорение груза, если
блок и шар вращаются без трения.
-
О
 днородный
цилиндр массой
днородный
цилиндр массой
 кг может вращаться вокруг вертикальной
оси. На цилиндр намотана нить, другой
конец которой, перекинутый через
цилиндрический блок массой
кг может вращаться вокруг вертикальной
оси. На цилиндр намотана нить, другой
конец которой, перекинутый через
цилиндрический блок массой
 кг, привязан к грузу массой
кг, привязан к грузу массой
 кг. Определить ускорение груза, если
блок и цилиндр вращаются без трения.
кг. Определить ускорение груза, если
блок и цилиндр вращаются без трения.
-
На однородный сплошной цилиндр радиуса
 м и массы
м и массы
 кг, который
может вращаться вокруг оси, совпадающей
с его осью симметрии (ось z),
намотана нить. За нить тянут так, что
зависимость угла поворота цилиндра от
времени имеет вид
кг, который
может вращаться вокруг оси, совпадающей
с его осью симметрии (ось z),
намотана нить. За нить тянут так, что
зависимость угла поворота цилиндра от
времени имеет вид
 ,
где
,
где
 .
Определить
силу натяжения нити через две секунды
после начала вращения цилиндра, если
со стороны оси на вращающийся
цилиндр
действует постоянный тормозящий момент,
величина которого
.
Определить
силу натяжения нити через две секунды
после начала вращения цилиндра, если
со стороны оси на вращающийся
цилиндр
действует постоянный тормозящий момент,
величина которого
 .
.
-
О
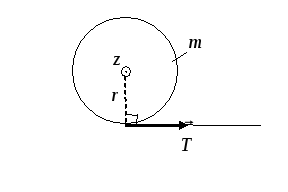 днородный
шар радиуса
днородный
шар радиуса
 м и массы
м и массы
 кг может
вращаться вокруг оси z,
проходящей через его центр. На "экватор"
шара намотана нить, за которую тянут
так, что зависимость угла поворота шара
от времени имеет вид
кг может
вращаться вокруг оси z,
проходящей через его центр. На "экватор"
шара намотана нить, за которую тянут
так, что зависимость угла поворота шара
от времени имеет вид
 ,
где
,
где
 .
Определить
силу натяжения нити через две секунды
после начала вращения шара, если со
стороны оси на вращающийся шар действует
постоянный тормозящий момент, величина
которого
.
Определить
силу натяжения нити через две секунды
после начала вращения шара, если со
стороны оси на вращающийся шар действует
постоянный тормозящий момент, величина
которого
 .
.
-
М
 аятник
(в виде буквы Т) изготовлен из двух
однородных стержней длиной
аятник
(в виде буквы Т) изготовлен из двух
однородных стержней длиной
 и массой
и массой
 .
Он колеблется вокруг горизонтальной
оси, проходящей на расстоянии
.
Он колеблется вокруг горизонтальной
оси, проходящей на расстоянии
 от конца одного из стержней (точка О).
Определить момент силы тяжести
относительно точки О и угловое ускорение
маятника в момент времени, когда он
отклонен из положения равновесия на
900.
Считать, что маятник вращается без
трения.
от конца одного из стержней (точка О).
Определить момент силы тяжести
относительно точки О и угловое ускорение
маятника в момент времени, когда он
отклонен из положения равновесия на
900.
Считать, что маятник вращается без
трения.
-
М

 аятник
(в виде буквы Т) изготовлен из двух
однородных стержней длиной
аятник
(в виде буквы Т) изготовлен из двух
однородных стержней длиной
 и массой
и массой
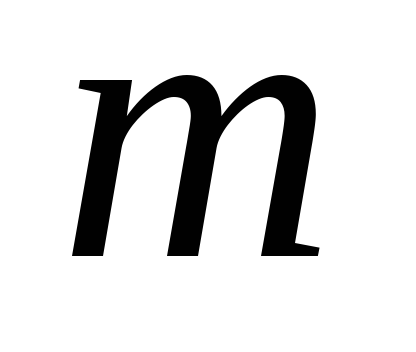 .
Он колеблется вокруг горизонтальной
оси, проходящей через конец одного из
стержней (точка О). Определить момент
силы тяжести относительно точки О и
угловое ускорение маятника в момент
времени, когда он отклонен из положения
равновесия на 900.
Считать, что маятник вращается без
трения.
.
Он колеблется вокруг горизонтальной
оси, проходящей через конец одного из
стержней (точка О). Определить момент
силы тяжести относительно точки О и
угловое ускорение маятника в момент
времени, когда он отклонен из положения
равновесия на 900.
Считать, что маятник вращается без
трения.
-
Маятник (в виде буквы Т) изготовлен из двух однородных стержней длиной
 и массой
и массой
 .
Он колеблется вокруг горизонтальной
оси, проходящей через середину одного
из стержней (точка О). Определить момент
силы тяжести относительно точки О и
угловое ускорение маятника в момент
времени, когда он отклонен из положения
равновесия на 300.
Считать, что маятник вращается без
трения.
.
Он колеблется вокруг горизонтальной
оси, проходящей через середину одного
из стержней (точка О). Определить момент
силы тяжести относительно точки О и
угловое ускорение маятника в момент
времени, когда он отклонен из положения
равновесия на 300.
Считать, что маятник вращается без
трения.
-
Сплошной однородный цилиндр радиусом r = 10 см и массой m =2 кг скатывается без проскальзывания с высоты 1 м вдоль наклонной плоскости. Определите момент импульса цилиндра относительно оси вращения у основания наклонной плоскости.
-
Однородный сплошной цилиндр и однородный шар, имеющие одинаковую массу и радиус, закатываются без проскальзывания на наклонную плоскость. Найти отношение высот, на которые они поднимутся вдоль наклонной плоскости, если у основания наклонной плоскости их скорости одинаковы.
-
Однородный сплошной цилиндр и однородный шар, имеющие одинаковую массу и радиус, скатываются с одинаковой высоты вдоль наклонной плоскости. Найти отношение их скоростей у основания наклонной плоскости.
-
Полый цилиндр и однородный шар, имеющие одинаковую массу и радиус, скатываются с одинаковой высоты вдоль наклонной плоскости. Найти отношение их скоростей у основания наклонной плоскости.
-
Полый и однородный сплошной цилиндры, имеющие одинаковую массу и радиус, скатываются с одинаковой высоты вдоль наклонной плоскости. Найти отношение их скоростей у основания наклонной плоскости.
-
М
 аховик
в виде сплошного однородного цилиндра
массой 2 кг и радиусом 20 см, вращаясь
равнозамедленно, уменьшил частоту
своего вращения с 480 об/мин до 120 об/мин
и, при этом, сделал 40 оборотов. Определите
работу торможения и тормозящий момент.
аховик
в виде сплошного однородного цилиндра
массой 2 кг и радиусом 20 см, вращаясь
равнозамедленно, уменьшил частоту
своего вращения с 480 об/мин до 120 об/мин
и, при этом, сделал 40 оборотов. Определите
работу торможения и тормозящий момент. -
Стержень длиной
 м
и массой
м
и массой
 кг
может вращаться вокруг горизонтальной
оси, проходящей на расстоянии
кг
может вращаться вокруг горизонтальной
оси, проходящей на расстоянии
 от его верхнего конца (точка О). Его
отклонили из положения равновесия на
угол 900 и отпустили. Определить
постоянный момент силы трения, который
ось прикладывает к стержню, если при
прохождении положения равновесия
угловая скорость стержня
от его верхнего конца (точка О). Его
отклонили из положения равновесия на
угол 900 и отпустили. Определить
постоянный момент силы трения, который
ось прикладывает к стержню, если при
прохождении положения равновесия
угловая скорость стержня
 рад/с.
рад/с.
-
О
 бруч
радиусом
бруч
радиусом
 м
и массой
м
и массой
 кг
может вращаться вокруг горизонтальной
оси (точка О). Его отклонили из положения
равновесия на угол 900 и отпустили.
Определить постоянный момент силы
трения, который ось прикладывает к
обручу, если при прохождении положения
равновесия угловая скорость обруча
кг
может вращаться вокруг горизонтальной
оси (точка О). Его отклонили из положения
равновесия на угол 900 и отпустили.
Определить постоянный момент силы
трения, который ось прикладывает к
обручу, если при прохождении положения
равновесия угловая скорость обруча
 рад/с.
рад/с.
-
О
 днородный
сплошной цилиндр радиусом
днородный
сплошной цилиндр радиусом
 м
и массой
м
и массой
 кг
может вращаться вокруг горизонтальной
оси (точка О). Его отклонили из положения
равновесия на угол 900 и отпустили.
Определить постоянный момент силы
трения, который ось прикладывает к
цилиндру, если при прохождении положения
равновесия угловая скорость цилиндра
кг
может вращаться вокруг горизонтальной
оси (точка О). Его отклонили из положения
равновесия на угол 900 и отпустили.
Определить постоянный момент силы
трения, который ось прикладывает к
цилиндру, если при прохождении положения
равновесия угловая скорость цилиндра
 рад/с.
рад/с.
-
О
 днородный
шар катится без проскальзывания по
горке. Зависимость его потенциальной
энергии от координаты
днородный
шар катится без проскальзывания по
горке. Зависимость его потенциальной
энергии от координаты
 изображена на графике. Чему равна
кинетическая энергия шара, обусловленная
вращением, в точке «Б», если в точке «А»
его полная кинет
изображена на графике. Чему равна
кинетическая энергия шара, обусловленная
вращением, в точке «Б», если в точке «А»
его полная кинет ическая
энергия равна 10 Дж.
ическая
энергия равна 10 Дж. -
Однородный сплошной цилиндр катится без проскальзывания по горке. Зависимость его потенциальной энергии от координаты
 изображена на графике. Определить
кинетическую энергию цилиндра,
обусловленную движением его центра
масс, в точке «С», если в точке «А» полная
кинетическая энергия цилиндра равна
20 Дж.
изображена на графике. Определить
кинетическую энергию цилиндра,
обусловленную движением его центра
масс, в точке «С», если в точке «А» полная
кинетическая энергия цилиндра равна
20 Дж.
-
П
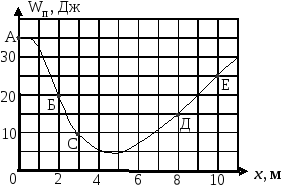 олый
цилиндр катится без проскальзывания
по горке. Зависимость его потенциальной
энергии от координаты
олый
цилиндр катится без проскальзывания
по горке. Зависимость его потенциальной
энергии от координаты
 изображена на графике. Определить
кинетическую энергию цилиндра,
обусловленную вращением, в точке «Е»,
если в точке «А» его скорость равнялась
нулю.
изображена на графике. Определить
кинетическую энергию цилиндра,
обусловленную вращением, в точке «Е»,
если в точке «А» его скорость равнялась
нулю.
-
П
 олый
цилиндр катится без проскальзывания
по горке. Зависимость его потенциальной
энергии от координаты
олый
цилиндр катится без проскальзывания
по горке. Зависимость его потенциальной
энергии от координаты
 изображена на графике. Определить
кинетическую энергию цилиндра,
обусловленную движением его центра
масс, в точке «С», если в точке «А» полная
кинетическая энергия цилиндра равна
30 Дж.
изображена на графике. Определить
кинетическую энергию цилиндра,
обусловленную движением его центра
масс, в точке «С», если в точке «А» полная
кинетическая энергия цилиндра равна
30 Дж. -
О
 днородный
шар катится без проскальзывания по
горке. Зависимость его потенциальной
энергии от координаты
днородный
шар катится без проскальзывания по
горке. Зависимость его потенциальной
энергии от координаты
 изображена на графике. Определить
кинетическую энергию шара, обусловленную
движением его центра масс, в точке «Д»,
если в точке «А» полная кинетическая
энергия шара равна 10 Дж.
изображена на графике. Определить
кинетическую энергию шара, обусловленную
движением его центра масс, в точке «Д»,
если в точке «А» полная кинетическая
энергия шара равна 10 Дж.
-
О
 днородный
сплошной цилиндр катится без
проскальзывания по горке. Зависимость
его потенциальной энергии от координаты
днородный
сплошной цилиндр катится без
проскальзывания по горке. Зависимость
его потенциальной энергии от координаты
 изображена на графике. Определить
кинетическую энергию цилиндра,
обусловленную вращением, в точке «К»,
если в точке «А» его полная кинетическая
энергия равна 30 Дж.
изображена на графике. Определить
кинетическую энергию цилиндра,
обусловленную вращением, в точке «К»,
если в точке «А» его полная кинетическая
энергия равна 30 Дж.
-
С какой скоростью должна двигаться частица, чтобы ее кинетическая энергия равнялась удвоенной энергии покоя?
-
Собственное время жизни частицы равно
 с.
Определить время жизни этой частицы в
системе отсчета, относительно которой
она движется со скоростью
с.
Определить время жизни этой частицы в
системе отсчета, относительно которой
она движется со скоростью
 .
(
.
( --
скорость света).
--
скорость света). -
С какой скоростью должна двигаться частица, чтобы ее полная энергия в 5 раз превышала ее энергию покоя?
-
Относительно неподвижной системы отсчета навстречу друг другу движутся две частицы с одинаковой скоростью , равной 0,4с (с – скорость света). С какой скоростью движется одна частица относительно другой?
-
Во сколько раз изменится полная энергия частицы, если ее скорость увеличится с 0,5с до 0,9с? (с – скорость света)?
-
Во сколько раз изменится кинетическая энергия частицы, если ее скорость увеличится с 0,3с до 0,8с? (с – скорость света)?
-
С какой скоростью должна двигаться частица, чтобы ее кинетическая энергия увеличилась в 2 раза, если сначала скорость её была
 с
(с – скорость света)?
с
(с – скорость света)? -
С какой скоростью должна двигаться частица, чтобы ее полная энергия увеличилась в 3 раза, если сначала скорость её была
 с
(с – скорость света)?
с
(с – скорость света)? -
Над первоначально покоившейся частицей массой
 была совершена работа
была совершена работа
 (с – скорость света). Определить ее
импульс.
(с – скорость света). Определить ее
импульс.
-
Над частицей массой
 ,
двигавшейся со скоростью
,
двигавшейся со скоростью
 ,
была совершена работа
,
была совершена работа
 (с – скорость света). Определить ее
конечный импульс.
(с – скорость света). Определить ее
конечный импульс. -
С какой скоростью должен двигаться стержень, чтобы его релятивистское сокращение составило 1/3 его собственной длины?
-
Скорость движения стержня в направлении его оси равна 0,8с. На сколько процентов сократилась его длина?
-
Две одинаковые частицы массой
 движутся навстречу друг другу с
одинаковыми скоростями
движутся навстречу друг другу с
одинаковыми скоростями
 (с – скорость света). Определить массу
частицы, образовавшейся в результате
их абсолютно неупругого столкновения.
(с – скорость света). Определить массу
частицы, образовавшейся в результате
их абсолютно неупругого столкновения.
-
Неподвижная частица массой
 распадается на две одинаковые частицы
массой
распадается на две одинаковые частицы
массой
 каждая. Найти скорость этих частиц.
каждая. Найти скорость этих частиц.
-
Неподвижная частица массой
 распадается на две одинаковые частицы,
движущиеся со скоростью
распадается на две одинаковые частицы,
движущиеся со скоростью
 каждая (с – скорость света). Определить
массу образовавшейся частицы.
каждая (с – скорость света). Определить
массу образовавшейся частицы.
