5.2. Характеристики цикла. Виды циклов

На рис.5.2 приведён график напряжений при наиболее распространённом симметричном цикле. Если к вращающемуся валу приложить дополнительную продольную силу постоянной величины, то к напряжениям (5.2) добавится постоянное напряжение и напряжения будут меняться по закону, изображённому на рис.5.4. Такой закон изменения напряжений носит название асимметричного цикла. Асимметричный цикл может быть знакопостоянным и знакопеременным. На рис.5.4 – знакопостоянный цикл.

На усталостную прочность в основном влияют максимальные σ_max и минимальные σ_min напряжения цикла. Эти величины являются исходными для расчёта других характеристик цикла.

Рис. 5.4

Среднее (постоянное) напряжение цикла (рис.5.4):

. (5.3)

Амплитуда цикла (рис.13.4):

. (5.4)

Среднее напряжение может быть как положительным, так и отрицательным, амплитуда же цикла определяется абсолютной величиной (без учёта знака).

Коэффициент асимметрии цикла – это отношение минимального напряжения цикла к максимальному с учётом знаков этих напряжений, обозначается буквой r:

. (5.5)

Определитель цикла – это отношение амплитуды к среднему напряжению. На диаграмме предельных напряжений, которая будет рассмотрена ниже, определитель цикла представляет собой тангенс угла наклона прямой, проведённой из начала координат, к оси абсцисс. Из формул (5.3)  (5.5) определитель цикла равен

. (5.6)

Циклы, имеющие одинаковые коэффициенты асимметрии r, называются подобными.

При расчёте деталей машин могут встретиться любые виды циклов напряжений. Остановимся лишь на самых характерных, наиболее часто встречающихся.

Симметричный цикл. Это, безусловно, самый распространённый цикл переменных напряжений (рис.5.2). Его характеристики:

σ_max = – σ_min, σ_с = 0, σ_a = σ_max, r = – 1, tg γ = ∞.

Симметричный цикл является наиболее опасным, при любой деформации прочность самая низкая.

Пульсирующий или отнулевой цикл. Второй после симметричного по распространённости, график – на рис.5.5. Характеристики:

σ_max > 0, σ_min,= 0, σ_с = 0,5σ_max, σ_a = 0,5σ_max, r = 0, tg γ = 1.

Статическое напряжение. Оно может рассматриваться как частный случай циклического (рис.5.6).

Характеристики:

σ_max = σ_min > 0, σ_с = σ_max, σ_a = 0, r = + 1, tg γ = 0.

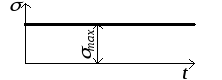
Рис. 5.5 Рис. 5.6

В заключение заметим, что во всех приведённых выше формулах и графиках фигурирует нормальное напряжение σ, т.е. идёт речь о циклическом растяжении–сжатии или изгибе. В случае циклического кручения букваσдолжна быть заменена на буквуτпри сохранении соответствующих индексов.

5.3. Экспериментальное определение характеристик сопротивления усталости

Как отмечалось выше, усталостная прочность (выносливость) деталей зависит от числа циклов до разрушения. Надо иметь в виду, что не любые по величине переменные напряжения вызывают усталостное разрушение. Оно может наступить при условии, если переменные напряжения в той или иной точке детали превзойдут своё критическое значение, называемое пределом выносливости.

Предел выносливости – это наибольшее значение максимального напряжения цикла σ_max, которое не вызывает усталостного разрушения при неограниченно большом числе циклов.

Предел выносливости – обозначается σ_r, где r – коэффициент асимметрии цикла. При симметричном цикле предел выносливости обозначается σ_-1, при пульсирующем – σ₀. Чтобы определить предел выносливости, необходимо построить кривую усталости (кривую Веллера) в координатах σ – N или σ – lg N или lg σ – lg N. Для построения кривой надо испытать 6  10 образцов.

При симметричном цикле предел выносливости σ_-1 меньше, чем предел выносливости других видов циклов, а определение его значительно проще. Пределы выносливости при выбранной характеристики цикла r, разумеется, будут различными в зависимости от вида деформации, при которой испытываются образцы.

Рис.5.7

Самая простая испытательная машина для определения предела выносливости при изгибе показана на рис.5.7. Цилиндрический полированный образец 4 диаметром от7  10 мм зажимается в захвате 3. На свободном конце образца через подшипник 5 подвешивается груз 6. Образец вращается электромотором 1, один оборот – один цикл. После разрушения образца груз падает и нажимает на кнопку 7, которая выключает мотор. Счётчик оборотов 2 показывает число циклов до разрушения N.

Порядок установления нагрузок на испытываемые образцы в большинстве случаев принимают ниспадающим, т.е. на первый образец дают нагрузку, напряжение при которой значительно превышает предел выносливости, а нагрузку на последующие образцы постепенно снижают. Разумеется, каждый из менее нагруженных образцов будет выдерживать всё большее и большее число циклов. По точкам разрушившихся образцов строят кривую усталости (рис.5.8).

а б

Рис.5.8

Кривая усталости σ = f (N)(кривая Веллера) на рис.5.8,а асимптотически приближается к горизонтальной прямой, ординатой которой и определяется предел выносливости.

Испытания чёрных металлов показали, что если образец не разрушается после 10⁷ оборотов, то он не разрушается вообще. Поэтому испытания образцов из чёрных металлов прекращают после 10⁷ циклов – «базы испытания». Базой испытания на выносливость называется наименьшее число циклов, существенное превышение которого не приведёт к усталостному разрушению образца. Для цветных металлов база испытания принята равной 10⁸ циклов, т.к. кривая не имеет асимптоты.

В связи с тем, что по кривой усталости в координатах N – σ часто бывает затруднительно определить положение асимптоты, кривую строят в полулогарифмических (рис.5.8,б) или логарифмических координатах. Предел выносливости определяется по перелому кривой.

Многочисленные экспериментальные данные позволили установить некоторые соотношения между пределами выносливости при различных видах деформации, и в частности, между пределами выносливости при изгибе , крученииτ_-1 и растяжении–сжатии при симметричном цикле. Эти соотношения приблизительно следующие:

для стали ;

; (5.7)

для чугуна ;

.

Кроме того, установлены некоторые соотношения между пределами выносливости и основной механической характеристикой прочности при статической нагрузке – пределом прочности σ_ПЧ:

для стали

; (5.8)

τ_-1 = 0,22 σ_ПЧ;

для высокопрочных сталей .

Следует отметить, что формулы (5.7) и (5.8) – сугубо приближенные и могут быть использованы только для ориентировочных расчётов в случае отсутствия данных о пределе выносливости.

Из сказанного выше ясно, что определение основной характеристики прочности при цикличных напряжениях – предела выносливости – требует проведения трудоёмких длительных экспериментов, для которых нужны специальные испытательные машины. Если для испытаний на изгиб при асимметричном цикле применяют простые машины типа той, которая схематически показана на рис.5.7, то для испытаний на осевое действие нагрузки или кручение при симметричном и произвольном асимметричном циклах нужны сложные машины с гидравлическим приводом (пульсаторы).

Чтобы охарактеризовать сопротивляемость материала действию переменных напряжений с различной асимметрией цикла, по результатам испытаний строят так называемую диаграмму предельных напряжений. На рис.5.9 представлена диаграмма Хея: по оси абсцисс откладывают среднее напряжение цикла σ_с, а по оси ординат – амплитуда цикла σ_а. Возможен другой вариант – диаграмма Смита: по оси абсцисс откладывают тоже σ_с, а по оси ординат – наибольшее σ_max и наименьшее σ_min напряжения цикла.

Основные точки диаграммы Хея (рис.5.9): точка А соответствует симметричному циклу – σ_с = 0, σ_а = σ_-1; точка В соответствует статическому нагружению – σ_а = 0, σ_с = σ₊₁ = σ_ПЧ; точка C соответствует пульсирующему циклу ,.

Рис.5.9

Прямая, проведённая из начала координат под углом γк оси абсцисс, позволяет найти предел выносливости для произвольного асимметричного цикла. Определитель цикла находится по формуле (5.6)

, , .

На луче надо найти точку, соответствующую напряжению в детали, – точку M₁. После чего можно определить коэффициент запаса прочности

. (5.9)