
- •Типовой расчет «Математический анализ» з а д а ч а 1
- •Контрольные варианты к задаче 1
- •Контрольные варианты к задаче 7
- •З а д а ч а 8
- •Контрольные варианты к задаче 8
- •З а д а ч а 9
- •Контрольные варианты к задаче 9
- •З а д а ч а 10
- •Контрольные варианты к задаче 10
- •З а д а ч а 11
- •З а д а ч а 14
- •Контрольные варианты задачи 14
Типовой расчет «Математический анализ» з а д а ч а 1
Правило 1.
Чтобы вычислить
 ,
нужно вместо переменной х поставить
её предельное значение
,
нужно вместо переменной х поставить
её предельное значение![]() .
.
Если
 то
то![]()
Если
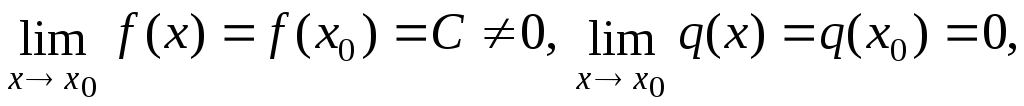 то
то![]() .
.
Если
 то
то![]() - неопределенность.
- неопределенность.
Правило 2.
Чтобы раскрыть
неопределенность
![]() в алгебраическом выражении, надо в
числителе и знаменателе выделить
множитель
в алгебраическом выражении, надо в
числителе и знаменателе выделить
множитель![]() ,
который стремится к нулю, и на него под
знаком предела сократить.
,
который стремится к нулю, и на него под
знаком предела сократить.
Правило 3.
Если в
числителе и знаменателе стоят многочлены,
то чтобы получить множитель
![]() ,
нужно многочлены разложить на множители.
,
нужно многочлены разложить на множители.
Пример 1
При решении этой задачи необходимо знать формулы:
![]()
Вычислить
предел
![]() .Действительно:
.Действительно:
![]() .
.
Найдем корни
многочлена
![]() по формуле
по формуле![]() .
.
Тогда
![]()
![]()
![]() .
.
Анологично
![]() т.е
т.е
![]() .
.

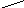
![]()
Контрольные варианты к задаче 1
Вычислить пределы функции:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
З а д а ч а 2
При решении этой задачи необходимо знать формулы:
![]()
![]() .
.
Пример 2
Вычислить
![]()
Найдем корни
многочлена по формуле
![]() .
.
Тогда
![]() и
и
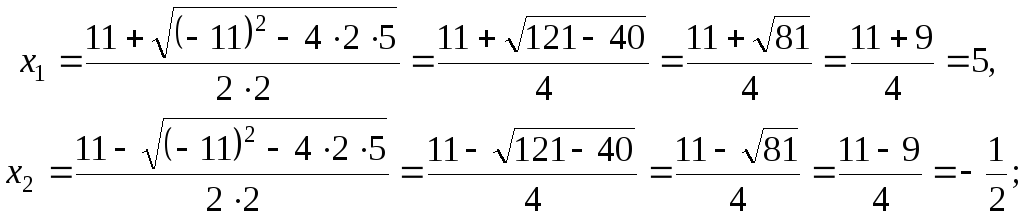
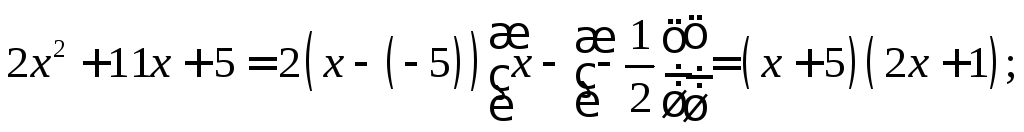
По формуле :
![]() имеем
имеем
![]()
![]()


![]()
Контрольные варианты к задаче 2
Вычислить пределы функций:
|
1. |
2. |
|
3. |
4.
|
|
5.
|
6. |
|
7. |
8.
|
|
9. |
10.
|
|
11. |
12.
|
|
13. |
14.
|
|
15. |
16.
|
|
17. |
18. |
|
|
20.
|
|
21. |
22.
|
|
23.
|
24.
|
|
25. |
26.
|
|
27.
|
28.
|
|
29.
|
30.
|
З а д а ч а 3
Если при
![]()
![]() и
и![]() ,то отношение
,то отношение
![]() представляет собой неопределенность
представляет собой неопределенность![]() .
В этом случае рекомендуется числитель
и знаменатель разделить почленно на
старшую степень переменной х. При этом
необходимо знать , что величина обратная
бесконечно большой является
бесконечно
малой
.
В этом случае рекомендуется числитель
и знаменатель разделить почленно на
старшую степень переменной х. При этом
необходимо знать , что величина обратная
бесконечно большой является
бесконечно
малой
 Величина обратная бесконечно малой
является бесконечно большой
Величина обратная бесконечно малой
является бесконечно большой
Пример 3
Вычислить
предел
![]() .
.
 .
.
Контрольные варианты к задаче 3
Вычислить пределы функций:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
З а д а ч а 4
Если при
![]()
![]() и
и![]() ,
то отношение
,
то отношение![]() представляет собой неопределенность
представляет собой неопределенность![]() .
В этом случае рекомендуется числитель
и знаменатель разделить почленно на
старшую степень переменной х.
.
В этом случае рекомендуется числитель
и знаменатель разделить почленно на
старшую степень переменной х.
Пример 4
Вычислить
предел
![]() .
.
 .
.
Контрольные варианты к задаче 4
Вычислить пределы функций:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
З а д а ч а 5
При решении этой задачи необходимо знать формулы:
![]()
Пример 5
Вычислить
предел
![]() .
.
![]()
![]()
Здесь старшая
степень при n
– вторая и
![]() -
степень, поэтому
-
степень, поэтому

Контрольные варианты к задаче 5
Вычислить пределы числовых последовательностей:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
З а д а ч а 6
Если при
![]() и
и![]() ,
то разность
,
то разность![]() представляет
собой неопределенность
представляет
собой неопределенность![]() .
Чтобы раскрыть такую неопределенность,
надо привести её к виду
.
Чтобы раскрыть такую неопределенность,
надо привести её к виду![]() или
или![]() .
.
Пример 6
Вычислить
предел
![]() .
.
Умножим и разделим
на сопряженное выражение
![]() ,
тогда
,
тогда

Здесь старшая
степень
![]() -
первая, поэтому
-
первая, поэтому
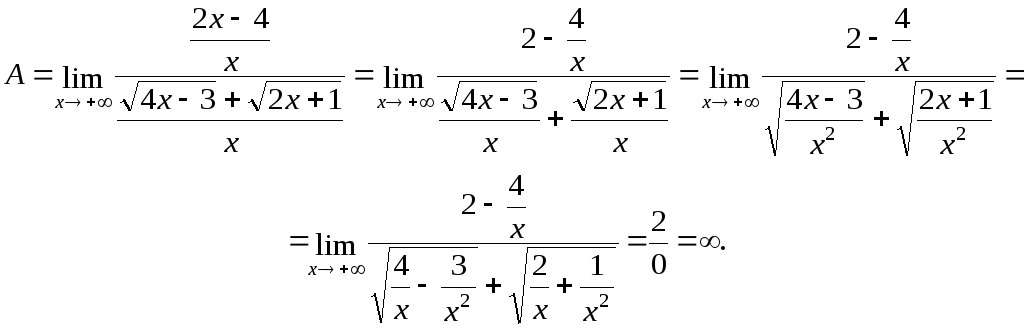
Контрольные варианты к задаче 6
Вычислить пределы функции:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
З а д а ч а 7
Две бесконечно
малые функции
![]() при
при![]() или
или![]() называются эквивалентными, если предел
их отношения равен единице. Эквивалентность
бесконечно малых функций записывается
в виде
называются эквивалентными, если предел
их отношения равен единице. Эквивалентность
бесконечно малых функций записывается
в виде![]() ~
~![]() .
.
Таким образом,
если
![]() ,
то
,
то![]() ~
~![]() .
.
Таблица эквивалентных бесконечно малых функций
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема.
Предел отношения двух бесконечно малых
не изменится, если одну или обе бесконечно
малые заменить им эквивалентными, т. е.
если
![]() ~
~![]() и
и![]() ~
~![]() ,
то
,
то
Заметим, что с
помощью эквивалентных бесконечно малых
раскрывают неопределенность
![]()
Пример 7
Вычислить
предел
![]()
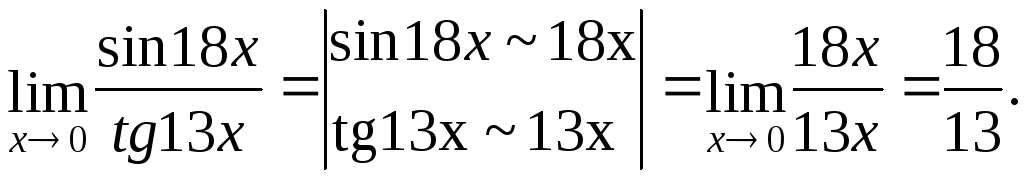
Пример 8
Вычислить
предел
![]()

Пример 9
Вычислить
предел
![]()


 ~
~
 ~
~