
- •Дискретная математика
- •5B0704 – Вычислительная техника и программное обеспечение,
- •5B0703 – Информационные системы
- •Isbn – 601 – 7098 – 78 - 0
- •1 Элементы теории множеств.
- •1.1 Множества
- •1.2 Отношения
- •1.3 Понятие о мощности множеств
- •2 Элементы математической логики
- •2.1 Высказывания и логические операции
- •2.2 Функции алгебры логики
- •2.3 Дизъюнктивные и конъюнктивные нормальные формы
- •2.4 Булева алгебра и теория множеств. Коммутационные схемы
- •3 Элементы теории графов
- •3.1 Основные понятия и определения
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН
Некоммерческое акционерное общество
«Алматинский университет энергетики и связи»
Кафедра высшей математики
Л.Н. Астраханцева
Дискретная математика
Учебное пособие
для студентов всех форм обучения специальностей
5B0704 – Вычислительная техника и программное обеспечение,
5B0703 – Информационные системы
Алматы 2011
УДК 519.6 (075.8)
ББК 22.176 Я 73
А 91 Дискретная математика:
Учебное пособие /Л.Н. Астраханцева;
АУЭС. Алматы, 2011.- 78 с.
Isbn – 601 – 7098 – 78 - 0
Пособие представляет собой переработанные и дополненные лекции по дискретной математике, читаемые автором в АУЭС, оно включает четыре раздела, традиционно изучаемые в курсе дискретной математики: элементы теории множеств и отношений, элементы математической логики, теории графов и комбинаторики. Содержание разделов взаимно связано друг с другом. В доступной форме изложены основные теоретические сведения, приведены примеры и решённые задачи, помогающие усвоить и закрепить изучаемый материал. Пособие предназначено для студентов всех форм обучения специальностей 5В070400 – Вычислительная техника и программное обеспечение и 5В070300 – Информационные системы.
Ил. 72, табл. 14, библиогр. – 16 назв.
![]()
ББК 22.176 Я 73
РЕЦЕНЗЕНТ: КазНУ, канд. физ.-мат. наук, доц. У.К. Койлышов.
АУЭС, канд. физ.-мат. наук, доц. М.Ж. Байсалова.
Печатается по плану издания Министерства образования и науки Республики Казахстан на 2011г.
© НАО «Алматинский университет энергетики и связи», 2011г.
1 Элементы теории множеств.
1.1 Множества
Понятия
множества и элемента множества являются
первичными (т.е. не определяемыми с
помощью других, более простых понятий)
такими, как, например, точка и прямая.
Под множеством понимается совокупность
некоторых объектов (предметов), которые
называются элементами множества.
Элементы множеств различны. Приняты
следующие обозначения: A,
B,
X,…
- множества; a,
b,
x,
x1,
x2,…-
элементы множеств;![]() -
элемент
-
элемент![]() принадлежит
А,
принадлежит
А,![]() -
элемент
-
элемент![]() не
принадлежит А;N
– множество натуральных чисел; Z
– множество целых чисел; Q
– множество рациональных чисел; I
- множество иррациональных чисел; R
– множество действительных чисел; C
– множество комплексных чисел; Ø –
пустое множество (не содержит ни одного
элемента).
не
принадлежит А;N
– множество натуральных чисел; Z
– множество целых чисел; Q
– множество рациональных чисел; I
- множество иррациональных чисел; R
– множество действительных чисел; C
– множество комплексных чисел; Ø –
пустое множество (не содержит ни одного
элемента).
Конечные множества состоят из конечного числа элементов.
Бесконечные – из бесконечного числа элементов.
Способы задания множеств:
а) перечислением элементов, например, X={x1, x2,…, xn},
A = {2,4,5,6,8,…};
б)
с помощью характеристического свойства:
A={x|
Р(x)},
где
P(x)
– свойство Р, которым обладает элемент
x,
например,
A={x|
x=![]() };
};
в)
порождающей процедурой, которая описывает
способ получения элементов из уже
имеющихся элементов, например, множество
M={1,2,4,8,16,…}
можно задать так: 1) 1![]() M;
2)m
M;
2)m![]() M
→ 2m
M
→ 2m![]() M.
M.
Определения:
а)
множество В называется подмножеством
множества А (обозначается
![]() ),
если каждый элемент множества В является
элементом множества А:
),
если каждый элемент множества В является
элементом множества А:![]() ,
,![]() -
знак включения;
-
знак включения;
б)
множества А и В называют равными,
если
они состоят из одних и тех же элементов:
![]() и
и![]() ;
;
в)
если
![]() и
и![]() ,
то В является собственным подмножеством
множества А:
,
то В является собственным подмножеством
множества А:![]() -
строгое включение.
-
строгое включение.
Заметим,
что для обозначения отношения включения
применяют как знак строгого, так и не
строгого включения, как для собственных,
так и для несобственных подмножеств. И
только если требуется различить эти
подмножества, различают и эти знаки. Не
следует путать знаки![]() и
и![]() :
: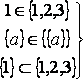 -
верно,
-
верно,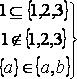 -
не верно.
-
не верно.
Множества
могут быть элементами других множеств.
Множество, элементами которого являются
множества, иногда называют семейством
и обычно обозначают прописными
(готическимими) буквами латинского
алфавита.
Совокупность
всех подмножеств множества А называется
его булеаном или множеством-степенью.
Обозначается
Р(А)
или 2А.
Таким образом, Р(А)
= {B|B![]() A}.
Булеан множества из n
элементов, содержит 2n
элементов.
A}.
Булеан множества из n
элементов, содержит 2n
элементов.
Пример 1.1.1 - A={1,2,3},Р(А) ={Ø,{1},{2},{3},{1,2},{1,3},{2,3}, A}.
Р(А) содержит 8 элементов, 8=23 .
Обычно
в конкретных рассуждениях элементы
всех множеств берутся из одного достаточно
широкого множества U,
которое называется универсальным или
универсумом. Для наглядного изображения
множеств используют диаграммы
Эйлера-Венна, на которых множества
обозначаются точками кругов внутри
прямоугольника, точки которого –
множество U-
универсум (см, рисунок 1.1.1, где A![]() Р(U)).
Р(U)).
|
| |
|
|
|
Рисунок 1.1.1
Операции над множествами.
![]() Р(U)
следующие операции определяются так:
Р(U)
следующие операции определяются так:
а)
объединение (сумма) (обозначается
![]() ,
+): А
,
+): А![]() В
= {x|
x
В
= {x|
x![]() А
или x
А
или x![]() В};
б) пересечение (произведение) (
В};
б) пересечение (произведение) (![]() ,
,![]() ):
А
):
А![]() В
= {x|
x
В
= {x|
x![]() А
и x
А
и x![]() В};
В};
в)
разность ( А \ В; А – В): А \ В = {x|
x![]() А
и x
А
и x![]() В};
В};
г)
симметрическая разность или кольцевая
сумма (![]() ,
,![]() ,
+): А
,
+): А![]() В=
В=
=(А
\ В)![]() (В
\ А) = {x|
(x
(В
\ А) = {x|
(x![]() А
и x
А
и x![]() В)
или (x
В)
или (x![]() В
и x
В
и x![]() А)};
А)};
д)дополнение
множества
А
(![]() ):
):![]() ={x|x
={x|x![]() и x
и x![]() А}=
U
\ A.
Иллюстрация
А}=
U
\ A.
Иллюстрация
операций над множествами диаграммами Эйлера-Венна на рисунке 1.1.2.
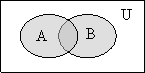
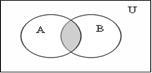
А![]() ВA
ВA![]() B
B
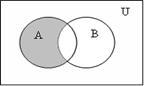
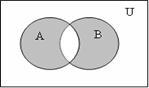
 А
\ В А
А
\ В А![]() В
В
![]()
Рисунок 1.1.2
Операции объединения и пересечения допускают обобщения:
A1![]() A2
A2![]() …
…
![]() An
=
An
=
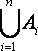 ,A1
,A1![]() A2
A2![]() …
…
![]() An
=
An
=
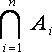 .
.
Свойства операций над множествами
Для
преобразования теоретико-множественных
выражений, упрощения записей, доказательств
теорем и свойств необходимо знать
свойства операций над множествами.
Рассмотрим важнейшие из этих свойств.
Пусть задан универсум U,
тогда
![]() A,
B,
C
A,
B,
C
![]() U
выполняются свойства:
U
выполняются свойства:
Т а б л и ц а 1.1.1
|
1 Идемпотентность
А |
|
2 Коммутативность
А |
|
3 Дистрибутивность
А |
|
4 Ассоциативность
А |
|
5 Свойство поглощения
А |
|
6 Свойства нуля и единицы (констант)
А А |
|
7 Закон де Моргана
|
|
8 Закон двойного отрицания ( двойного дополнения или инволютивности)
|
|
9 Свойство дополнения A |
Доказать
эти свойства можно либо с помощью
диаграмм Эйлера-Венна, либо формальными
рассуждениями, опирающимися на определение
операций, например, докажем
![]() =
=![]()
![]()
![]() .
.
1 Доказательство с помощью диаграмм:
а)
![]() А
А![]() В
В![]()
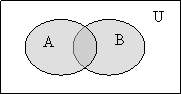
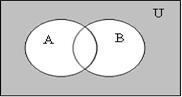
в)
![]()
![]()
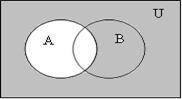
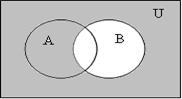
![]()
![]()
![]()
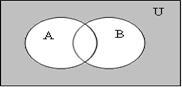
Рисунок 1.1.3
На последних рисунках в пунктах а) и в) отмечена одна и та же область, что доказывает тождество.
2
Докажем
![]() =
=![]()
![]()
![]() формальными рассуждениями.ем
формальными рассуждениями.ем
В
формальных рассуждениях исходят из
того, что А=В
![]() А
А![]() В
и
В
и
В
![]() А,
а последнее имеет место по определению
отношения включения: А
А,
а последнее имеет место по определению
отношения включения: А![]() В
В![]() (x
(x![]() A
A![]() x
x![]() B)
и В
B)
и В![]() А
А![]() (x
(x![]() B
B![]() x
x![]() A),
поэтому:
A),
поэтому:
а)
x![]()
![]()
![]() x
x![]() А
А![]() В
В![]() x
x![]() A
и x
A
и x![]() B
B![]() x
x![]()
![]() и x
и x![]()
![]()
![]() x
x![]()
![]()
![]()
![]() ;
;
б)
x![]()
![]()
![]()
![]()
![]() x
x![]()
![]() и x
и x![]()
![]()
![]() x
x![]() A
и x
A
и x![]() B
B![]() x
x![]() А
А![]() В
В![]() .
.
Теорема. Для любых множеств А и В следующие условия эквивалентны:
а)
А![]() В;
В;
б)
А![]() В=А;
В=А;
в)
А![]() В
=В;
В
=В;
г) А \ В = Ø;
д)
![]()
![]() В
=U.
В
=U.
В примере 1.1.2 свойства операций использованы для упрощения выражения.
Пример
1.1.2 -
![]() .
.
Разбиения и покрытия множеств
Пусть дано множество А. А ={A1, A2, A3, … An}- множество подмножеств А (семейство подмножеств).
Определение. А называется покрытием множества A, если
1.
![]() Ai
Ai
![]() А
(Ai
А
(Ai![]() A,
Ai≠Ø);
2. A=
A,
Ai≠Ø);
2. A=![]() .
.
Определение. А называется разбиением множества А, если
1.
![]() Ai
Ai
![]() А
(Ai
А
(Ai![]() A,
Ai≠Ø);
2. A=
A,
Ai≠Ø);
2. A=![]() ;
3.
;
3.![]() Ai,
Aj
Ai,
Aj![]() А
[Ai
≠ Aj
А
[Ai
≠ Aj
![]() А
i
А
i![]() Аj
= Ø].
Аj
= Ø].
Пример 1.1.3 - А={1,2,3}. А1= {{1,2},{2,3},{1,3}} – покрытие;
А2= {{1},{2},{3}} – разбиение; А3= {{1},{2,3}} – разбиение;
А4= {{1},{3}} – множество подмножеств множества А (ни булеан, ни
покрытие, ни разбиение).
Пример 1.1.4. - N– множество натуральных чисел.
N0 , N1 - множества чётных и нечётных чисел. N ={ N0, N1}- разбиение N.
Прямое произведение множеств
Упорядоченную последовательность из элементов x1,x2,…,xn будем обозначать (x1,x2,…,xn) или <x1,x2,…,xn> и называть кортеж длины n,
упорядоченный набор из n элементов, вектор длины n, n-ка (энка). xi – i-ая координата или компонента. Если n=2, то (x1,x2) – пара, упорядоченная двойка; n=3 - (x1,x2,x3) – тройка, упорядоченная тройка; n=0 - < > - кортеж, не содержащий элементов.
Если
![]() =(x1,…xn),
=(x1,…xn),
![]() =(y1,…yn),
то
=(y1,…yn),
то
![]()
![]() .
Ясно, что (1,2) ≠ (2,1), {1,2}={2,1}.
.
Ясно, что (1,2) ≠ (2,1), {1,2}={2,1}.
Определение.
Прямым (декартовым) произведением
множеств А и В (обозначается А×В)
называется множество таких пар (a,b),
что a![]() A
и b
A
и b![]() В:
В:
А×В
= {(a,b)| a![]() Aи
b
Aи
b![]() В}.
В}.
![]() Обобщение
прямого произведения:
A1×A2×…×An={(a1,a2,…,an)|
a1
Обобщение
прямого произведения:
A1×A2×…×An={(a1,a2,…,an)|
a1![]() A1,
a2
A1,
a2![]() A2
,…, an
A2
,…, an![]() An}.
Если
A=B, то
A×A=A2
;
A×A×…×A=An
; A1=A;
A0={Ø}.
An}.
Если
A=B, то
A×A=A2
;
A×A×…×A=An
; A1=A;
A0={Ø}.
n
Пример 1.1.5 - A={1,2}, B={1,2,3}.
A×B ={(1;1),(1;2),(1;3),(2;1),(2;2),(2;3)};
B×A = {(1;1),(1;2),(2;1),(2;2),(3;1),(3;2)}; A×B ≠ B×A;
A2 = {(1,1),(1,2),(2,1),(2,2)};
Пример
1.1.6 -
R×R = R2
=
{(a,b)|a,b![]() R,
(a,b) –точки
плоскости}.
R,
(a,b) –точки
плоскости}.

