22. Дифференцирование сложных и неявных функции нескольких переменных.

Пусть дана функция двух переменных z = f(u;v) (1) непрерывная, имеющая непрерывные частные производные, а переменные u и v пусть зависят от двух новых независимых переменных х,у (2) которые также непрерывны и имеют непрерывные частные производные. Таким образом, функция z является сложной функцией двух переменных х и у, т.е. (3). Найти производные функцииz по переменным х и у, не пользуясь соотношением (3), а принимая связи (1) и (2). Придадим аргументу х приращение Δ x, тогда функции (2) примут частные приращения ,Так как переменныеu и v получили приращения, то функция z (1) получит полное приращение , равное:Разделим полное приращение наи перейдем к пределу:

По определению частных производных и учитывая, что ибесконечно малые величины более высокого порядка, получим:(4) Аналогично находится частная производная по у:- это есть формулы частных производных от сложной функции. Предположим, что дана сложная функция 4-х переменных

где

Если подставить в функцию z, то она является сложной функцией одного аргумента х, т.е. z = F[x]. Тогда функция z(x) будет иметь полную производную по х. Продифференцируем ее по формуле (4)

или(5)

Получим формулу полной производной.

Дифференцирование неявных функции

1 Функция одного аргумента. Пусть дана некоторая непрерывная функция y = f(x) задана в неявной форме, то есть в виде уравнения F(x;y)=0 (уравнение 1). Требуется найти производную , используя уравнение (1) как функцию двух переменных.Теорема. Если у непрерывная функция от х задана неявно и существуют частные производные 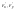,причем, тогда справедлива формула:(Ур 2)

Доказательство. Первый способ. Придавая аргументу х приращение используя определение частной производной и т.д.Второй способ. Представим уравнение (1) как сложную функцию двух переменных z = F(x;y) и y = y(x). Найдем ее полную производную. На самом деле функцияz – тождественный ноль, поэтому ее полная производная равна нулю. . Откуда найдем

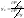или Теорема доказана.

2 Функция многих переменных, заданной неявно. Пусть задана функция трех переменных F(x;y;z) причем х;у – независимые переменные, а функция z зависит от х;у и задана неявно. При дифференцировании по х, переменную у считаем постоянной, поэтому можно предполагать, что z –неявная функция относительно одного аргумента х; F(x,const,z)=0. Следовательно, к этому уравнению можно применить уравнение (2), где вместо у возьмем z, тогдааналогично,(Ур 3)

Обобщим формулу (3). Пусть функция u многих аргументов задана неявно F(x;y;z;..;t;u)=0, тогда частные производные определяются по формуле

Таким образом, частные производные функции нескольких переменных, заданных неявно, равны отношению частных производных по одной переменной к частной производной по переменной функции, взятой с обратным знаком.

23. Экстремум функции двух переменных. Необходимые и достаточные условия экстремума Необходимый признак экстремума: Если в точке дифференцируемая функцияимеет экстремум, то ее частные производные в этой точке равнынулю:

, .Доказательство: Допустим, что функция имеет в точкеэкстремум. Согласно определению экстремума функцияпри постоянном ,как функция одного достигает экстремума при. Как известно, необходимым условием для этого является обращение в нуль производной от функциипри,т. е.

.Аналогично функция при постоянном, как функция одного , достигает экстремума при . Значит, Что и требовалось доказать.Точка, координаты которой обращают в нуль обе частные производные функции , называется стационарной точкой функции. Уравнение касательной плоскости к поверхности :для стационарной точки принимает вид.Следовательно, необходимое условие достижения дифференцируемой функцией экстремума в точкегеометрически выражается в том, что касательная плоскость к поверхности - графику функции в соответствующей ее точке параллельна плоскости независимых переменных.Для отыскания стационарных точек функциинужно приравнять нулю обе ее частные производные, . (*) и решить полученную систему двух уравнений с двумя неизвестными. Достаточные условия экстремума для функции нескольких переменных носят значительно более сложный характер, чем для функции одной переменной. Мы рассмотрим эти условия без доказательства только для функции двух переменных.Пусть точка является стационарной точкой функции, т. е. Вычислим в точке значение вторых частных производных функции и обозначим их для краткости буквами A, B и C:Если, то функция имеет в точке экстремум: при A<0 и C<0 и минимум при A>0 и C>0 (Из условия следует, чтоA и C обязательно имеют одинаковые знаки).Если, то точка не является точкой экстремума.Если, то неясно, является ли точка точкой экстремума и требуется дополнительное исследование.