32. Двойные и тройные интегралы, их свойства.

Двойные интегралы, их свойства

Пусть функция z=f(x;y) определена в ограниченной замкнутой области D плоскости xOy. Разобьем D произвольным образом на n элементарных областей, имеющих площади 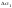,,…,и диаметрыd₁,d₂,…,d_n (наибольшее расстояние между двумя точками границы области называется диаметром области). Выберем в каждой элементарной области произвольную точку P_k(ξ_k,η_k) и умножим значение функции в точке P_k на площадь данной области.

Выражение называетсяинтегральной суммой для функции f(x,y) по области D. Если при max d_k →0 интегральная сумма имеет конечный предел , то этот предел называетсядвойным интегралом от функции f(x,y) в области D и обозначается ⁼ или⁼ . Геометрический смысл двойного интеграла: еслиf(x,y)>0 в области D, то двойной интеграл численно равен объему цилиндрического тела с основанием D, ограниченному сверху поверхностью z=f(x,y). Если функция f(x,y) непрерывна в замкнутой области D, то двойной интеграл существует. Основные свойства двойного интеграла:

1)

2)

3)

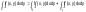
_D=D1+D2.

4) m≤f(x,y)≤M → mS≤≤MS.

Тройные интегралы, их свойства

Пусть функция f(x,y,z) определена в ограниченной замкнутой пространственной области T. Разобьем T произвольным образом на n элементарных областей T₁,T₂,…,T_n с диаметрами d₁, d₂,…,d_n и объемами ∆V1, ∆V2,… ∆Vn В каждой элементарной области возьмем произвольную точку P_k(x_k, y_k, z_k) и умножим значение функции в точке P_k на объем этой области: .

Выражение называется интегральной суммой для функцииf(x;y;z) по области T.

Предел интегральной суммы при стремлении к нулю наибольшего из диаметров элементарных областей называется тройным интегралом от функции f(x;y;z) по области T и обозначается:

Основные свойства тройных интегралов аналогичны свойствам двойных интегралов. Если f(x;y;z) есть функция распределения плотности вещества в области T, то тройной интеграл численно равен массе всего вещества в этой области (физический смысл тройного интеграла).

33. Вычисление двойных и тройных интегралов в прямоугольных координатах.

Вычисление двойных интегралов в прямоугольных координатах

Если функция f(x;y) непрерывна в правильной области D, то двойной интеграл равен двукратному интегралу от этой же функции в области D: .

Сначала вычисляется внутренний интеграл, в котором x считается постоянным.

Вычисление тройных интегралов в прямоугольных координатах

Если функция f(x;y) непрерывна в некотором правильном теле V, то тройной интеграл равен трехкратному интегралу по тому же телу и вычисляется по формуле:

34. Замена переменных в кратных интегралах, переход к полярным, цилиндрическим и сферическим координатам.

В математическом анализекратным или многократным интегралом называют множество интегралов взятых отпеременных. Например:

Замечание: кратный интеграл − это определенный интеграл, при его вычислении всегда получается число.Кратным интегралом (n-кратным) функции f на компактеB называется число I (если оно существует), такое что , такое что(разбиение) си любого выбора точек выполняется:

.