Обучающая последовательность для примера 2.1

x1	x2	d(x)
2 2 0 -2 -2 0 4	1 2 6 8 0 0 -20	1 1 1 -1 -1 -1 -1

8. В чем состоит преимущество гибридных экспертных систем?

14.1 Гибридные интеллектуальные системы

В последние годы интенсивно развиваются гибридные интеллектуальные системы, позволяющие использовать преимущества традиционных средств и методов искусственного интеллекта, и, в то же время, преодолевающие некоторые их недостатки, способные решать задачи, нерешаемые отдельными методами искусственного интеллекта. Гибридные интеллектуальные системы позволяют более эффективно соединять формализуемые и неформализуемые знания за счет интеграции традиционных средств искусственного интеллекта.

За прошедшее время были созданы различные виды систем искусственного интеллекта (или интеллектуальных систем), такие как экспертные системы, нечеткие системы, системы поддержки принятия решений, искусственные нейронные сети, системы планирования движения роботов, генетические алгоритмы.

Интеллектуальные системы (ИС), созданные за последние годы, в зависимости от архитектуры можно классифицировать на однокомпонентные (single component) и многокомпонентные (multi component) ИС .

Однокомпонентные ИС основаны на использовании единственного средства искусственного интеллекта, такого например, как нечеткая логика или искусственная нейронная сеть.

Многокомпонентные ИС объединяют в себе различные средства искусственного интеллекта в единую вычислительную модель. Многокомпонентные ИС представляют собой архитектурно более сложные системы, с компонентами, обладающими собственной функциональностью и объединенными в иерархическую многослойную модель. Корректная работа такой системы, таким образом, зависит от правильной работы всех слоев, ошибка в работе одного из слоев может распространяться на другие слои и отражаться на работе всей системы. Многокомпонентные ИС совмещают различные средства ИИ, которые взаимодействуют между собой для получения решения поставленной задачи

Такое разнообразие интеллектуальных систем определяется необходимостью формализации разнообразных данных и знаний, причем не всегда процесс формализации можно успешно выполнить для данных и знаний любого вида. Вот почему в последние годы стали интенсивно развиваться гибридные интеллектуальные системы (один из видов многокомпонентных интеллектуальных систем) – позволяющие использовать преимущества традиционных средств искусственного интеллекта, и в то же время преодолевающие некоторые их недостатки, способные решать задачи, нерешаемые отдельными методами искусственного интеллекта. Гибридные ИС позволили более эффективно соединять формализуемые и неформализуемые знания за счет интеграции традиционных средств искусственного интеллекта.

Гибридные ИС можно классифицировать, в зависимости от архитектуры, на следующие типы: 1) комбинированные (combination), 2) интегрированные (integration), 3) объединенные (fusion) и 4) ассоциативные (association) гибридные интеллектуальные системы (см. рисунок 2.34).

. Кроме того, можно рассматривать и еще один тип гибридных ИС, появление которого обусловлено стремительным ростом объемов знаний и данных, которые могут храниться в распределенных базах данных, доступных через глобальную сеть Internet. Архитектуру гибридной ИС такого типа можно назвать распределенной (distributed).

Рисунок 2.34. Типы архитектур ГИС

Комбинированные (combination) гибридные интеллектуальные системы

Примером комбинированных гибридных ИС служат гибридные экспертные системы, представляющие собой интеграцию экспертных систем и нейронных сетей и соединяющие как формализуемые знания (в экспертных системах), так и неформализуемые знания (в нейронных сетях).

Примерами комбинированных систем могут служить: гибридная экспертная система для анестезиологии тяжелых пациентов, экспертная система адаптивного обучения, гибридная экспертная система для медицинской диагностики. Нейронная сеть способствует быстрому обучению, в то время как экспертная система позволяет выполнить интерпретацию нечетких данных и объяснить полученное решение. Нейронная сеть может обучаться как с учителем, так и без учителя, может обучаться без переподготовки старой информации

Нечеткая экспертная система – это экспертная система, объединенная с нечеткими множествами. Экспертная система построена на основе знаний, внедренных в обученную нейронную сеть. Экспертная система прозрачна для пользователя, решения, получаемые экспертной системой, легки для понимания, поскольку правила в базе знаний в «if then» формате используют естественный язык.

Внешние входные данные поступают в гибридную систему как через экспертную систему, так и через нейронную сеть. Выходные данные экспертной системы и нейронной сети поступают на вход модуля, находящего и объясняющего решения.

Интегрированные (integration) гибридные интеллектуальные системы

В архитектуре интегрированных гибридных ИС главенствует основной модуль-интегратор, который, в зависимости от поставленной цели и текущих условий нахождения решения, выбирает для функционирования те или иные интеллектуальные модули, входящие в систему, и объединяет отклики задействованных модулей.

Экспертная система является интегрирующим модулем и связана с другими компонентами гибридной системы. Вспомогательные подсистемы, такие как база данных, служат связующими звеньями экспертной системы с полнофункциональными внешними базами данных.

Функционирование экспертной системы основано на использовании алгоритма с применением индукционного дерева (алгоритм позволяет генерировать правила на основе образцов наборов данных), известные и существующие правила предлагаются экспертом. Правила могут использоваться как для прямой, так и для обратной последовательности запросов. Так как структура дерева является почти оптимальной, число запросов, требующихся для получения заключения, является минимальным.

База данных также доступна и нейронной сети. Нейронная сеть используется как инструмент обучения. Нейронная сеть может принимать входные данные и использовать их в качестве образцов для обучения (обучаться с учителем). Выходные данные системы могут быть сохранены в базе данных, отображены, например, в графическом виде.

Объединенные (fusion) гибридные интеллектуальные системы

Характерной особенностью нейронных сетей и генетических алгоритмов является их способность к обучению и адаптации посредством оптимизации. Соединение этих методов с другими методами искусственного интеллекта позволяет увеличить эффективность их способности к обучению. Такую архитектуру гибридной ИС можно отнести к объединенному типу. Примерами объединенных гибридных ИС могут служить: гибридная экспертная система для инвестиционных рекомендаций, гибридная экспертная система для определения неисправностей в энергетических системах.

Ассоциативные (association) гибридные интеллектуальные системы

Архитектура ассоциативных гибридных систем предполагает, что интеллектуальные модули, входящие в состав такой системы, могут работать как автономно, так и в интеграции с другими модулями. В настоящее время, из-за недостаточного развития систем такого типа, системы с ассоциативной архитектурой еще недостаточно надежны и не получили широкого распространения.

Распределенные (distributed) гибридные интеллектуальные системы Следующим уровнем в развитии гибридных систем могут стать распределенные интеллектуальные системы, представляющие мультиагентный подход в области распределенного искусственного интеллекта (см. рисунок 2.35). При этом подходе каждый функциональный интеллектуальный модуль работает автономно и взаимодействует с другими модулями (агентами) путем передачи сообщений через сеть. Существующие в настоящее время интеллектуальные системы, такие как экспертные системы, нейронные сети и т.п. могут быть преобразованы в агенты.

Рис. 2.35. Архитектура распределенной гибридной ИС

В процессе преобразования интеллектуальные модули могут быть дополнены управляющими и коммуникативными знаниями, необходимыми для их объединения в мультиагентную интеллектуальную распределенную систему.

Интеллектуальная обучающая система основана на экспертной системе, направленной на управление процессом обучения. Экспертная система использует формализм гибридного представления знаний, названного нейроправилами. Система состоит из следующих компонентов: 1) домена знаний, 2) модели пользователя, 3) педагогической модели, 4) машины логического вывода и 5) пользовательского интерфейса. Домен знаний содержит знания, относящиеся к изучаемой теме и представляющие актуальный обучающий материал. Домен состоит из двух частей: 1) понятий знаний и 2) курсовых блоков. Курсовые блоки содержат обучающий материал, представляемый пользователям системы как Web-страница. Каждый курсовой блок ассоциируется с определенным числом понятий знаний. Система поддерживает варианты одной и той же страницы (курсового блока) с различными представлениями знаний. Модели пользователя применяются для записи информации, связанной с пользователем. Модели пользователей обновляются в течение всего процесса обучения. Педагогическая модель формирует процесс обучения. Она предлагает инфраструктуру знаний для адаптации презентации изучаемого материала в соответствии с данными, содержащимися в модели пользователя.

Формализм представления знаний в экспертной системе основан на нейроправилах, гибридных правилах, интегрирующих символические правила с нейровычислениями. Нейроправила создаются либо на основе эмпирических данных (обучающих шаблонов), либо на основе символических правил. Каждое нейроправило индивидуально обучается посредством специального алгоритма. Механизм вывода основан на стратегии обратного вывода.

9. Дайте определение декартову произведению.

_Пусть A₁,…, A_n - нечеткие подмножества универсального множества U₁,…,U_n соответственно. Декартово произведение этих подмножеств обозначается _{и определяется как нечеткое подмножество множества с функцией принадлежности}

10. Дайте определение нечеткой переменной.

Нечеткая переменная характеризуется тройкой (X, U, R(X; u)), где X – название переменной), U – универсальное множество (конечное или бесконечное), u – общее название элементов множества U, представляющее собой нечеткое ограничение на значения переменной u, обусловленное X. [Как и в случае обычных (не нечетких) переменных, вместо R(X; u) мы будем писать сокращенно R(X), R(u) или R(x), где x – общее название значений переменной X, и будем называть R(X; u) ограничением на u или ограничением, обусловленным X]. Неограниченная обычная (не нечеткая) переменная u является для X базовой переменной.

Уравнение назначения для X имеет вид

X = u: R(X)

и отражает то, что элементу x назначается значение u с учетом ограничения R(X).

Ту степень, с которой удовлетворяется это равенство, будем называть совместимостью значения u с R(X) и обозначать ее через c(u). По определению

где μ_R(u) – степень принадлежности u ограничению R(X).

11. Дайте определение операции импликации.

В традиционной логике материальная импликация → определяется как логическая связка для пропозициональных переменных. Так, если А и В – пропозициональные переменные, то таблица истинности для А → В, или, что эквивалентно, ЕСЛИ А, ТО В, записывается в таком виде

В обычных рассуждениях, однако, выражение ЕСЛИ А, ТО В употребляется в ситуациях, в которых А и В – нечеткие множества, а не пропозициональные переменные. Например, в случае высказывания ЕСЛИ Джон болен, ТО Джон капризен, которое можно сокращенно записать как болен → капризен, болен и капризен в сущности – названия нечетких множеств.

То же самое справедливо по отношению к высказыванию ЕСЛИ яблоко красное, ТО яблоко спелое, где красное и спелое играют роль нечетких множеств.

Чтобы обобщить понятие материальной импликации на нечеткие множества, предположим, что U и V – два возможно различных универсальных множества, а A, B и C – нечеткие подмножества U, V и V соответственно.

Сначала определим смысл высказывания ЕСЛИ А, ТО В, ИНАЧЕ С и затем определим ЕСЛИ А, ТО В как частный случай высказывания ЕСЛИ А, ТО В, ИНАЧЕ С.

Высказывание ЕСЛИ А, ТО В, ИНАЧЕ С есть бинарное нечеткое отношение в UV, определяемое следующим образом:

ЕСЛИ А, ТО В, ИНАЧЕ С = А В + С. (1.5)

То есть если A, B и C – унарные нечеткие отношения в U, V и V, тогда ЕСЛИ А, ТО В, ИНАЧЕ С – бинарное нечеткое отношение в UV, которое является объединением декартова произведения A и B и декартова произведения отрицания A и C. Далее высказывание ЕСЛИ А, ТО В можно рассматривать как частный случай высказывания ЕСЛИ А, ТО В, ИНАЧЕ С при допущении, что С – полное множество V. Таким образом,

ЕСЛИ А, ТО В = ЕСЛИ А, ТО В, ИНАЧЕ V = AB + V. (1.6)

В сущности это равнозначно интерпретации высказывания ЕСЛИ А, ТО В высказыванием ЕАЛИ А, ТО В, ИНАЧЕ безразлично.

Полезно заметить, что в терминах матриц отношения А, В и С равенство (1.5) можно выразить как сумму попарных произведений, содержащих А и В (и _{и C)} в виде вектор-столбца и вектор-строки соответственно. Так,

_{ЕСЛИ А, ТО В, ИНАЧЕ C = [A] [B] + [] [C]}

_{Пример 1.6. Проиллюстрируем (1.5) и (1.6) следующим примером. Предположим, что}

_{U = V = 1 + 2 + 3,}

_{А = малый = 1/1 + 0.4/2,}

_{В = большой = 0.4/2 + 1/3,}

_{С = не большой = 1/1 + 0.6/2.}

_Тогда

_{ЕСЛИ А, ТО В, ИНАЧЕ C = (1/1 + 0.4/2)(0.4/2 + 1/3) + (0.6/2 + 1/3)}

_{(1/1 + 0.6/2) =}

_{= 0.4/(1,2) + 1/(1,3) + 0.6/(2,1) + 0.6/(2,2) + 0.4/(2,3) + 1/(3,1) + 0.6/(3,2),}

что можно представить в виде матрицы отношения

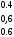
ЕСЛИ А, ТО В, ИНАЧЕ С =. (1.7)

Аналогично

_{ЕСЛИ А, ТО В = (1/1 + 0.4/2) (0.4/2 + 1/3) + (0.6/2 + 1/3)(1/1 + 1/2 + 1/3) = 0.4/(1,2) + 1/(1,3) + 0.6/(2,1) + 0.6/(2,2) + 0.6/(2,3) + 1/(3,1) + 1/(3,2) + 1/(3,3)}

или, эквивалентно,

ЕСЛИ А, ТО В =. (1.8)

12. Для чего необходим этап фаззификации? Стр 41

Однако, ситуация может соответствовать более сложному случаю, когда нечеткими логическими операциями соединены нечеткие высказывания, относящиеся к разным лингвистическим переменным в условии правила нечеткой продукции, т.е. в форме: «β₁ есть α

Пример 1.9. Для иллюстрации выполнения этого этапа рассмотрим пример процесса фаззификации трех нечетких высказываний: “скорость автомобиля малая”, “скорость автомобиля средняя”, “скорость автомобиля высокая” для входной лингвистической переменной — скорость движения автомобиля (см. пример 1.1). Им соответствуют нечеткие высказывания первого вида: “ есть ”, “ есть ”, “ есть ”. Предположим, что текущая скорость автомобиля равна 55 км/ч, т. е. км/ч. (см. рисунок 1.9).

а	б
в

Рис. 1.9. Пример фаззификации входной лингвистической переменной

“скорость автомобиля ” для трех нечетких высказываний

Тогда фаззификация первого нечеткого высказывания дает в результате число 0, которое означает его степень истинности и получается подстановкой значения км/ч в качестве аргумента функции принадлежности терма (рисунок 1.9а). Фаззификация второго нечеткого высказывания дает в результате число 0.67 (приближенное значение), которое означает его степень истинности и получается подстановкой значениякм/ч в качестве аргумента функции принадлежности терма(рисунок 1.9б). Фаззификация третьего нечеткого высказывания дает в результате число 0, которое означает его степень истинности и получается подстановкой значениякм/ч в качестве аргумента функции принадлежности терма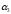(рисунок 1.9в).

13. Из каких основных элементов состоит типичная экспертная система?

14. Какие функции выполняют отдельные блоки экспертной системы? Стр 15

Типичная ЭС состоит из следующих основных компонентов (см. рисунок 1.1): решателя (интерпретатора), рабочей памяти (РП), называемой также базой данных (БД), базы знаний (БЗ), компонентов приобретения знаний, объяснительного и диалогового [I].

База данных предназначена для хранения исходных и промежуточных данных решаемой в текущей момент задачи. Этот термин совпадает по названию, но не по смыслу с термином, используемым в информационно-поисковых системах (ИПС) и системах управления базами данных (СУБД) для обозначения всех данных (и в первую очередь не текущих, а долгосрочных), хранимых в системе.

База знаний в ЭС предназначена для хранения долгосрочных данных, описывающих рассматриваемую область (а не текущих данных), и правил, описывающих целесообразные преобразования данных этой области.

Решатель, используя исходные данные из БД и знания из БЗ, формирует такую последовательность правил, которые, будучи примененными к исходным данным, приводят к решению задачи.

Компонента приобретения знаний автоматизирует процесс наполнения ЭС знаниями, осуществляемый пользователем-экспертом.

Рис.1.1. Схема обобщенной экспертной системы

Объяснительная компонента объясняет, как система получила решение задачи (или почему она не получила решения) и какие знания при этом она использовала, что облегчает эксперту тестирование системы и повышает доверие пользователя к полученному результату.

Диалоговая компонента ориентирована на дружелюбное общение со всеми категориями пользователей, как в ходе решения задач, так и в ходе приобретения знаний, объяснения результатов работы.

В разработке ЭС участвуют представители следующих специальностей: эксперт в той проблемной области, задачи которой будет решать ЭС; инженер по знаниям (когнитолог) — специалист по разработке ЭС; программист — специалист по разработке инструментальных средств (ИтС). Необходимо отметить, что отсутствие среди участников разработки инженера по знаниям (т.е. его замена программистом) либо приводит к неудаче в процессе создания ЭС, либо значительно удлиняет его.

Эксперт определяет знания (данные и правила), характеризующие проблемную область, обеспечивает полноту и правильность введения в ЭС знаний.

Инженер по знаниям помогает эксперту выявить и структурировать знания, необходимые для работы ЭС, осуществляет выбор того ИтС, которое наиболее подходит для данной проблемной области, и определяет способ представления знаний в этом ИтС, выделяет и программирует (традиционными средствами) стандартные функции (типичные для данной проблемной области), которые будут использоваться в правилах, вводимых экспертом.

Уже при разработке первых ЭС стало очевидно, что наиболее ответственным этапом является построение БЗ, для чего в общем случае и необходим посредник — так называемый инженер по знаниям (или аналитик), который должен обеспечить проведение домашинных этапов разработки систем, основанных на знаниях (СОЗ), заключающихся, как правило, в анализе предметной области, извлечении знаний из эксперта и их структурировании.

Эти процедуры оказались самыми тяжелыми, поскольку, с одной стороны, чрезвычайно высок уровень требований, предъявляемых к личности инженера по знаниям (высококвалифицированный специалист в вычислительной науке, обладающий способностями к контакту с экспертами, умеющий побудить эксперта поставлять нужную информацию, умеющий отделять главное от второстепенного и т.д.), а с другой — стали наблюдаться трудности с поисками

собственно экспертов (например, эксперт испытывает затруднения с четкой формулировкой своих знаний, не всегда расположен полностью делиться знаниями и т.п.).

Поэтому почти одновременно с появлением индустрии знаний стали разрабатываться автономные системы, автоматизирующие процессы получения необходимой информации от экспертов. Позднее подобные программные средства получили название «оболочек приобретения», а затем — инструментальных средств.

Программист разрабатывает ИтС, содержащее в пределе все основные компоненты ЭС, осуществляет сопряжение ИтС с той средой, в которой оно может быть использовано.

15. Из каких этапов состоит алгоритм обучения персептрона?

Предлагаемый в настоящий момент алгоритм обучения персептрона состоит из следующих шагов:

6. Присвоить начальным весам персептрона случайные значения.

7. На входы нейрона подать обучающий вектор х = x(t)= [x₀(t), x₁(t), ..., x_n(t)]^T, t = 1,2,….

8. Рассчитать выходное значение персептрона у по формуле (2.3).

9. Сравнить выходное значение у(t) с эталонным значением d=d(x(t)), содержащимся в обучающей последовательности.

10. Модифицировать веса следующим образом:

а) если y(x(t)) ≠ d(x(t), то w_i(t +1) = w_i(t)+d(x(t)) x_i (t);

б) если y(x(t)) = d(x(t)), то w_i(t +1) = w_i (t), т.е. значения весов не изме­няются.

6. Перейти к шагу 2.

Выполнение алгоритма продолжается до тех пор, пока для всех входных векторов, входящих в состав обучающей последовательности, погрешность на выходе не станет меньше априори заданного уровня. На рисунке 2.5 представ­лена блок-схема обучения персептрона. Выполнение одного внутреннего цикла этой схемы соответствует одной так называемой эпохе, которую со­ставляют данные, образующие обучающую последовательность. Выполнение внешнего цикла отражает возможность многократного применения одной и той же обучающей последовательности, пока не будет выполнено условие остановки алгоритма.

Рис. 2.5. Блок-схема алгоритма обучения персептрона

16. Как высказывание 2-го вида можно эквивалентно преобразовать в высказывание 1-го вида?

17. Как высказывание 3-го вида можно преобразовать в высказывание 1-го вида?

18. Какие три вида нечетких лингвистических высказываний Вы знаете? Стр 40

Нечеткие лингвистические высказывания. Нечеткие лингвистические высказывания. Нечеткие лингвистическим высказыванием будем называть высказывание следующих видов.

1. Высказывание «β есть α», где β- наименование лингвистический терм из базового терм- множество Т лингвистической переменной β.

2. Высказывание «β есть α », гдемодификатор, соответствующий таким словам, как: «ОЧЕНЬ», «БОЛЕЕ ИЛИ МЕНЕЕ», «МНОГО БОЛЬШЕ » и другими, которые могут быть получены с использованием специальных процедур для данной лингвистической переменной.

3. Составные выказывания, образованные из высказываний видов 1 и 2 и нечетких логических операций в форме связок: «И», «ИЛИ», «ЕСЛИ – ТО », «НЕ».

Поскольку в системах нечеткого вывода нечеткие лингвистические высказывания занимают центральное место, далее будем их называть просто нечеткими высказываниями.

Пример 1.7. Рассмотрим некоторые примеры нечетких высказываний. Первое из них – «скорость автомобиля высокая» представляет собой нечеткое высказывание первого вида, в рамках которого лингвистической переменной «скорость автомобиля» присваивается значение «высокая». При этом предполагается, что на универсальном множестве Х переменной «скорость автомобиля» определен соответствующего лингвистического терм «высокая» модификатором «ОЧЕНЬ», который изменяет соответствующего лингвистического терма «высокая» на основе использование некоторой расчетной формулы, например для операции концентрации CON(A) нечеткого множества А для терма «высокая».

Переменной «скорость автомобиля» присваивается значение «высокая», а другой лингвистической переменной «расстояние до перекрестка» присваивается значение «близкое». Эти нечеткие высказывания первого вида соединены логической операцией нечеткая конъюнкция (операции нечеткое «И»).

Правила нечетких продукций в системах нечеткого вывода. Рассматриваемые здесь системы нечеткого вывода являются частным случаем продукционных нечетких систем или систем нечетких правил продукции. Основная особенность нечетких правил формулируется в форме нечетких высказываний вида 1-3 относительно значений тех или иных лингвистических переменных.

Простейший вариант правила нечеткой продукции, которой используется в системах нечеткого вывода, может быть записан в форме:

ПРАВИЛО <#>ЕСЛИ «β₁есть α' », ТО «β₂ есть α''». (1.9)

Здесь нечеткое высказывание «β₁ есть α'» представляет собой условие данного правила нечеткой продукции, а нечеткое высказывание «β₂ есть α''» - нечеткое заключение данного правила. При этом считается, что β_1≠ β_{2 .}

Система нечетких правил продукций. Система нечетких правил продукций или продукционная нечеткая система представляет собой некоторое согласование множества отдельных нечетких продукции в форме «ЕСЛИ А, ТО В», где А и В – нечеткие лингвистические высказывание вида 1,2 или 3. Два последних случая нечетких высказывание требуют дополнительного пояснения.

Рассмотрим вариант использования в качестве условия или заключение в некотором правиле нечеткой продукции нечеткого высказывания вида 2, т.е. вида:

«β есть α », (1.10)

гдемодификатор, определяемые процедурамиG и M лингвистической переменной β . Пусть терму α соответствует нечеткому множеству А. В этом случае исходное нечеткое высказывание :«β есть α » можно преобразовать к виду 1 в форме нечеткое высказывание: «β есть α'», где терм α', получается на основе применения определенной процедурамиG и M операции к нечетному множеству А. Полученное в результате подобной операции нечеткое множество А' принимается за значение терм – множества α'.

Если в качестве условия или заключения используется составные нечеткие высказывание, т.е. образованные из высказываний .видов 1 и 2 и нечетких логических операциями в форме связок: «И», «ИЛИ», «ЕСЛИ-ТО», «НЕ», то ситуация несколько усложняется. Поскольку вариант использования нечетких высказываний вида 2 сводится к нечетким высказыванием вида 1, то эта ситуация может соответствовать простейшему случаю, когда нечеткими логическими операциями соединены нечеткие высказывания, относящиеся к одной и той же лингвистической переменной, т.е. в форме:

«β есть α'» ОП «β есть α», (1.11)

где ОП – некоторая из бинарных. операций нечеткой конъюнкции «И» или нечеткой дизъюнкции «ИЛИ».

Примечание. Поскольку нечеткая импликация и нечеткая эквивалентность могут быть выражены через операции нечеткой конъюнкции и нечеткой дизъюнкции, а нечеткое отрицание в данном контексте является по сути модификатором, ограничимся рассмотрением только двух указанных выше нечетких операций.

Очевидно, в этом простейшем случае нечеткое высказывание: «β есть α*» , где терм – множеству α* соответствует нечеткое множество А*, равное пересечению нечетких множеств А' и А'' , которое соответствует термам α' и α''.

Соответственно, нечеткое высказывание: «β есть α'» ИЛИ «β есть α''» эквивалентно нечеткому высказыванию: «β есть α*», где терм – множеству α* соответствует нечеткое множество А*, равное объединению нечетких множеств А' и А''.

Пример 1.8. Рассмотрим составное нечеткое высказывание вида 3: «скорость автомобиля средняя и скорость автомобиля высокая». Ему соответствуют два нечетких высказывания первого вида, соединенные логической операцией нечеткой конъюнкции. Тогда исходное нечеткое высказывание эквивалентно нечеткому высказыванию первого вида: «скорость средняя и высокая».

Рассмотрим аналогичное составное нечеткое высказывание вида 3: «скорость автомобиля средняя или скорость автомобиля высокая». Ему также соответствуют два нечетких высказывания первого вида, соединенные логической операцией нечеткой дизъюнкции. Тогда исходное нечеткое высказывание эквивалентно нечеткому высказыванию первого вида «скорость автомобиля средняя или высокая».

19. Как работает система автоматического регулирования в нечеткой среде?

Примеры использования систем нечеткого вывода в задачах управления стр 60

Одним из основных направлений практического использования систем нечеткого вывода является решение задач управления различными объектами или процессами. В этом случае построение нечеткой модели основывается на формальном представлении характеристик исследуемой системы в терминах лингвистических переменных. Поскольку кроме алгоритма управления, основными понятиями систем управления являются входные и выходные переменные, то именно они рассматриваются как лингвистические переменные при формировании базы правил в системах нечеткого вывода.

В общем случае цель управления заключается в том, чтобы на основе анализа текущего состояния объекта управления определить значения управляющих переменных, реализация которых позволяет обеспечить желаемое поведение или состояние объекта управления. В настоящее время для решения соответствующих задач используются общая теория управления, в рамках которой разработаны различные алгоритмы нахождения оптимальных законов управления объектами различной физической природы.

Не вдаваясь в детальное обсуждение концепций классической теории управления, рассмотрим лишь основные определения, необходимые для понимания особенностей и места систем нечеткого вывода при решении задач управления.

Базовая архитектура или модель классической теории управления основывается на представлении объекта и процесса управления в форме некоторых систем (рисунке 1.19).

Рис. 1.19. Архитектура компонентов процесса

управления с обратной связью

При этом объект управления характеризуется некоторым конечным множеством входных параметров и конечным множеством выходных параметров. На вход системы управления поступают некоторые входные переменные, которые формируются с помощью конечного множества датчиков. На выходе системы управления с использованием некоторого алгоритма управления формируется множество значений выходных переменных, которые еще называют управляющими переменными или переменными процесса управления. Значения этих выходных переменных поступают на вход объекта управления и, комбинируясь со значениями входных параметров объекта управления, изменяют его поведение в желаемом направлении.

Рассмотренная архитектура называется процессом управления с обратной связью, а используемые для управления техническими объектами системы управления - контроллерами.

Наиболее типичными примером рассмотренной модели управления является так называемый интегрально-дифференцирующий контроллер или PID- контроллер (proportional-integral-derivative controller). Алгоритм его управления основан на сравнении выходных параметров объекта управления с некоторыми заданными параметрами и определении величины расхождения между ними или ошибки. После этого рассчитываются величины выходных переменных в форме аддитивной суммы величины этой ошибки, значения интеграла и производной по времени в течение некоторого промежутка времени.

Один из недостатков PID- контроллеров заключается в предположении о линейном характере зависимости входных и выходных переменных процесса управления, что существенно снижает адекватность этой модели при решении отдельных практических задач. Другой недостаток модели связан со сложностью выполнения соответствующих расчетов, что может привести к недопустимым задержкам в реализации управляющих воздействий при оперативном управлении объектами с высокой динамикой изменения выходных параметров.

Архитектура или модель нечеткого управления основана на замене классической системы управления системой нечеткого управления, в качестве которой используются системы нечеткого вывода. В этом случае модель нечеткого управления (рисунок 1.19) строится с учетом необходимости реализации всех этапов нечеткого вывода, а сам процесс вывода реализуется на основе одного из рассмотренных выше алгоритмов нечеткого вывода.

Рис. 1.19. Архитектура компонентов процесса нечеткого управления

20. Какая основная идея заложена в нейрокибернетике? Стр 9

Нейрокибернетка. Основная идея этого направления – «Единственный объект, способный мыслить, - это человеческий мозг». Поэтому любое «мыслящее» устройство должно каким-то образом воспроизводить его структуру.

В 1956-1963 годах велись интенсивные прииски моделей и разработка первых программ на их основе. Представители гуманитарных наук: философы, психологи, лигвисты ни тогда ни сейчас не в состоянии были предложить такие алгоритмы. Тогда кибернетики начали создавать собственные модели: лабиринтного поиска, эвристического программирования, математической логики (метод резолюций, обратный вывод, логик-теоретик и т.д.).

Таким образом, нейрокибернетика ориентирована на программно-аппаратное моделирование структур, подобных структуре мозга. Физиологами установлено, что основой человеческого мозга является большое количество (до 10²¹) связанных между собой и взаимодействующих нервных клеток – нейронов. Поэтому усилия нейрокибернетики были сосредоточены на создании элементов, аналогичных нейронам, и их объединении в функционирующие системы. Эти системы принято называть нейронными сетями.

Первые нейронные сети были созданы Розенблатом и Мак-Калоком в 1956-1965 годах. Это были попытки создать системы, моделирующие человеческий глаз и его взаимодействие с мозгом – перцептрон. Оно умело различать буквы алфавита, но было чувствительно к их написанию, постепенно в 70-80-е годы количество работ по этому направлению ИИ стало снижаться – слишком неутешительны были первые результаты. Однако с совершенствованием компьютерной техники это направление постепенно стало развиваться и сегодня оно одно из самых «модных» из информационных технологий.

В конце 80-х годов в Японии был создан первый нейрокомпьютер, или компьютер VI поколения. Затем появились транспьютеры – параллельные компьютеры с большим количеством процессоров. Транспьютерная технология – это только один из десятка новых подходов к аппаратной реализации нейросетей, которые моделируют иерархическую структуру мозга. Основная область применения нейрокомпьютеров сегодня – эта задача распознавания образов, например идентификация объектов по результатам съемки из космоса.

Можно выделить 3 подхода к созданию нейросетей:

1. Аппаратный – создание специальных компьютеров, нерочипов, плат расширения, наборов микросхем, реализующих все необходимые алгоритмы.

2. Программный – создание программ и инструментариев, рассчитанных на высокопроизводительные компьютеры.

3. Гибридный – комбинация первых двух.

21. Какие два научных направления существуют в искусственном интеллекте? Стр 9

Термин «искусственный интеллект» (artificial intelligence) был предложен в 1956 году на семинаре в Дортмунском колледже. Семинар был посвящен разработке методов решения логических, а не вычислительных задач. В английском языке данное словосочетание не имеет той слегка фантастической окраски, которую оно приобрело в довольно неудачном русском переводе. Слово intelligence «умение рассуждать разумно», а вовсе не «интеллект».

Вскоре после признания ИИ отдельной областью науки произошло разделение его на два направления: «нейрокибернетика» и «кибернетика черного ящика». Эти направления развиваются практически независимо, существенно различаясь как в методологии, так и в технологии. И только в настоящее время стали заметны тенденции к сближению этих частей.

Нейрокибернетка. Основная идея этого направления – «Единственный объект, способный мыслить, - это человеческий мозг». Поэтому любое «мыслящее» устройство должно каким-то образом воспроизводить его структуру.

Кибернетика черного ящика. В основу этого подхода был положен принцип, противоположный нейрокибернетики – «не имеет значения, как устроено «мыслящее» устройство, главное, чтобы на заданные входные воздействия оно реагировало так же, как человеческий мозг». Сторонники этого направления мотивировали свой подход тем, что человек не должен слепо следовать природе в своих научных и технологических поисках. Так, например, очевиден успех колеса, которого не существует в природе, или самолета, не машущего крыльями. К тому же пограничные науки о человеке не смогли внести существенного теоретического вклада, объясняющего хотя бы приблизительно, как протекают интеллектуальные процессы у человека, как устроена память и как человек познает окружающий мир.

Это направление ИИ было ориентировано на поиски алгоритмов решения интеллектуальных задач на существующих моделях компьютеров.

22. Какие три причины вызвали огромный интерес к экспертным системам? Стр 12

Огромный интерес к ЭС со стороны пользователей вызван тремя причинами:

1. Во-первых, они ориентированы на решение широкого круга задач в неформализованных областях, на приложения, которые до недавнего времени считались малодоступными для вычислительной техники.

2. Во-вторых, с помощью ЭС специалисты, не знающие программирования, могу! самостоятельно разрабатывать интересующие их приложения, что позволяет резко расширить сферу использования вычислительной техники.

3. В-третьих, ЭС при решении практических задач достигают результатов, не уступающих, а иногда и превосходящих возможности людей-экспертов, не оснащенных ЭВМ.

23. Каковы особенности экспертных систем? Стр 14

Экспертные системы не отвергают и не заменяют традиционного подхода к программированию, они отличаются от традиционных программ тем, что ориентированы на решение неформализованных задач и обладают следующими особенностями:

1) алгоритм решения не известен заранее, а строится самой ЭС с помощью символических рассуждений, базирующихся на эвристических приемах;

2) ясность полученных решений, т.е. система «осознает» в терминах пользователя, как она получила решение;

3) способность анализа и объяснения своих действий и знаний;

4) способность приобретения новых знаний от пользователя-эксперта, не знающего программирования, и изменения в соответствии с ними своего поведения (открытая система);

5) обеспечение «дружественного», как правило, естественно-языкового (ЕЯ) интерфейса с пользователем.

24. Какой функцией характеризуется нечеткое множество? Стр 24

Нечеткое множество A универсального множества U характеризуется функцией принадлежности μ_A(u): → [0,1], которая ставит в соответствие каждому элементу _число μ_A(u) из интервала [0,1], характеризующее степень принадлежности элемента u подмножеству A.

25. По каким признакам классифицируются экспертные системы? Стр 18

Классификация экспертных систем. Экспертные системы как любой сложный объект можно определить только совокупностью характеристик. Выделим следующие характеристики ЭС: А. Назначение; Б. Проблемная область; В. Глубина анализа проблемной области; Г. Тип используемых методов и знаний; Д. Класс системы; Е. Стадия существования; Ж. Инструментальные средства.

Перечисленный набор характеристик не претендует на полноту в связи с отсутствием общепринятой классификации), а определяет ЭС как целое, не выделяя отдельных компонентов (способ представления знаний, решения задач и т.п.).

А. Назначение определяется следующей совокупностью параметров: цель создания ЭС — для обучения специалистов, для решения задач, для автоматизации рутинных работ, для тиражирования знаний экспертов и т.п.; основной пользователь — не специалист в области экспертизы, специалист, учащийся.

Б. Проблемная область может быть определена совокупностью параметров: предметной областью и задачами, решаемыми в предметной области, каждый из которых может рассматриваться с точки зрения как конечного пользователя, так и разработчика ЭС.

С точки зрения пользователя, предметную область можно характеризовать описанием области в терминах пользователя, включающим наименование области, перечень и взаимоотношение подобластей и т.п., а задачи, решаемые существующими ЭС, — их типом. Обычно выделяют следующие типы задач:

• интерпретация символов или сигналов — составление смыслового описания по входным данным;

• предсказание — определение последствий наблюдаемых ситуаций;

• диагностика — определение состояния неисправностей, заболеваний по симптомам;

• конструирование — разработка объекта с заданными свойствами при соблюдении установленных ограничений;

• планирование — определение последовательности действий, приводящих к желаемому состоянию объекта;

• слежение — наблюдение за изменяющимся состоянием объекта и сравнение его показателей с установленными или желаемыми;

• управление — воздействие на объект для достижения желаемого поведения.

С точки зрения разработчика целесообразно выделять статические и динамические предметные области. Предметная область называется статической, если описывающие ее исходные данные не изменяются во времени (точнее рассматриваются как не изменяющиеся за время решения задачи). Статичность области означает неизменность описывающих ее исходных данных. Если исходные данные, описывающие предметную область, изменяются за время решения задачи, то предметную область называют динамической. Кроме того, предметные области можно характеризовать следующими аспектами: числом и сложностью сущностей, их атрибутов и значений атрибутов; связностью сущностей и их атрибутов; полнотой знаний; точностью знаний (знания точны или правдоподобны; правдоподобность знаний представляется некоторым числом или высказыванием).

Решаемые задачи, с точки зрения разработчика ЭС, также можно разделить на статические и динамические. Будем говорить, что ЭС решает динамическую или статическую задачу, если процесс решения задачи изменяет или не изменяет исходные данные о текущем состоянии предметной области.

В подавляющем большинстве существующих ЭС исходят из предположения статичности предметной области и решают статистические задачи. Будем называть такие ЭС статическими. ЭС, которые имеют дело с динамическими предметными областями и решают статистические или динамические задачи, будем называть динамическими. В последние годы стали появляться первые динамические ЭС. Видимо, решение многих важнейших практических неформализованных задач возможно только с помощью динамических, а не статических ЭС. Следует подчеркнуть, что на традиционных (числовых) последовательных ЭВМ с помощью существующих методов инженерии знаний можно решать только статические задачи, а для решения динамических задач, составляющих большинство реальных приложений, необходимо использовать специализированные символьные ЭВМ. На рисунке 1.3 представлена архитектура статической и динамической ЭС]. Статическая ЭС совпадает с традиционной схемой (см. рисунок 1.1).

Решаемые задачи, кроме того, можно характеризовать следующими аспектами: числом и сложностью правил, используемых в задаче; связностью правил; пространством поиска; количеством активных агентов, изменяющих предметную область; классом решаемых задач.

По степени сложности выделяют простые и сложные правила.

К сложным относят правила, текст знаний которых на естественном языке занимает 1/3 страницы и больше. Правила, текст которых занимает менее 1/3 страницы, относят к простым.

По степени связности правил задачи делятся на связные и малосвязные. К связным относят задачи (подзадачи), которые не удается разбить на независимые задачи. Малосвязные задачи удается разбить на некоторое количество независимых подзадач.

Можно сказать, что степень сложности определяется не просто общим количеством правил данной задачи, а количеством правил в ее наиболее связной независимой подзадаче.

Рис. 1.3. Архитектура статической и динамической ЭС

Пространство поиска может быть определено, по крайней мере, тремя подаспектами: размером, глубиной и шириной. Размер пространства поиска дает обобщенную характеристику сложности задачи. Выделяют малые (до 10! состояний) и большие (свыше 10! состояний) пространства поиска. Глубина пространства поиска характеризуется средним числом последовательно применяемых правил, преобразующих исходные данные в конечный результат, ширина пространства — средним числом правил, пригодных к выполнению в текущем состоянии.

Количество активных агентов существенно влияет на выбор метода решения. Выделяют следующие значения данного аспекта: ни одного агента, один агент, несколько агентов.

Класс решаемых задач характеризует методы, используемые ЭС для решения задачи. Данный аспект в существующих ЭС применяет следующие значения: задачи расширения, доопределения, преобразования. Задачи расширения и доопределения являются статическими, а задачи преобразования — динамическими.

К задачам расширения относятся задачи, в процессе решения которых осуществляется только увеличение информации о предметной области. Они не приводят ни к изменению ранее выведенных данных, ни к выбору другого состояния области. Типичный задачей этого класса являются задачи классификации.

К задачам доопределения относятся задачи с неполной или неточной информацией о реальной предметной области. Цель их решения — выбор из множества альтернативных текущих состояний предметной области того, которое адекватно исходным данным. В случае неточных данных альтернативные текущие состояния возникают как результат ненадежности данных и правил, что приводит к многообразию различных доступных выводов из одних и тех же исходных данных. В случае неполных данных альтернативные состояния являются результатом доопределения области, т.е. результатом предположений о возможных значениях недостающих данных.

К задачам преобразования относятся задачи, которые осуществляют изменения исходной или выведенной ранее информации о предметной области и являются следствием изменений либо реального мира, либо его модели.

Большинство существующих ЭС решают задачи расширения, в которых нет ни изменений предметной области, ни активных агентов, преобразующих предметную область. Подобное ограничение неприемлемо при работе в динамических областях.

В. По степени сложности структуры ЭС делят на поверхностные и глубинные. Поверхностные ЭС представляют знания об области экспертизы в виде правил (условие→ действие). Условие полного правила определяет образец некоторой ситуации, при соблюдении которой правило может быть выполнено. Поиск решения состоит в выполнении тех правил, образцы которых сопоставляются с текущими данными (текущей ситуации в РП). Глубинные ЭС, кроме возможностей поверхностных систем, обладают способностью при

возникновении неизвестной ситуации определять с помощью некоторых общих принципов, справедливых для области экспертизы, какие действия следует выполнять.

Г. По типу используемых методов и знаний ЭС делят на традиционные и гибридные. Традиционные ЭС используют в основном неформализованные методы инженерных знаний и неформализованные знания, полученные от экспертов. Гибридные ЭС используют и методы инженерии знаний, и формализованные методы, а также данные традиционного программирования и математики.

Сейчас говорят о трех поколениях ЭС. К первому поколению следует относить статические поверхностные ЭС, ко второму — статические глубинные ЭС (иногда ко второму поколению относят гибридные ЭС), а к третьему — динамические ЭС (вероятно, они, как правило, будут глубинными и гибридными).

Д. В последнее время выделяются два больших класса ЭС (существенно отличающихся по технологии их проектирования), которые условно можно назвать простыми и сложными ЭС. Простая ЭС может быть охарактеризована следующими основными показателями: поверхностная ЭС; традиционная ЭС (реже гибридная); выполненная на персональной ЭВМ. Сложная ЭС может быть охарактеризована следующими показателями: глубинная ЭС; гибридная ЭС; выполненная либо на символьной ЭВМ, либо на мощной универсальной ЭВМ, либо на интеллектуальной рабочей станции.

Е. По стадиям жизненного цикла ЭС можно подразделить на такие, которые используются при проектировании технических и информационных объектов и применяются интегрированно с САD-system или САПР. На стадии технологического производства ЭС используются совместно с САМ- system как системы технологической подготовки производства, контроля и управления технологическим процессом. На стадии эксплуатации ЭС используются совместно с САЕ- system и обеспечивают интеллектуальную поддержку технического обслуживания сложных систем.

26. Почему метод обучения сети называется методом обратного распространения ошибки?

Алгоритм обратного распространения ошибки

При рассмотрении различных моделей нейронов мы обсуждали основ­ные технологии их обучения. Чаще всего обучение осуществлялось следую­щим образом. Рассчитывалась сумма произведений входных сигналов на со­ответствующие им веса. Далее полученное значение подавалось на вход ис­пользуемой функции активации, на выходе которой появлялся выходной сигнал нейрона. Поскольку требуемое выходное значение нам известно (оно равно эталонному выходному значению, содержащемуся в обучающей выборке), то погрешность сигнала на выходе нейрона определяется доста­точно просто. Искомая погрешность равна разности между фактическим вы­ходным значением и эталонным значением. Аналогичным образом можно рассчитать погрешность для последнего слоя в многослойных сетях. Одна­ко в этой ситуации возникает сложность с расчетом погрешности для скры­тых слоев, поскольку учитель не знает эталонные значения на выходах рас­положенных в них нейронов. На помощь приходит наиболее распростра­ненная технология обучения многослойных нейронных сетей, называемая методом обратного распространения ошибки. Для описания этого ал­горитма необходимо формально определить соответствующую меру по­грешности. Она представляет собой функцию, в которой в роли перемен­ных выступают все веса многослойной нейронной сети. Обозначим иско­мую функцию Q(w), где w - вектор всех весов сети. В процессе обучения будем стремиться минимизировать значение Q (w) относительно вектора w. Разложим функцию Q(w) в ряд Тейлора в непосредственной близости от известного фактического решения w. Разложение в направлении р предста­вим следующим образом:

Q(w+p)=Q(w)+[g(w)]^Tp+0,5p^TH(w)p + ..., (2.95)

где g(w) обозначает вектор градиента, т.е.:

( 2.96)

a H(w) - гессиан, т.е. матрица вторых производных:

(2.97)

Веса модифицируются по формуле

w(t+1) = w(t) + η(t)p(t), (2.98)

где η - коэффициент обучения (способ подбора значения этого параметра бу­дет описан несколько позднее).

Веса могут модифицироваться так долго, пока функция Q не достигнет минимума либо ее значение не станет меньше априори заданного порога. Та­ким образом, задача сводится к поиску вектора направления р, обеспечиваю­щего уменьшение погрешности на выходе сети на очередных шагах алгорит­ма. Это означает, что на следующих итерациях должно выполняться неравен­ство Q(w(t +1))<Q(w(t)). Ограничим ряд Тейлора, аппроксимирующий функ­цию погрешности Q, линейным разложением, т.е.

Q(w + p) = Q(w) + [g(w)]^Tp. (2.99)

Поскольку функция Q(w) зависит от весов, найденных на шаге t, a Q(w+р) - от весов, найденных на шаге (t+1) то для выполнения неравенства Q(w(t+1))<Q(w(t) достаточно подобрать вектор р(t), при котором g(w(t)^Tp(t)<0. Легко заметить, что это условие выполняется при

p(t)=-g(w(t)). (2.100)

При подстановке зависимости (2.100) в формулу (2.98) получаем следую­щее выражение для изменения весов многослойной нейронной сети:

w(t+ l) = w(t) - ηg(w(t)). (2.101)

Зависимость (2.101) известна в литературе под названием «правило на­искорейшего спуска». Для эффективного использования выражения (2.101) с целью вывода алгоритма обратного распространения ошибки необходимо формально описать структуру многослойной нейронной сети и ввести соот­ветствующие обозначения.

Эта структура изображена на рисунке 2.16. В каждом слое расположено N_k элементов, k =1, ..., L, обозначаемых N^k_i , i = 1, ..., N_k. Элементы N^k_i будем называть нейронами, причем каждый из них может иметь сигмоиду на выходе. Обсуждаемая нейронная сеть имеет N₀ входов, на которые подаются сигналы х₁ (t), ...,x_N0 (t), записываемые в векторной форме как

x = [x₁(t),...,x_N0(t)]^T , t = 1,2,.... (2.102)

Рис.2.16. Многослойная нейронная сеть

Выходной сигнал i-го нейрона в k-м слое обозначается у_i^(k)(t), i = 1,..,N_k, k = 1,..., L. На рисунке 2.17 показана детальная структура i-го нейрона в k-м слое.

Рис. 2.17. Структура нейрона

Нейрон N^k_i имеет N_k входов, образующих вектор

(2.103)

причем x_i^(k)(t) = +1 для i = 0 и k = 1, ...,L.

Обратим внимание на факт, что входной сигнал нейрона N^k_i связан с вы­ходным сигналом (k - 1)-го слоя следующим образом:

для

для

для

(2.104)

На рисунке 2.17 символом w_ij^(k) (t) обозначен вес входа i-го нейрона, i=1,…N_k, расположенного в k-м слое, который соединяет этот нейрон с j-м входным сигналом x_i^(k)(t), j=0,1,...,N_k. Вектор весов нейрона N^k_i будем обозначать

, k=1,...,L, i = 1..,,N_k. (2.105)

Выходной сигнал нейрона N^k_i в момент t, t = 1,2,... определяется как

y_i^(k)(t) = f(si^(k)(t)), (2.106)

причем

(2.107)

Отметим, что выходные сигналы нейронов L-го слоя

(2.108)

одновременно являются выходными сигналами сети в целом. Они сравни­ваются с так называемыми эталонными сигналами сети

(2.109)

Погрешность на выходе сети определяется следующим образом:

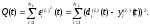(2.110)

При использовании зависимостей (2.101) и (2.110) получаем

(2.111)

Обратим внимание, что

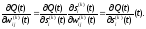(2.112)

Если ввести обозначение

(2.113)

то получим равенство

(2.114)

При этом алгоритм (2.111) принимает вид

(2.115)

Способ расчета значения зависит от номера слоя. Для последнегослоя получаем

(2.116)

Для произвольного слоя k ≠ L получаем

(2.117)

Определим погрешность для i-го нейрона в k-м (не последнем) слое в виде

k = 1,…,L - 1. (2.118)

При подстановке выражения (2.118) в формулу (2.117) получаем

(2.119)

В результате алгоритм обратного распространения ошибки можно запи­сать в виде

(2.120)

(2.123)

(2.124)

Мы рассмотрели последовательность математических выражений, опи­сывающих способ обучения многослойной нейронной сети. Выполнение ал­горитма начинается с подачи обучающей последовательности на вход сети. Вначале эта последовательность обрабатывается нейронами первого слоя. Конечно, под «обработкой» мы понимаем здесь расчет значений выходных сигналов (см. формулы (2.106), (2.107)) для каждого нейрона этого слоя. Полученные сигналы подаются на входы нейронов следующего слоя. Описан­ный цикл повторяется, т.е. вновь рассчитываются выходные сигналы нейро­нов очередного слоя, которые передаются далее - вплоть до выходного слоя. После получения выходного сигнала последнего слоя и выбора соответствую­щего эталонного сигнала из обучающей последовательности рассчитывается погрешность на выходе сети по формуле (2.121). Веса нейронов последнего слоя можно модифицировать при помощи дельта-правила также как и веса оди­ночного нейрона с сигмоидой на выходе - для этого используются формулы (2,121), (2.123), (2,124). Однако этот способ непригоден для модификации ве­сов нейронов в скрытых слоях, поскольку значения для этих нейронов не­известны, а целевая функция, заданная выражением (2.110), зависит от весов всех нейронов сети. Поэтому выходная погрешность распространяется в обрат­ном направлении (от выходного слоя к входному) в соответствии с межслойными соединениями нейронов и с учетом их функций активации (см. формулы (2.122) - (2.124)). Таким образом, название алгоритма объясняется способом его реали­зации, т.е. погрешность «возвращается» от выходного слоя к входному слою.

27. Принцип обучения нейронной сети «без учителя»

Модель нейрона Хебба

Структура модели нейрона Хебба представлена на рисунке 2.12. Она иден­тична структурам моделей типа Адалайн и нейрона с сигмоидой на выходе, однако отличается специфическим методом обучения, называемым правилом Хебба. Это правило существует в двух версиях: «с учителем» и «без учителя». Хебб в работе [1] исследовал функционирование нервных клеток. В процессе своей работы он заметил, что связи между двумя клетками усиливаются, если эти клетки активизируются одновременно.

По аналогии, Хебб предложил ал­горитм, согласно которому веса модифицируются следующим образом:

(2.92)

Причем

(2.93)

Рис. 2.12. Структура нейрона Хебба

При обучении одиночного нейрона мы будем модифицировать значение веса W; пропорционально как значению сигнала, поданного на i-й вход, так и значению выходного сигнала с учетом коэффициента обучения η. Необходи­мо отметить, что при таком подходе мы не используем эталонные выходные значения, следовательно, применяется метод «обучения без учителя». Неболь­шая модификация зависимости (2.93) приводит ко второму методу обучения нейрона Хебба - «обучению с учителем»;

Δw_i = ηx_id, (2.94)

где d - эталонный сигнал.

Некоторым недостатком обсуждаемого алгоритма считается то, что зна­чения весов могут неограниченно увеличиваться. Для устранения этого недо­статка в литературе предлагаются различные модификации правила Хебба.

Пример 2.2

Рассмотрим пример обучения нейрона с применением правила Хебба в версии с учителем. Задача заключается в такой модификации весов нейрона, чтобы он мог различать цифры 1 и 4, схематически изображенные на рисунке 2.13. Если белым полям на этом рисунке сопоставить значение I, а черным полям - значение -1, то получим два вектора, входящих в состав обучающей последовательности:­

[-1 -1 1 -1 -1 1 -1 -1 1 -1 -1 1] – для цифры 1;

[1 -1 1 1 1 1 -1 -1 1 -1 -1 1] – для цифры 4.

Применительно к первому образцу (цифра 1) нам необходимо, чтобы на выходе нейрона появлялся сигнал d = -1, а для второго образца (цифра 4) эта­лонный выходной сигнал должен быть равен d = 1. Поскольку у нас есть вход­ные и выходные эталоны, то веса нейрона на каждой итерации будут модифи­цироваться в соответствии с выражением (2.94). Начальные значения весов равны 0. Нейрон с функцией активации типа «signum» будет обучаться на протяжении 100 эпох, коэффициент обучения выбран равным 0,2. После обу­чения нейрона и подачи на его вход первого обучающего вектора на выходе

Рис. 2.13. Иллюстрация к примеру 2.2

появляется сигнал s = -120, а при подаче на вход второго обучающего вектора на выходе появляется сигнал s = 120. Можно предположить, что с увеличением количества эпох эти значения также будут возрастать. Вектор весов после обучения принял вид: w = [40 00 40 40 000000 0]. Мы видим, что изменениям подверглись только те компоненты вектора весов, которые соот­ветствовали различным значениям конкретных компонент обучающих после­довательностей.

28. Чем отличается обучение отдельного нейрона от обучения нейронной сети?

В предыдущем параграфе было показано, что нейроны могут обучаться, помимо то­ то­го, при описании персептрона мы по­казали, что при наличии п входов он может декомпозировать n-мерное пространство на два подпространст­ва. Эти подпространства разделяют­ся (п-1)-мерной гиперплоскостью. Область задач, которые может решать одиночный персептрон, достаточно узкая. В ка­честве примера можно привести задачу реализации логической фун­кции «исключенное ИЛИ» - XOR. Обучающая последовательность для решения этой задачи представлена в таблице 2.2.

Таблица 2.2

Обучающая последовательность для задачи XOR

x1	x2	d = XOR(x1,x2)
+1 +1 -1 -1	+1 -1 +1 -1	-1 +1 +1 -1

На рисунке 2.14 показаны значения обучающей последовательности из таблице 2.2. Из рисунка следует, что не существует прямой, которая отдели­ла бы точки со значениями функции XOR, равными -1, от точек со зна­чениями, равными 1. В этом случае роль решающей границы играет эл­липс, поэтому алгоритм, изображен­ный на рисунке 2.5,

Рис. 2.14. Иллюстрация к задаче XOR

оказывается не сходящимся. Мы не можем подобрать веса одиночного персептрона так, чтобы он корректно решал задачу XOR. На помощь приходят многослойные сети. Мы вновь обратимся к задаче XOR при обсуждении методов обучения этих сетей. Что представляют собой многослойные сети? Это взаимосвязанные нейроны, размещенные в двух или более слоях. Как правило, используются нейроны с сигмоидой на выходе, однако могут применяться и нейроны с дру­гими функциями активации - например, линейными, которые чаще всего встречаются в последних слоях нейронной сети. Многослойные нейронные сети должны содержать, как минимум, два слоя: входной и выходной. Между ними могут располагаться скрытые слои. Если сеть содержит только два слоя, то входной слой отождествляется со скрытым слоем. В некоторых пуб­ликациях входным слоем называется вектор входных сигналов, подаваемых на нейронную сеть. В рассматриваемых нами структурах сигналами обмени­ваются только нейроны, расположенные в различных слоях.

В пределах одно­го и того же слоя нейроны не могут взаимодействовать друг с другом. Сигна­лы передаются от входного слоя к выходному слою (это объясняет название «однонаправленная сеть»), причем обратные связи с предыдущими слоями отсутствуют. Типовая структура однонаправленной трехслойной сети изоб­ражена на рисунке 2.15.

В следующих разделах мы рассмотрим различные алгоритмы обучения мно­гослойных сетей с учителем. Вначале будет представлен алгоритм обратного распространения ошибки (англ. error backpropagation), а также несколько его модификаций. Следующим будет обсуждаться алгоритм RLS. Далее мы покажем, какое влияние оказывает подбор соответствующей структуры сети на процессы обучения и функционирования нейронной сети. Как отмечалось ранее, представленные в настоящей главе алгоритмы реализуют обучение с учителем, иначе называемое обучением под надзором.

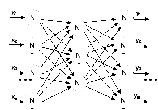
Рис. 2.15. Структура трехслойной нейронной сети

Напомним, что озна­чает этот термин. При использовании обсуждаемых алгоритмов мы предпо­лагаем, что обучающая последовательность состоит из пар, каждая из которых содержит вектор входных значений и вектор эталонных выходных сигналов.

Обучение реализуется следующим образом: вначале входные значения из обучающей последовательности подаются на вход сети, после чего последо­вательно рассчитываются выходные значения каждого нейрона от входного до выходного слоя. Таким способом выясняется реакция сети на сигнал (обра­зец), поступивший на ее вход. Поскольку нам известно, каким должно быть выходное значение (оно содержится в обучающей последовательности), мы будем стараться так модифицировать веса сети, чтобы выходное значение максимально приближалось к эталонному значению. В этом заключается суть алгоритмов рассматриваемого класса, поскольку «учитель» указывает, какой должна быть реакция сети.

29. Чем отличаются экспертные системы от традиционного подхода к программированию? Стр 13

Особенности экспертных систем. Знания, которыми обладает специалист в какой-либо области (дисциплине), можно разделить на формализованные (точные) и неформализованные (неточные). Формализованные знания формируются в книгах и руководствах в виде общих и строгих суждений (законов, формул, моделей, алгоритмов и т.п.), отражающих универсальные знания. Неформализованные знания, как правило, не попадают в книги и руководства в связи с их конкретностью, субъективностью и приблизительностью. Знания этого рода являются результатом обобщения многолетнего опыта работы и интуиции специалистов. Они обычно представляют многообразие эмпирических (эвристических) приемов и правил.

В зависимости от того, какие знания преобладают в той или иной области (дисциплине), ее относят к формализованным (если преобладают точные знания) или к неформализованным (если преобладают неточные знания) описательным областям. Задачи, решаемые на основе точных знаний, называют формализованными, а задачи, решаемые с помощью неточных знаний, - неформализованными. (Речь идет не о неформализуемых, а о неформализованных задачах, т.е. о задачах, которые, возможно, и формализуемы, но эта формализация пока неизвестна).

Традиционное программирование в качестве основы для разработки программы использует алгоритм, т.е. формализованное значение. Поэтому до недавнего времени считалось, что ЭВМ не приспособлены для решения неформализованных задач. Расширение сферы использования ЭВМ показало, что неформализованные задачи составляют очень важный класс задач, вероятно, значительно больший, чем класс формализованных задач. Неумение решать неформализованные задачи сдерживает внедрение ЭВМ в описательные науки. По мнению авторитетов, основной задачей информатики является внедрение ее методов в описательные науки и дисциплины. На основании этого можно утверждать, что исследования в области ЭС занимают значительное место в информатике.

К неформализованным задачам относятся те, которые обладают одной или несколькими из следующих особенностей:

а) алгоритмическое решение задачи неизвестно (хотя, возможно, и существует) или не может быть использовано из-за ограниченности ресурсов ЭВМ (времени, памяти);

б) задача не может быть определена в числовой форме (требуется символьное представление);

в) цели задачи не могут быть выражены в терминах точно определенной целевой функции.

Как правило, неформализованные задачи обладают неполнотой, ошибочностью, неоднозначностью и (или) противоречивостью знаний (как данных, так и используемых правил преобразования).

Экспертные системы не отвергают и не заменяют традиционного подхода к программированию, они отличаются от традиционных программ тем, что ориентированы на решение неформализованных задач и обладают следующими особенностями:

1) алгоритм решения не известен заранее, а строится самой ЭС с помощью символических рассуждений, базирующихся на эвристических приемах;

2) ясность полученных решений, т.е. система «осознает» в терминах пользователя, как она получила решение;

3) способность анализа и объяснения своих действий и знаний;

4) способность приобретения новых знаний от пользователя-эксперта, не знающего программирования, и изменения в соответствии с ними своего поведения (открытая система);

5) обеспечение «дружественного», как правило, естественно-языкового (ЕЯ) интерфейса с пользователем.

Обычно к ЭС относят системы, основанные на знании, т.е. системы, вычислительная возможность которых является следствием их наращиваемой базы знаний и только во вторую очередь определяется используемыми методами. Методы инженерии знаний (методы ЭС) в значительной степени инвариантны тому, в каких областях они могут применяться: военные приложения, медицина, электроника, вычислительная техника, геология, математика, космос, сельское хозяйство, управление, финансы, юриспруденция и т.д. В настоящее время ЭС используются при решении задач следующих типов: принятие решений в условиях неопределенности (неполноты информации), интерпретации символов и сигналов, предсказание, диагностика, конструирование, планирование, управление, контроль и др.

30. Что такое композиционное правило вывода?

Композиционное правило вывода

Основным правилом в традиционной логике является правило modus ponens, согласно которому мы можем судить об истинности высказывания В по истинности высказывания А и импликации А → В. Например, если А – высказывание «Джон в госпитале», то В – высказывание «Джон болен», то если истинно высказывание «Джон в госпитале», то истинно и высказывание «Джон болен» [6].

Во многих привычных рассуждениях правило modus ponens используется не в точной, а в приближенной форме. В отличи от традиционной логики при приближенных рассуждениях главным инструментом будет не правило modus ponens, а так называемое композиционное правило вывода, частным случаем которого является правило modus ponens.

Композиционное правило вывода – это всего лишь обобщение следующей знакомой процедуры. Предположим (см. рисунок 1.6), что имеется кривая y=f(x), а также то, что: x=a, y=f(x), x=a, y=b=f(a). Обобщим теперь этот процесс (см. рисунок 1.7), предположив, что a – интервал, а f(x) – функция, значения которой суть интервал y=b, соответствующий интервалу a, мы сначала построим цилиндрическое множество a’ с основанием a и найдем его пересечение I с кривой, значения которой суть интервалы. Затем спроектируем это пересечение на ось OY и получим желаемое значение y в виде интервала b.

_{Чтобы продвинуться еще на один шаг предположим, что} A – нечеткое множество оси OX, а F – нечеткое отношение в OXOY. Вновь образуя цилиндрическое нечеткое множество A’ и его пересечение с основанием A и его пересечением с нечетким отношением F (см. рисунок 1.8). мы получим нечеткое множество_{, которое является аналогом точки пересечения I на рисунке 1.8.}

_{Рис. 1.6. .Вывод y=b из предпосылок x=a и y=f(x)}

Рис. 1.7. Иллюстрация композиционного правила вывода в случае

переменных со значениями-интервалами

_{Проектируя затем это множество на ось OY. Таким образом, из того, что y=f(x) и x=A – нечеткое подмножество оси OX, мы получим значение y в виде нечеткого подмножества B оси OY. Более конкретно, пусть μA, μA’, μF и μB обозначают функции принадлежности множеств A, A’, F и B соответственно.}

Рис. 1.8. Иллюстрация композиционного правила

_{вывода для нечетких переменных}

_{Тогда по определению множество А}

_{и, следовательно,}

_{Проектируя множество на осьOY, получим}

_{т.е. выражение для функции принадлежности проекции на осьOY. Сравнивая это выражение с определением композиции A и F, видим , что множество B можно представить}

_{B = A ° F,}

_{т.е. операция композиции сводится к максминному произведению матриц.}

Пример 1.5. Предположим A и F имеют вид

А = 0.2/1 + ½ + 0.3/3

и F = 0.8/(1,1) + 0.9/(1,2) + 0.2/(1,3) + 0.6/(2,1) + 1.0/(2,2) + 0.4/(2,3) + 0.5/(3,1) + 0.8/(3,2) + 1.0/(3,3).

Выражая А и F с помощью матриц и образуя матричное произведение, получим

·=

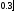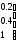Вышеизложенное замечание и примеры помогают обосновать следующее правило вывода.

Пусть U и V – два универсальных множества с базовыми переменными u и v соответственно. Пусть R(u), R(u,v) и R(v) обозначают ограничения на u, (u,v) и v соответственно и представляют собой нечеткие отношения в U, UV и V. Пусть A и F – нечеткие подмножества множеств U и UV. Тогда композиционное правило вывода утверждает, что решение уравнений назначения

R(u) = A,

R(u,v) = F

Имеет вид

_{R(v) = A ° F,}

_{где A ° F – композиция A и F. В этом смысле мы можем делать вывод R(v) = A ° F из того, что R(u) = A и R(u,v) = F.}

_{В качестве простой иллюстрации применения этого правила предположим, что}

_{U = V = 1 + 2 + 3 + 4,}

_{A = малый = 1/1 + 0.6/2 + 0.2/3}

_{F = примерно равны = 1/(1,1) + 1/(2,2) + 1/(3,3) + 1/(4,4) +}

_{+ 0.5/((1,2) + (2,1) + (2,3) + (3,2) + (3,4) + (4,3)).}

_{Другими словами, А - унарное нечеткое отношение в U, называемое малый, F – бинарное нечеткое отношение в UV, называемое примерно равны.}

_{Уравнения назначения в этом случае имеют вид}

R(u) = малый,

R(u,v) = примерно равны,

и, следовательно, R(v) = малый _° примерно равны =

что можно аппроксимировать следующим образом:

R(v) = более или менее малый,

если терм более или менее определяется как оператор увеличения нечеткости, где

K(1) = 1/1 + 0.7/2,

K(2) = 1/4 + 0.7/3,

K(3) = 1/3 + 0.7/4,

K(4) = 1/4.

Заметим, что применение этого оператора к R(u) дает [1 0.7 0.42 0.14] в качестве аппроксимации набора [1 0.6 0.5 0.2].

Итак, используя композиционное правило вывода, из того, что R(u) = малый и R(u,v) = примерно равны, мы вывели, что

R(v) = [1 0.6 0.5 0.2] точно

и R(v) = более или менее малый – в качестве лингвистического приближения. Словами этот приближенный вывод можно записать в виде

u – малый предпосылка

u и v – примерно равны предпосылка

v – более или менее малый приближенный вывод.