5. Угол, образованный двумя пересекающимися плоскостями  и 

(рисунок 95), называется двугранным (плоскости  и   грани этого угла, а линия пересечения этих плоскостей АВ  ребро двугранного угла). Двугранный угол между двумя плоскостями измеряется его линейным углом^о, полученным при пересечении двугранного угла плоскостью , перпендикулярной ребру АВ, а следовательно, и граням плоскости  и :   АВ,   ,    , ^о = L(MN,NF),MN =   ,

NF =   :

При решении данной задачи значительно проще определять не линейный угол ^о, а угол ^о, образованный двумя перпендикулярами СD и СE из произвольной точки пространства С на грани плоскостей  и  заданного двугранного угла.

 

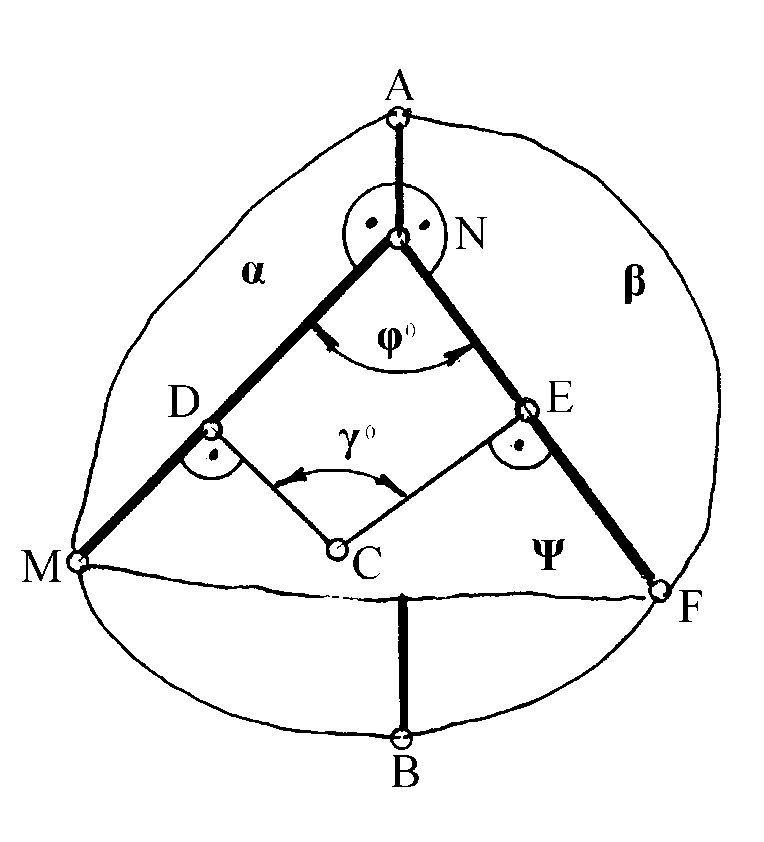
Рисунок 95

 

Прямые СD и СE задают плоскость  , перпендикулярную двум плоскостям  и , и линии их пересечения АВ:

СD  , СD      ,

СE  , СE      ,

  ,     АВ =   .

Между углами ^о и ^о существует зависимость

^о + ^о = 180^о,

так как сумма внутренних углов любого плоского четырехугольника равна 360^о, а два угла четырехугольника С DNE  прямые (С DN = 90^о и

CEN = 90^о).

Таким образом, алгоритм определения линейного угла ^о, измеряющего заданный двугранный угол между плоскостями  и , можно представить в следующем виде:

а) из произвольной точки пространства С опустить перпендикуляры на заданные плоскости  и :

СD  , СE   ;

б) определить полученный угол ^о между этими прямыми:

^о = DCE;

в) вычислить искомый линейный угол ^о как дополняющий угол ^о до 180^о: ^о = 180^о  ^о.

Данной зависимостью ^о = 180^о  ^о можно пользоваться, когда дополнительный угол ^о тупой (^о  90^о). Если же этот угол острый (^о  90^о), то он непосредственно равен искомому линейному углу ^о.

На рисунке 96 в качестве примера показано определение двугранного угла между пересекающимися плоскостями  (АВ  ВС) и  (a  b).

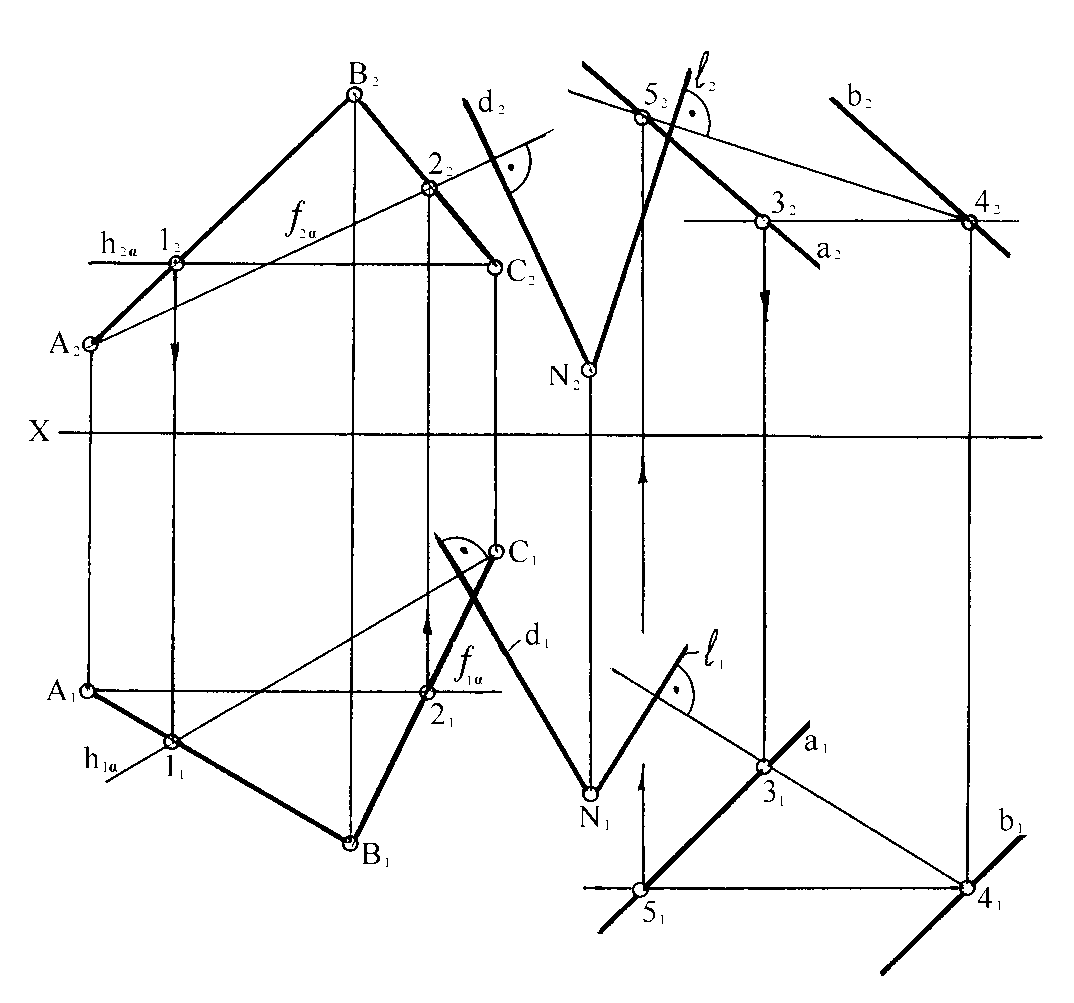
Рисунок 96

 

Двугранный угол между плоскостями измеряется его линейным углом ^о. Из произвольной точки пространства N опустим на заданные плоскости перпендикуляры d и l (d  , l  ):

d₁  h_1, d₂ f _2; l₁  h_1, l₂  f _2.

Плоский угол между этими перпендикулярами будет равен искомому углу ^о либо дополняющему его до 180^о.

Определение натуральной величины этого угла (^о) может быть определено, например, способом вращения вокруг линии уровня (рисунок 89, например, вокруг горизонтали).

Задача на определение двугранного угла несколько облегчается, если задано ребро этого угла АВ (рисунок 97).

 

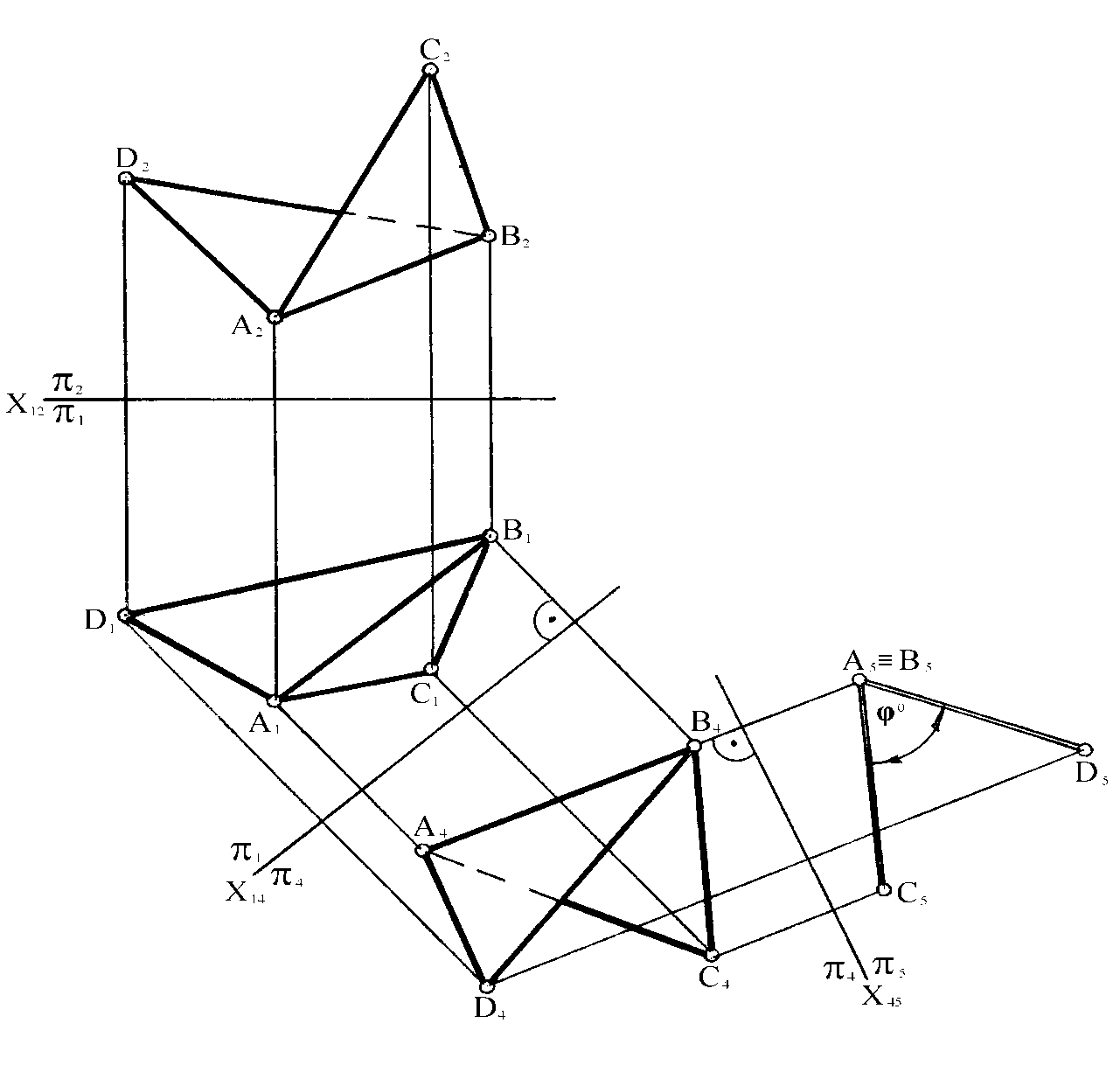
Рисунок 97

 

Для определения линейного угла ^о, измеряющего двугранный угол, достаточно расположить его так, чтобы ребро АВ этого угла оказалось перпендикулярным плоскости проекций. Суть решения задачи состоит в том, что проекцию ребра двугранного угла двойной заменой преобразуют в точку, а проекции граней – в две пересекающиеся прямые. Угол между этими прямыми и будет искомым.

Решение задачи на чертеже выглядит следующим образом (рисунок 97). Сначала выбирается плоскость ₄, параллельная ребру АВ (₄  АВ, Х₁₄  А₁В₁), а затем проводится плоскость ₅, перпендикулярная ребру АВ (₅  АВ, Х₄₅  А₄В₄).

На новую плоскость проекций ₅ ребро АВ спроецируется в виде точки А₅  В₅, грани ABD и ABC – отрезками прямых, а линейный угол ^о – в натуральную величину.