2 Расчетно-графическая работа №2

2.1 Выбор наикратчайшего пути в сети по методу Дейкстры

_{2.1.1 Задание работы:}

- используя исходные данные (см. приложение В) для топологии сети IP, представленной на рисунке 2.1, найдите кратчайшие пути в IP-сети между маршрутизаторами по методу Дейкстры;

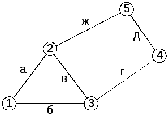
_{Рисунок 2.1 – Исходная топология сети}

- выбор варианта заданий осуществляется по списку журнала преподавателя.

2.2 Ознакомление с сетевыми протоколами

2.2.1 Задание работы:

- используя исходные данные, приведенные в приложении Г нужно кратко описать соответствующий сетевой протокол IP-сети.

2.3 Методические указания к выполнению работы

2.3.1 Алгоритм Дейкстры – это алгоритм на графах, изобретённый нидерландским ученым Э. Дейкстрой в 1959 году. Находит кратчайшее расстояние от одной из вершин графа до всех остальных. Алгоритм широко применяется в программировании и технологиях, например, его используют протоколы маршрутизации OSPF и IS-IS.

При этом в этом алгоритме каждой вершине графа, где установлен маршрутизатор сопоставим метку - минимально известное расстояние от одной вершины до другой. Алгоритм работает пошагово - на каждом шаге он посещает одну вершину и пытается уменьшить метки. Работа алгоритма завершается, когда все вершины посещены.

_{Рассмотрим пример выполнение алгоритма на примере топологии сети передачи данных представленной на рисунке 2.2, состоящей из четырех маршрутизаторов. Между маршрутизаторами имеются каналы. Расстояние между маршрутизаторами обозначено буквами.}

_{Кружками на графе обозначены вершины, линиями - пути между вершинами. В кружках обозначены номера вершин.}

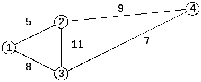
_{Рисунок 2.2 – Граф сети}

_{Метка исходной вершины "а" полагается равной нулю, метки остальных вершин бесконечности. Это означает то, что расстояние от "а" до других вершин пока неизвестны (рисунок 2.3).}

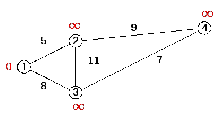
_{Рисунок 2.3 – Нулевой этап}

_{Нулевой этап фиксируется только с целью указать конечный узел с вершиной "1", метка которого равна нулю.}

_{Минимальную метку имеет вершина 1. Ее соседями являются вершины 2 и 3 (рисунок 2.4).}

_{Рисунок 2.4 – Первый шаг}

_{Первый по очереди сосед вершины 1- вершина 2, так как путь до нее минимален (5). При этом длина пути равна сумме кратчайшего расстояния до вершины 1, то есть 0+5=5. Это значение меньше текущей метки вершины 2, бесконечности, поэтому новая метка 2-1 вершины равна 5 (рисунок 2.5).}

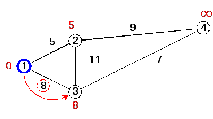
_{Рисунок 2.5 – Новая метка первой вершины}

_{Продолжим аналогичные операции с вершиной 3 (рисунок 2.6)}

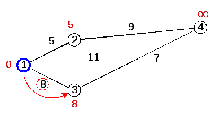
_{Рисунок 2.6 – Новая метка третьей вершины}

_{Все соседи вершины 1 проверены. Вычеркнем ее из графа, чтобы отметить, что эта вершина посещена (рисунок 2.7).}

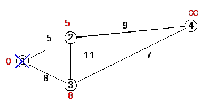
_{Рисунок 2.7 – Новая метка третьей вершины}

_{Снова находим ближайшую из непосещенных вершин. Это вершина 2 с текущим кратчайшим расстоянием до нее равным пяти (рисунок 2.8).}

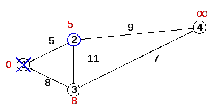
_{Рисунок 2.8 – Посещение вершины 2}

_{Снова пытаемся уменьшить метки соседей выбранной вершины, пытаясь пройти в них через вторую вершину. Соседями вершины 2 являются 3 и 4. Первый по очереди сосед вершины 2- вершина 1, но она уже посещена, поэтому с первой вершиной ничего не делаем. Следующий сосед это вершина 3, так как она имеет минимальную метку из вершин (8), отмеченных как непосещенные. Если идти в нее через вершину 2, то длина такого пути будет равна 16 (5+11). Но текущая метка 3 вершины равна 8<16, поэтому метка не меняется.}

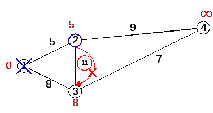
_{Рисунок 2.9 – Посещение вершины 2 (метка не меняется)}

_{Еще один сосед вершины 2 это вершина 4. Путь до нее через вершину 2 составит 14. Так как 14<, устанавливаем метку вершины 4 равной 14 (рисунок 2.10).}

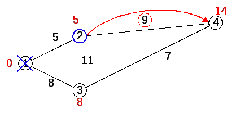
_{Рисунок 2.10 – Посещение вершины 4}

_{Все соседи вершины 2 проверены. Вычеркнем ее из графа, чтобы отметить, что эта вершина посещена (рисунок 2.11).}

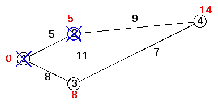
_{Рисунок 2.11 - Отметка вершины 2 как помеченной}

_{Повторяем аналогично выбрав вершину 3 (рисунок 3.12). В результате обработки она будет вычеркнута.}

_{Рисунок 2.12 – Отметка вершины 3 как помеченной}

_{Повторяем для оставшейся вершины 4 (рисунок 2.13).}

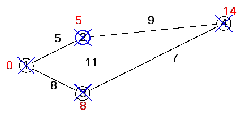
_{Рисунок 2.13 – Отметка вершины 4 как помеченной}

_{Завершение выполнения алгоритма происходит тогда, когда все вершины вычеркнуты. В результате получили кратчайшие пути от вершины 1 до 2 составляет 5, до 3 составляет 8 и 4 составляет 14.}