Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Смоленский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

задания c1 c2

.pdf

Скачиваний:

Добавлен:

01.05.2015

Размер:

519.9 Кб

Скачать

☆

1 / 31 2 3 > Следующая >>>

МАТЕМАТИКА ЕГЭ 2010 Задания С1 и С2

Корянов А.Г.

г.Брянск

Задания С1

● (Д – 2010) Решите систему уравнений

	2	+3x −	x	2	+3x −1 = 7
x		+3x −	x		+3x −1 = 7

		2 sin y = x
2		2 sin y = x

Ответ: x = 2,

y = (−1)n

+πn, n Z.

1. Решите систему уравнений

+ 4 = 5

tgy

−tgy

x −5 + 4 cos y = 0

3π

Ответ: 13;

+ 2π n ,

2. Решите систему уравнений

+ 2sin x = 0

tgx +1 =

cos

5π

Ответ:

+ 2π n; 0,5 , n Z.

3. Решите систему уравнений

−5 2

+ 4 = 0

sin y

x +5cos y +1 = 0

Ответ: (16;π + 2π n), n Z.

4. Решите систему уравнений

−12 cos x +5 = 0

4 cos

− 4 y +16 + 4sin x = 0

−

Ответ:

+ 2π n; 2 , n

5. Решите систему уравнений

+ cos

x − 2 = cos x

y sin

x −sin x −1 = 0

+ 2π n; 2

Ответ:

, n

−

+ 2π k; 2 , k

6. Решите систему уравнений

−

+16

= 0

y −2

cos x =

Ответ: (2π n;3), n Z.

7. Решите систему уравнений

cos x

−10

cos x

+16

= 0

y + 2sin x = 0

−

Ответ:

+ 2π n;3 , n Z.

8. Решите систему уравнений

y+1

= 2 cos x

−y

= 4 cos x +1

+ 2π n; −

Ответ:

1 , n

9. Решите систему уравнений

sin x = y −3

= y −2

cos x

Ответ: (2π n;3), n Z;

−

+ 2π k; 2 , k Z.

10. Решите систему уравнений

sin y = x −6

= x −7

cos y

Ответ: (6;π + 2π n), n Z;

+ 2π k , k Z.

11. Решите систему уравнений

= sin y

−x

= 2sin y +1

−1; (−1)

+π n

Ответ:

, n

12. Решите систему уравнений

sin y

−30 9

sin y

+81

= 0

x + 2 cos y = 0

5π

Ответ:

+ 2π n , n Z.

13. Решите систему уравнений

+3sin y −2 = 0

2sin

− x + 4 cos y = 0

5π

Ответ:

−

+ 2π n , n Z;

5π

+ 2π k ,

k Z.

14. Решите систему уравнений

3sin x = cos 2x +1

+6 y +6 cos x = 0

5π

Ответ:

+ 2π n;3

, n Z;

5π

+ 2π k;

−

k Z;

9 ,

15. Решите систему уравнений

− 4xy + 4 y

−16

= x − 2 y

− 2xy +16

= 0

Ответ: (−4; 4).

16. Решите систему уравнений

2 y

− 2xy

+ x

− 25

= y − x

− 4xy +100 = 0

Ответ: (−10; −5).

17. Решите систему уравнений

2 sin 2 x −7 sin x +3 = 0

6 sin x +5y =13

Ответ: (−1)n π6 +π n; 2 , n Z.

18. Решите систему уравнений

y +11cos y +5 = 0

2 cos

5 cos x − 2 cos y + 4 = 0

2π

Ответ: π + 2π n; ±

+ 2π k , n Z, k Z.

19. Решите систему уравнений

2tgx +5y =12

2tgx +3y = 8

π n; 2

n Z .

Ответ:

20. Решите систему уравнений

3tgx + 4 cos y = 5

3tgx +8cos y = 7

π n; ±

Ответ:

2π k , n Z, k Z.

21. Решите систему уравнений

+ 2 cos x = 0

−3sin x −2 = 0

2sin

5π

Ответ:

−

+ 2π n;

, n Z;

22. Решите систему уравнений

+ 2sin y = 0

y −4 cos y −3 = 0

4 cos

2π

Ответ:

; −

2π n , n Z;

23.Решите систему уравнений

x2 = 8sin y +1

x +1 = 2sin y

Ответ: (−1;π n), n Z;

24.Решите систему уравнений

y2 = 4 cos x +1

y +1 = 2 cos x

Ответ:

+π n; −1 , n

25. Решите систему уравнений

sin x = 0

cos y

x =

y +1

2sin

2 cos

(−1)

+π n;

Ответ:

+π k , n Z, k Z.

26. Решите систему уравнений

cos x = 0

sin y

x +

y = 3

2sin

2 cos

Ответ:

+ 2π n;π k , n Z, k Z;

π n; ±

π k , n Z, k Z.

27. Решите систему уравнений

x − 4 cos x −3 = 0

4 cos

− y −3 + 2sin x = 0

2π

Ответ:

−

2π n;3 , n Z;

−

2π

+ 2π k; −2

28. Решите систему уравнений

cos 2 y = cos y

− 2x = 2sin y

Ответ: (0; 2π n); (2; 2π n);

2π

+ 2π n ;

−1;

+ 2π n

, n Z.

29. Решите систему уравнений

xtgy = 9

x ctgy = 3

Ответ:

+π n , n Z;

−3 3; −

+π k

, k

30. Решите систему уравнений

y tgx = −2

y ctgx = −6

−

Ответ:

+π n; 2 3 , n Z;

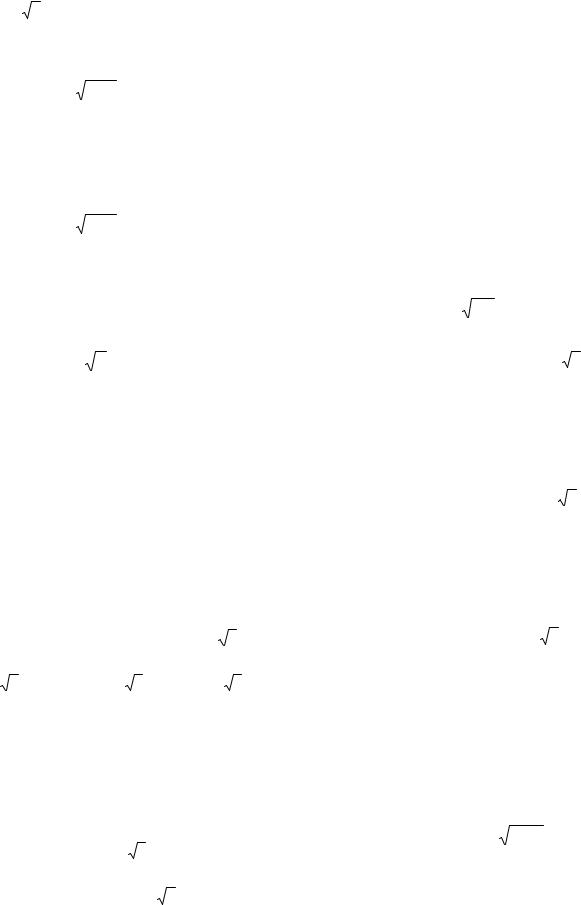
	π
	6	+π k; − 2 3 , k Z.
	6
31. Решите систему уравнений
				sin 2x −cos x			= 0

						y +1
						y +1
					= 4 sin x −3
				y	= 4 sin x −3
Ответ: x =			π	+ 2π n, n Z, y =1.
			2
32. Решите систему уравнений
				sin 2x + cos x				= 0

						y −1
						y −1
					= 4 sin x +3
				y	= 4 sin x +3
Ответ: x =			π	+ 2π n, n Z, y = 7.
			2
33. Решите систему уравнений
				2sin	2	x −3sin x	+1		= 0
					2

						y
						y

			y −cos x = 0

Решение. Из первого уравнения системы следу-

ет	2sin 2 x −3sin x +1 = 0 и		y > 0 .		Пусть
sin x = t , где		−1 ≤ t ≤1.	Из	уравнения
2t 2	−3t +1 = 0	получаем корни	t1	=1,	t2 =	1	,

					2

которые удовлетворяют условию −1 ≤ t ≤1.

а) Если sin x =1, то cos x = 0 и из второго урав-

нения системы имеем

y = 0 .

Это значение не

удовлетворяет условию y > 0 .

б)

Пусть

sin x =

тогда

из тождества

sin 2 x +cos2 x =1

получаем

cos x =

cos x = −

. Отсюда

y =

или y = −

(не

удовлетворяет условию y > 0 ).

Из

уравнения

sin x =

имеем

π + 2π n, n Z.

x =

Таким образом, исходная система имеет реше-

ния x =	π	+ 2π n, n Z, y =			3	.
ния x =	6	+ 2π n, n Z, y =			2	.
	6				2
Ответ: x =			π	+ 2π n, n Z, y =			3	.
Ответ: x =			6	+ 2π n, n Z, y =			2	.
			6				2

Критерии:

Содержание критерия

Баллы

Обоснованно

получен

вер-

ный ответ.

Получен ответ, возможно,

неверный, но только из-за

того, что в решении не уч-

тено, что знаменатель дроби

существует

отличен

от

нуля.

Решение не

соответствует

ни одному из критериев, пе-

речисленных выше.

34. Решите систему уравнений

x +3sin x +1 = 0

2sin

− y

y = −cos x

Ответ: x = −

+ 2π n, n Z, y = −

35. Решите систему уравнений

= 0

−6

sin x

log2 (1 − 2 y)

y = cos x

Ответ: x =

5π

+ 2π n, n Z, y = −

36. Решите систему уравнений

cos x

−12

cos x

+ 27

log7 (1 + 2 y)

= sin x

Ответ: x =

+ 2π n, n Z,

y =

37. Решите систему уравнений

sin x −sin y =1

sin 2 x + cos2

y =1

Ответ:

(−1)

π n; (−1)

k +1

+π k , n Z, k Z.

38. Решите систему уравнений

−5x −3)

cos y = 0

(2x

sin y = x

;

π n

Ответ: (−1)

, n

−

;

−

+ 2π k , k

39. Решите систему уравнений
					1
		cos(x + y) = −
		cos(x + y) = −			2
					2

		sin x +sin y = 3
	π	+ 2π n;	π
Ответ:	3	+ 2π n;	3	+ 2π k ;
	3		3

2π		2π
	+ 2π n;		+ 2π k , n Z, k Z.
	+ 2π n;	3	+ 2π k , n Z, k Z.
3		3
40. Решите систему уравнений
			sin x +sin y =1
						2π
				x − y	=	2π

						3
						3

Решение. Рассмотрим два случая, связанные с раскрытием модуля.

1. Если x − y =

2π

, то y = x −

2π

. Первое урав-

нение системы примет вид

2π

sin x +sin x −

=1;

sin x +sin x cos

2π

−cos x sin

2π

=1;

sin x −

cos x =1;

sin x

−

cos x

=1;

sin x −

=1;

5π

x =

+ 2π n, n Z. Отсюда

y =

π + 2π n, n Z.

2π

2. Если x − y = −

, то y = x +

. Первое

уравнение системы примет вид

2π

sin x +sin x +

=1;

sin x +sin x cos

2π

+cos x sin

2π

=1;

sin x −

sin x +

cos x =1;

sin x

cos x

=1;

sin x +

=1;

x =

π + 2π k, k Z. Отсюда

y =

5π

+ 2π k, k Z.

5π

Ответ:

+ 2π n;

+ 2π n , n

π		5π
	+ 2π k;		+ 2π k , k Z.
6	+ 2π k;	6	+ 2π k , k Z.
6		6

Критерии:

Содержание критерия								Баллы
Обоснованно				получен вер-				2
ный ответ.								2
ный ответ.
Получен ответ, но решение
не верно из-за ошибки в
формулах		или			значениях			1
тригонометрических							функ-	1
тригонометрических							функ-
ций, из-за неверной записи
ответа.
Решение	не			соответствует
ни одному из критериев, пе-								0
речисленных выше.
41. Решите систему уравнений
					sin x = sin 2 y

					cos x = sin y
						≤ x ≤π
					0	≤ x ≤π
					0 ≤ y ≤π

	π	;	π			π
Ответ:	3	;	6	; 0;		2	.
	3		6			2

42. Решите систему уравнений

x + y = 2π3

sin x = 2sin y

π		+π n;	π
Ответ:	2		6	−π n , n Z.

Задания С 2

РАССТОЯНИЯ И УГЛЫ В ПРОСТРАНСТВЕ

Методы решения задач

1.Поэтапно-вычислительный метод

2.Координатный метод

3.Координатно-векторный метод

4.Векторный метод

5.Метод объемов

6.Метод ключевых задач

Ключевые задачи

1. Координаты точки M (x; y; z), делящей отрезок M1M 2 между точками M1 (x1 ; y1 ; z1 ) и

M 2 (x2 ; y2 ; z2 ) в отношении M1M : MM 2 = λ ,

определяются формулами x = x11++λλx2 , y = y11++λλy2 , z = z11++λλz2 .

2.Найти угол между диагоналями смежных граней куба.

3.Найти угол между диагональю куба и скрещивающейся с ней диагональю грани.

4.Найти угол между диагональю куба и плоскостью, проведенной через концы трех ребер куба, выходящих из той же вершины, что и диагональ.

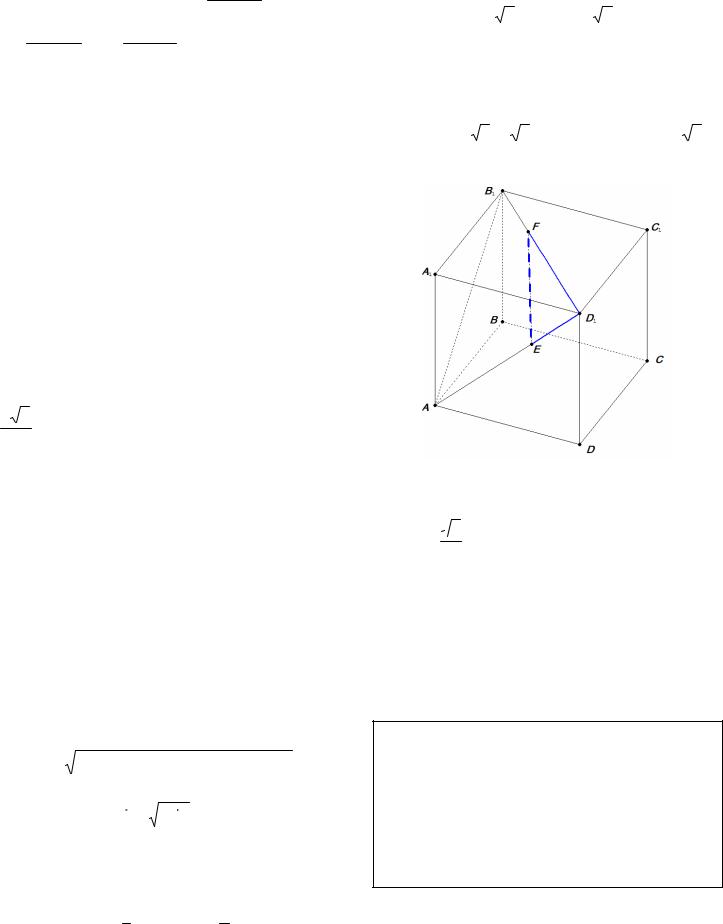
5.В кубе ABCDA1 B1C1 D1 диагональ BD1 пер-

пендикулярна плоскостям AB1C и A1 DC1 и делится ими на три равные части.

6.Отрезки, соединяющие середины противолежащих ребер тетраэдра, пересекаются в одной точке и делятся этой точкой пополам.

7.В правильной треугольной пирамиде скрещивающиеся ребра перпендикулярны.

8.Отрезок, соединяющий середины скрещивающихся ребер правильного тетраэдра, является их общим перпендикуляром и имеет длину

а22 , где а – длина ребра.

9.Любое сечение треугольной пирамиды плоскостью, параллельной ее скрещивающимся ребрам, является параллелограммом.

10.Любое сечение правильной треугольной пирамиды плоскостью, параллельной ее скрещивающимся ребрам, есть прямоугольник.

1. Расстояние между двумя точками

Расстояние между точками А и В можно вычислить:

1)как длину отрезка АВ, если отрезок АВ удается включить в некоторый треугольник в качестве одной из его сторон;

2)по формуле

ρ(A; B)=

− x )2 +(y

− y )2

+ (z

− z )2

, где

A(x1 ; y1 ; z1 ), B(x2 ; y2 ; z2 )

;

3) по формуле

AB2 .

Пример 1. В единичном кубе ABCDA1 B1C1 D1 на диагоналях граней AD1 и D1 B1 взяты точки Е и

F так, что D1 E = 13 AD1 , D1 F = 23 D1 B1 . Найдите длину отрезка EF.

Решение. Длину отрезка EF найдем по теореме косинусов из треугольника D1 EF (рис. 1), в ко-

тором				D F =		2		2 ,		D E =				1	2 , FD E = π
тором				D F =				2 ,		D E =					2 , FD E = π
				1	3						1			3		1	3
					3									3			3
(треугольник AB1 D1									является равносторонним).
Имеем											−2D E D F cos π
	EF 2			= D E 2			+ D F 2				−2D E D F cos π						=
				1				1					1		1	3
																3
=	2	+	8	−2	2			2	2		1	=	2	, откуда EF =				6	.
=		+	9	−2	3			3			2	=	3	, откуда EF =			3		.
9			9		3			3			2		3				3

Рис. 1

Ответ: 36 .

1. (П) Ребра правильной четырехугольной призмы равны 1, 4 и 4. Найдите расстояние от вершины до центра основания призмы, не содержащего эту вершину.

Ответ: 3.

2. Расстояние от точки до прямой

Расстояние от точки до прямой, не содержа-

щей эту точку, есть длина отрезка перпендикуляра, проведенного из этой точки на прямую.

Расстояние между двумя параллельными пря-

мыми равно длине отрезка их общего перпендикуляра.

Расстояние между двумя параллельными пря-

мыми равно расстоянию от любой точки одной из этих прямых до другой прямой.

Расстояние от точки до прямой можно вычислить:

1)как длину отрезка перпендикуляра, если удается включить этот отрезок в некоторый треугольник в качестве одной из высот;

2)используя векторный метод;

3)используя координатно-векторный метод.

Пример 2. При условиях примера 1 найдите расстояние от точки D1 до прямой EF. Решение. Пусть h – длина высоты треугольника D1 EF , опущенной из точки D1 . Найдем h, используя метод площадей. Площадь треугольни-

ка D EF равна										1	D F D E sin FD E =
ка D EF равна											D F D E sin FD E =
				1					2			1	1				1
									2
=			1		2	2	2		3			=	3	.	С		другой				стороны
=		2					3		2			=	9	.	С		другой				стороны
		2		3			3		2				9						D1 EF				равна
площадь								треугольника											D1 EF				равна
	1	FE h				=	6	h	. Из уравнения									3		=	6	h	нахо-
2		FE h				=	6	h	. Из уравнения								9			=	6	h	нахо-
2							6										9				6
дим искомое расстояние															h =		2		.
дим искомое расстояние															h =				.
																3

Замечание. Можно заметить, что выполняется

равенство			FE	2 + D E 2	= D F 2 , то есть тре-
				1	1
угольник D1 EF прямоугольный и длина отрезка
D1 E является искомым расстоянием.
Ответ:		2	.
Ответ:	3		.
	3

1. (П) В единичном кубе ABCDA1 B1C1 D1 найдите расстояние от точки А до прямой:

a) B1 D1 ; б) А1С; в) BD1 .

Ответ: а) 26 ; б) 36 ; в) 36 .

2. (П) В правильной треугольной призме ABCA1 B1C1 , все ребра которой равны 1, найдите

расстояние от точки А до прямой ВС1 .

Ответ: 144 .

3. (П) В правильной шестиугольной призме ABCDEFA1 B1C1 D1 E1 F1 , все ребра которой равны 1, найдите расстояние от точки А до прямой:

а) DЕ; б) D1 E1 ; в) B1C1 ; г) BE1 ; д) BC1 ; е) CE1 ; ж) CF1 ; з) CB1 .

Ответ: а)	3 ; б) 2; в)			7		; г)	2 5	; д)	14	;
Ответ: а)	3 ; б) 2; в)			2		; г)	5	; д)	4	;
				2			5		4
е) 2 ; ж)	30	; з)	30		.
е) 2 ; ж)	5	; з)			.
	5		4

4. (П) Основание прямой призмы

ABCDA1 B1C1 D1	− ромб ABCD,	в котором
АВ =10, АС = 6	7. Боковое ребро	АА1 равно

3 21. Найдите расстояние от вершины В до прямой АС1.

Ответ: 8.

3.Расстояние от точки до плоскости

•Расстояние от точки до плоскости, не со-

держащей эту точку, есть длина отрезка перпендикуляра, опущенного из этой точки на плоскость.

•Расстояние между прямой и параллельной ей плоскостью равно длине их общего перпендикуляра.

•Расстояние между прямой и параллельной ей плоскостью равно расстоянию от любой точки этой прямой до плоскости.

•Расстояние между двумя параллельными плоскостями равно длине их общего перпендикуляра.

•Расстояние между двумя параллельными плоскостями равно расстоянию между точкой одной из этих плоскостей и другой плоскостью.

Расстояние от точки М до плоскости α

1)равно расстоянию до плоскости α от произвольной точки Р, лежащей на прямой l, которая проходит через точку М и параллельна плоскости α ;

2)равно расстоянию до плоскости α от произвольной точки Р, лежащей на плоскости β , ко-

торая проходит через точку М и параллельна плоскости α ;

3) вычисляется по формуле ρ = ρ			r	, где
3) вычисляется по формуле ρ = ρ		1 r		, где
		1 r
ρ = ρ(M ;α),	ρ1 = ρ(M1 ;α),		1
ρ = ρ(M ;α),	ρ1 = ρ(M1 ;α),		OM = r,
OM1 = r1 , MM1 ∩α = O ; в частности,				ρ = ρ1 ,
если r = r1 :

прямая m, проходящая через точку М, пересекает плоскость α в точке О, а точка М1 лежит

на прямой m;

4) вычисляется по формуле

ρ(M ;α)= ρ(M ; ABC)= 3VABCM , где треугольник

S ABC

АВС расположен на плоскости α, а объем пирамиды АВСМ равен VABCM ;

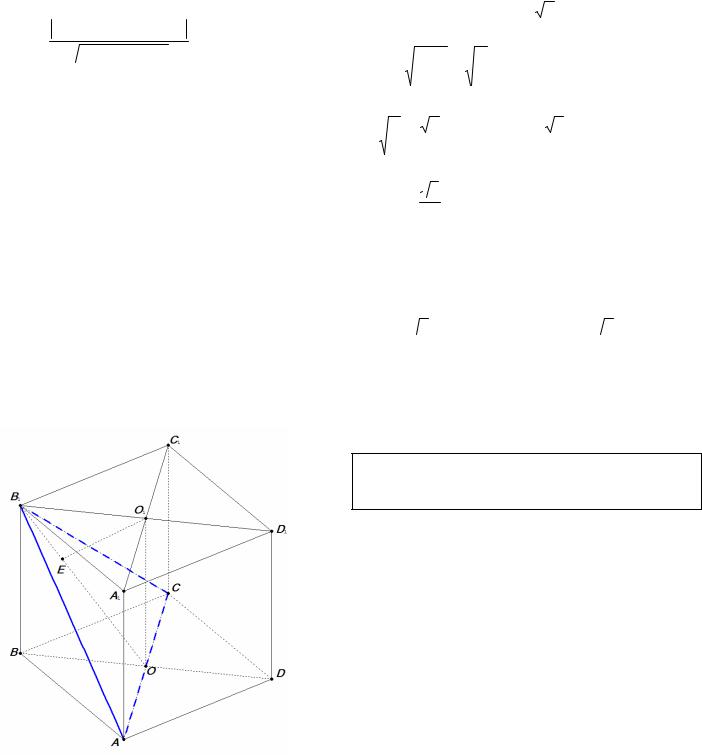
5) вычисляется по формуле

ρ(M ;α)= Ax0 + By0 +Cz0 + D , где

A2 + B2 +C 2

M (x0 ; y0 ; z0 ), плоскость α задана уравнением

Ax + By +Cz + D = 0 ;

6)находится с помощью векторного метода;

7)находится с помощью координатновекторного метода.

Пример 3. В единичном кубе ABCDA1 B1C1 D1 найдите расстояние от точки С1 до плоскости

АВ1С .

Решение. Так как прямая А1С1 параллельна АС, то прямая А1С1 параллельна плоскости АВ1С (рис. 2). Поэтому искомое расстояние h равно расстоянию от произвольной точки прямой А1С1 до плоскости АВ1С . Например, расстояние от центра О1 квадрата A1 B1C1 D1 до плоскости АВ1С равно h.

Рис. 2

Пусть Е – основание перпендикуляра, опущенного из точки О1 на прямую В1О, где О –

центр квадрата ABCD . Прямая О1 Е лежит в плоскости BB1 D1 D , а прямая АС перпендикулярна этой плоскости. Поэтому О1 Е АС и О1 Е - перпендикуляр к плоскости АВ1С , а

О1 Е = h .

Так				как		В О =			2		,		О О =1,	то
Так				как		В О =					,		О О =1,	то
						1		1	2			1
									2
ОВ =			1	+1 =		3	.	Выражая двумя способами
ОВ =				+1 =			.	Выражая двумя способами
	1		2			2
			2			2						В1О1О, получим
площадь					треугольника							В1О1О, получим
h		3	=	2	1 , откуда h =					3			.
h	2		=	2	1 , откуда h =								.
	2			2					3

Ответ: 33 .

1. Ребро AD пирамиды DABC перпендикулярно плоскости основания АВС. Найдите расстояние от вершины А до плоскости, проходящей через середины ребер АВ, АС и AD, если

AD = 2 5, AB = AC =10, BC = 4 5.

Ответ: 2.

4. Расстояние между скрещивающимися прямыми

Расстояние между двумя скрещивающимися прямыми равно длине отрезка их общего перпендикуляра.

Расстояние между скрещивающимися прямыми

1)равно расстоянию от любой точки одной из этих прямых до плоскости, проходящей через вторую прямую параллельно первой прямой;

2)равно расстоянию между двумя параллельными плоскостями, содержащими эти прямые;

3)равно ρ(a;b)= ρ(A;b1 ), где A = aα , b1 = bα : если ортогональная проекция на плоскость α переводит прямую а в точку А, а прямую b в

прямую b1 , то расстояние между скрещивающимися прямыми а и b равно расстоянию от


точки А до прямой b1 ;
4)	вычисляется		по	формуле
ρ(AB;CD)=		6VABCD	где А	и В – точки
ρ(AB;CD)=		AB CD sin ϕ	где А	и В – точки

на одной прямой, С и D – точки на другой прямой, ϕ - угол между данными прямыми;

5)определяется с помощью векторного метода;

6)определяется с помощью координатновекторного метода.

Пример 4. В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1, найдите расстояние между прямыми BD и SA.

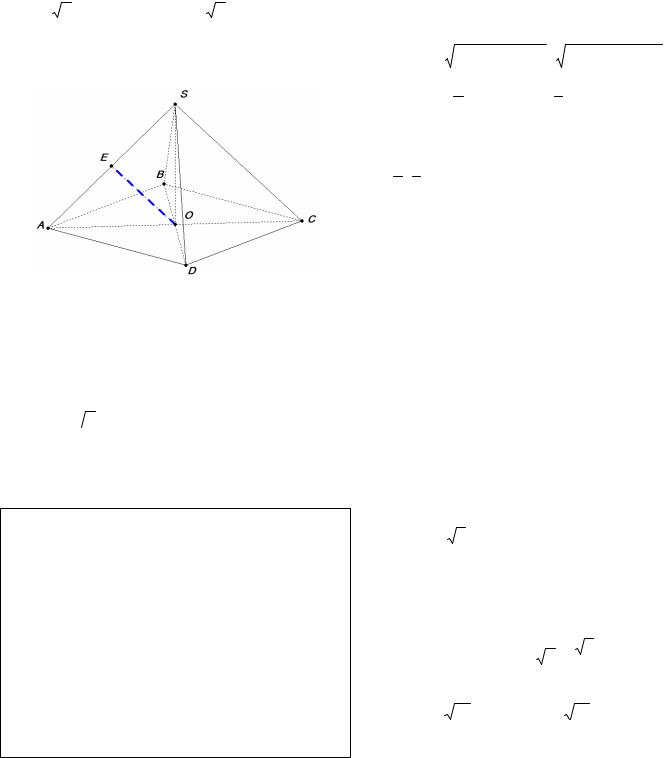
Решение. Пусть Е – основание перпендикуляра (рис. 3), опущенного из точки О на ребро SA. Так как прямая BD перпендикулярна плоскости

AOS, то BD OE .

Таким образом, ОЕ – общий перпендикуляр к скрещивающимся прямым BD и SA.

Найдем его длину, вычислив двумя способа-

ми площадь треугольника AOS.
Из			равенства	AO SO = AS OE, где
AO =	2		, AS =1,	SO =	2	следует, что
AO =	2		, AS =1,	SO =	2	следует, что
	2				2
OE =	1	.
OE =	2	.
	2

Рис. 3

Ответ: 0,5.

1. В пирамиде DABC известны длины ребер:

AB = AC = DB = DC =10, BC = DA =12. Най-

дите расстояние между прямыми DA и ВС.

Ответ: 2 7.

5.Угол между двумя прямыми

•Углом между двумя пересекающимися пря-

мыми называется наименьший из углов, образованных при пересечении прямых.

•0D < (a;b)≤ 90D .

•Углом между скрещивающимися прямыми

называется угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся.

•Две прямые называются перпендикулярными, если угол между ними равен 90D .

•Угол между параллельными прямыми счита-

ется равным нулю.

•При нахождении угла между прямыми используют:

1) формулу cosϕ =	b2	+c2 −a2	для нахожде-

		2bc
		2bc
ния угла ϕ между прямыми m и			l , если сторо-

ны а и b треугольника АВС соответственно параллельны этим прямым;

2) формулу

cosϕ =

или в координатной

форме

x1 x2 + y1 y2

+ z1 z2

cosϕ =

для на-

+ y2 + z2 x2

+ y 2

+ z2

хождения угла ϕ между прямыми m и l , если

векторы p(x1 ; y1 ; z1 ) и q(x2 ; y2 ; z2 ) параллельны соответственно этим прямым; в частности, для того чтобы прямые m и l были перпендикулярны, необходимо и достаточно, чтобы

p q = 0 или x1 x2 + y1 y2 + z1 z2 = 0 ; 3) ключевые задачи.

Пример 5. В кубе ABCDA1 B1C1 D1 найдите угол между прямыми A1 D и D1 E , где Е – середина ребра CC1 .

Решение. Пусть F – середина ребра ВВ1 , а – ребро куба, ϕ - искомый угол.

Так как A1 F D1 E , то ϕ - угол при вершине

A1 в треугольнике A1 FD .

Из треугольника BFD имеем

FD	2		= BD			2		+ BF			2	= 2a			2	+		a2				=		9a2		, а из тре-
FD			= BD					+ BF				= 2a				+			4			=			4	, а из тре-
																			4						4
угольника A1 B1 F получаем
A F		2	= A B					2		+ B F			2	= a		2	+			a2			=		5a	2	, откуда
A F			= A B							+ B F				= a			+						=				, откуда
1					1	1					1								4						4
																			4						4
A F =				a	5		.
A F =							.
1			2
			2
Далее в треугольнике A1 FD используем теоре-
му косинусов
FD	2 = A D2								+ A F 2				−2A D A F cosϕ ,
			1							1						1			1
9a2		= 2a			2	+			5a2		− 2a			2			a 5					cosϕ , откуда
4		= 2a				+				4	− 2a			2				2				cosϕ , откуда
4										4								2
cosϕ =					1				и ϕ = arccos									1			.
cosϕ =					10				и ϕ = arccos									10			.
					10													10

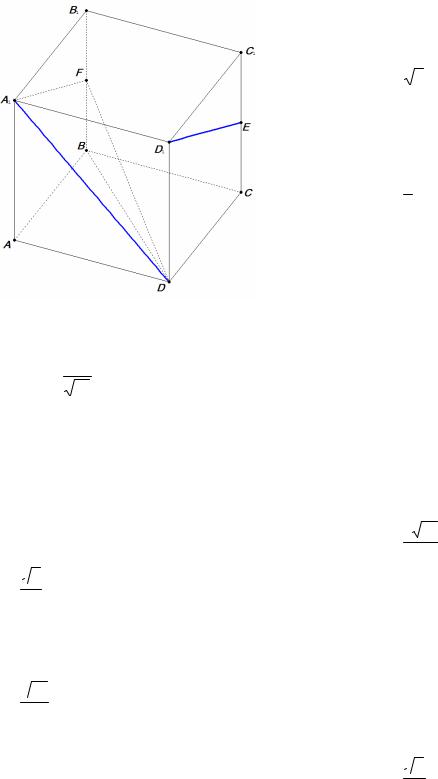
Рис. 4

Ответ: arccos 110 .

1. В кубе ABCDA1 B1C1 D1 точки Е, F – середины ребер соответственно A1 В1 и B1C1 . Найдите ко-

синус угла между прямыми АЕ и BF.

Ответ: 0,8.

2. В кубе ABCDA1 B1C1 D1 точки Е, F – середины ребер соответственно A1 В1 и C1 D1 . Найдите косинус угла между прямыми АЕ и BF.

Ответ: 55 .

3. В кубе ABCDA1 B1C1 D1 точка Е – середина ребра A1 В1 . Найдите косинус угла между прямыми АЕ и ВD1 .

Ответ: 515 .

4.К диагонали куба провели перпендикуляры из остальных вершин куба. На сколько частей и в каком отношении основания этих перпендикуляров разделили диагональ?

Ответ: на три части в отношении 1:1:1.

5.К диагонали A1C куба ABCDA1 B1C1 D1 про-

вели перпендикуляры из середин ребер АВ и AD. Найдите угол между этими перпендикулярами.

Ответ: 60D .

6. К диагонали A1C куба ABCDA1 B1C1 D1 про-

вели перпендикуляры из вершин А и В. Найдите угол между этими перпендикулярами.

Ответ: 60D .

7. В правильной треугольной призме ABCA1 B1C1 , все ребра которой равны 1, найдите

косинус угла между прямыми АВ и A1C .

Ответ:	2	.
	4
8. В
	правильной треугольной		призме
ABCA1 B1C1 , все ребра которой равны 1, найдите
косинус угла между прямыми AВ1 и			BC1 .

Ответ: 14 .

9. Непересекающиеся диагонали двух смежных боковых граней прямоугольного параллелепипеда образуют с плоскостью его основания углы ϕ и ψ. Найдите угол между этими диагоналями.

Ответ: arccos(sin ϕ sinψ )

10. В правильной треугольной	призме
ABCA1 B1C1 , все ребра которой равны 1, точки D,
Е – середины ребер соответственно A1 В1	и B1C1 .

Найдите косинус угла между прямыми АD и

ВЕ. Ответ: 0,7.

11. В правильной треугольной призме ABCA1 B1C1 , все ребра которой равны 1, точка D

– середина ребра A1 В1 . Найдите косинус угла между прямыми АD и BC1 .

Ответ: 32010 .

12. В правильной шестиугольной призме ABCDEFA1 B1C1 D1 E1 F1 , все ребра которой равны

1, найдите косинус угла между прямыми AB1 и

BC1 .

Ответ: 0,75.

13. В правильной шестиугольной призме ABCDEFA1 B1C1 D1 E1 F1 , все ребра которой равны

1, найдите косинус угла между прямыми AB1 и

BD1 .

Ответ: 42 .

14. В правильной шестиугольной призме ABCDEFA1 B1C1 D1 E1 F1 , все ребра которой равны

1, найдите косинус угла между прямыми AB1 и

BE1 .

Ответ: 90D .

15. В правильной шестиугольной призме ABCDEFA1 B1C1 D1 E1 F1 , все ребра которой равны 1, точки G, H – середины ребер соответственно A1 В1 и B1C1 . Найдите косинус угла между прямыми АG и BH.

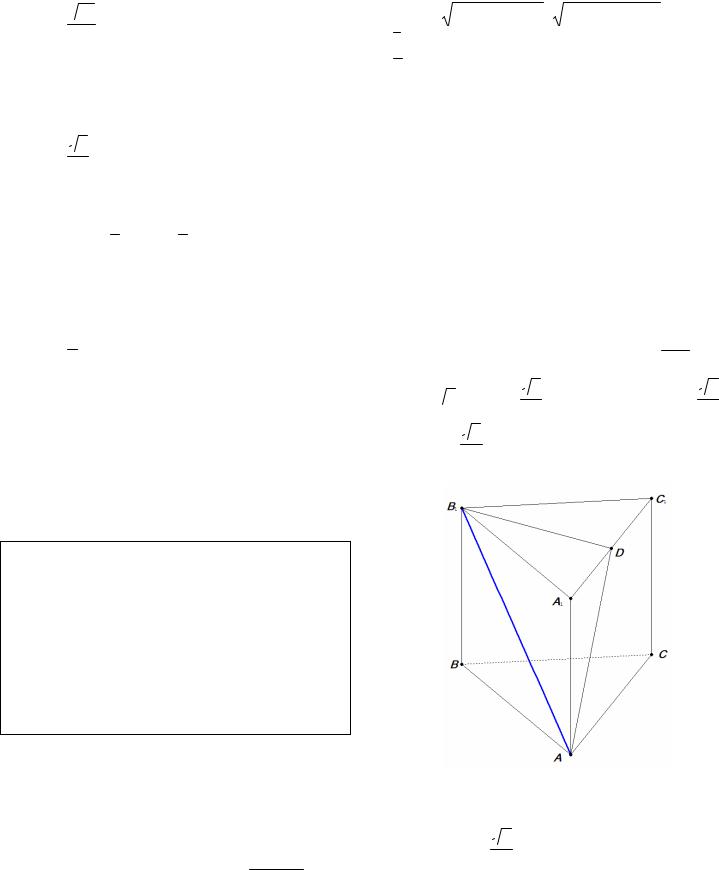
Ответ: 0,9.

16. В правильной шестиугольной призме ABCDEFA1 B1C1 D1 E1 F1 , все ребра которой равны

1, точка G – середина ребра A1 В1 . Найдите косинус угла между прямыми АG и BC1 .

Ответ: 104 .

17. В правильной шестиугольной призме ABCDEFA1 B1C1 D1 E1 F1 , все ребра которой равны

1, точка G – середина ребра A1 В1 . Найдите косинус угла между прямыми АG и BD1 .

Ответ: 55 .

18. Найдите угол между непересекающимися медианами граней правильного тетраэдра.

Ответ: arccos 16 ; arccos 23 .

19. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки Е, F – середины ребер соответственно SB и SC. Найдите косинус угла между прямыми АЕ и BF.

Ответ: 16 .

20. Ребра АD и ВС пирамиды DABC равны 24 см и 10 см. Расстояние между серединами ребер BD и AC равно 13 см. Найдите угол между прямыми АD и ВС.

Ответ: 90D .

6.Угол между прямой и плоскостью

•Углом между плоскостью и не перпендику-

лярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость.

•0D < (a;α) <90D .

•Угол между взаимно перпендикулярными прямой и плоскостью равен 90D .

•Если прямая параллельна плоскости (или лежит в ней), то угол между ними считается рав-

ным 0D .

Угол между прямой l и плоскостью α можно вычислить:

1)если этот угол удается включить в прямоугольный треугольник в качестве одного из острых углов;

2)по формуле sin ϕ = sin (l;α)= ρ(AMM ;α), где

M l , l ∩α = A;

3) по формуле

sin ϕ =

или в координат-

ной форме

x1 x2 + y1 y2 + z1 z2

sin ϕ =

, где

+ y2

+ z2

+ y 2

+ z2

n(x1 ; y1 ; z1 )- вектор нормали плоскости α , p(x2 ; y2 ; z2 )- направляющий вектор прямой l;

• прямая l и плоскость α параллельны тогда и только тогда, когда x1 x2 + y1 y2 + z1 z2 = 0 ;

4)используя векторный метод;

5)используя координатно-векторный метод;

6)используя ключевые задачи.

Пример 6. В правильной треугольной призме ABCA1 B1C1 , все ребра которой равны 1, найдите

угол между прямой АВ1 и плоскостью АА1С1С . Решение. Пусть D – середина А1С1 , тогда B1 D - перпендикуляр к плоскости АА1С1С , а D – проекция точки В1 на эту плоскость (рис. 5).

Если ϕ - искомый угол, то sin ϕ = B1 D , где

AB1

AB1 = 2 , B1 D = 23 , и поэтому sinϕ = 46 ,

ϕ = arcsin 46 .

Рис. 5

Ответ: arcsin 46 .

1 / 31 2 3 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.05.201599.73 Кб5Жгучая тайна.docx
#
01.05.201516.44 Кб39Женевские конвенции о защите жертв войны.docx
#
01.05.201540.41 Кб13Женечка сучка.docx
#
01.05.201516.26 Кб12жизнь.docx
#
01.05.201556.68 Кб11Заговор.docx
#
01.05.2015519.9 Кб7задания c1 c2.pdf
#
01.05.2015253.51 Кб19задания c3.pdf
#
28.08.201973.41 Кб1задания бланки.docx
#
22.11.2018233.47 Кб6задания по трудовому праву!.doc
#
01.05.201532.77 Кб105Задания_законы сохранения.doc
#
17.08.2019246.92 Кб6задачи для 3 курса.docx