Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Смоленский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

задания c1 c2

.pdf

Скачиваний:

Добавлен:

01.05.2015

Размер:

519.9 Кб

Скачать

☆

<<< < Предыдущая 12 / 32 3 > Следующая >>>

Ответ:

10. В

В кубе

ABCDA1 B1C1 D1 найдите угол между

прямой AВ1

и плоскостью ABC1 .

Ответ: 30D .

В кубе

ABCDA1 B1C1 D1 найдите тангенс угла

между прямой AA1

и плоскостью BC1 D .

Ответ:

В кубе

ABCDA1 B1C1 D1 найдите тангенс угла

между прямой AC1

и плоскостью BCC1 .

Ответ:

ABCDA1 B1C1 D1 точка Е – середина

В кубе

ребра A1 В1 . Найдите синус угла между прямой

АЕ и плоскостью ВDD1 .

Ответ:

ABCDA1 B1C1 D1 точка Е – середина

В кубе

ребра A1 В1 . Найдите синус угла между прямой

АЕ и плоскостью ВDC1 .

Ответ:

прямоугольном

параллелепипеде

ABCDA1 B1C1 D1 найдите угол между плоскостью

AA1C и прямой

A1 В, если

AA1 = 3 ,

AB = 4 ,

BC = 4.

Ответ: arcsin

2 2

прямоугольном

параллелепипеде

ABCDA1 B1C1 D1 найдите угол между плоскостью

A1 BC и прямой

BC1 , если

AA1 = 8 ,

AB = 6 ,

BC =15 .

Ответ: arcsin 8524 .

8.В прямоугольном параллелепипеде

ABCDA1 B1C1 D1 , у которого AA1 = 4 , A1 D1 = 6 ,

C1 D1 = 6 найдите тангенс угла между плоскостью ADD1 и прямой EF, проходящей через середины ребер АВ и B1C1 .

Ответ: 53 .

9.В прямоугольном параллелепипеде

ABCDA1 B1C1 D1 , у которого AB = 4 , BC = 6 , CC1 = 4 найдите тангенс угла между плоскостью АВС и прямой EF, проходящей через середины ребер AA1 и C1 D1 .

1 . 10

правильной треугольной призме ABCA1 B1C1 , все ребра которой равны 1, точка D

– середина ребра A1 В1 . Найдите синус угла между прямой АD и плоскостью BСC1 .

Ответ:		15		.
Ответ:				.
		10
11. В основании прямой призмы							MNKM1 N1 K1
лежит прямоугольный треугольник MNK, у ко-
торого угол				N равен 90D , угол			M равен 60D ,
NK =18 .		Диагональ боковой грани						M1 N со-
ставляет угол 30D с плоскостью							MM1 K1 . Най-
дите высоту призмы.
Ответ: 6 6 .
12. В основании прямой призмы ABCA1 B1C1 ле-
жит прямоугольный треугольник							АВС, у кото-
рого угол			С		равен 90D , угол		А	равен 30D ,
AC =10		3 . Диагональ боковой грани B1C со-
ставляет угол 30D с плоскостью AA B . Найдите
высоту призмы.							1	1
высоту призмы.
Ответ: 10 2 .
Критерии:
	Содержание критерия						Баллы
	Обоснованно получен					вер-		2
	ный ответ.							2
	ный ответ.
	Способ			нахождения		иско-
	мой величины верен, но по-							1
	лучен	неверный ответ или						1
	лучен	неверный ответ или
	решение не закончено.
	Решение				не соответствует
	ни одному из критериев, пе-							0
	речисленных выше.

13. В правильной шестиугольной призме ABCDEFA1 B1C1 D1 E1 F1 , все ребра которой равны

1, точка G – середина ребра A1 В1 . Найдите синус угла между прямой АG и BСС1 .

Ответ: 1015 .

14. В правильной шестиугольной призме ABCDEFA1 B1C1 D1 E1 F1 , все ребра которой равны

1, точка G – середина ребра A1 В1 . Найдите синус угла между прямой АG и BDD1 .

Ответ: 55 .

15. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите ко-

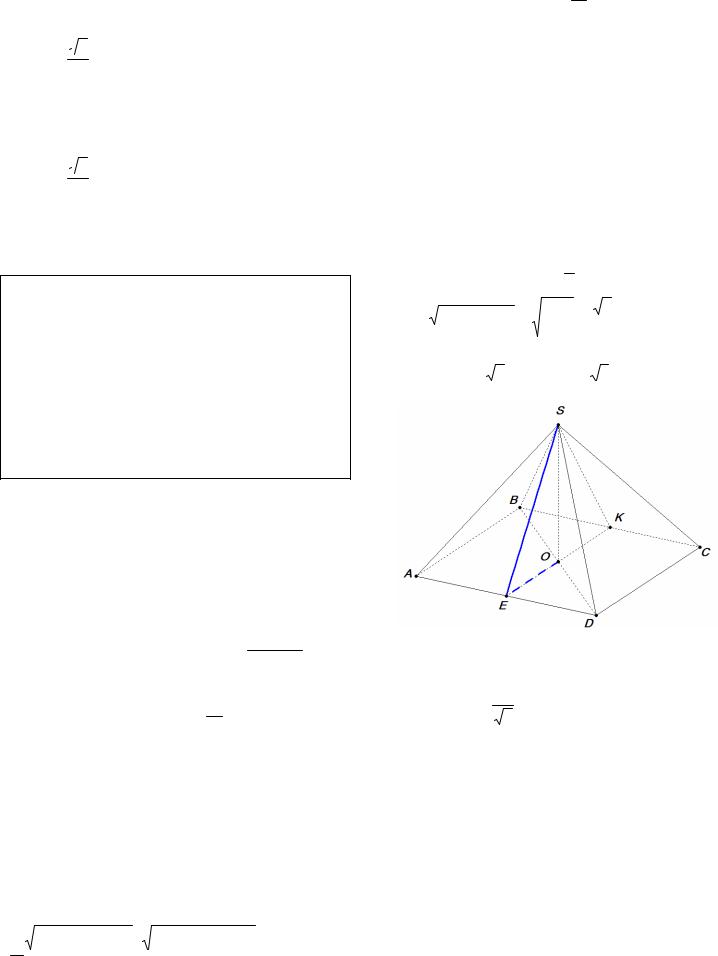
синус угла между прямой АВ и плоскостью

SAD.

Ответ: 33 .

16. В правильной шестиугольной пирамиде SABCDEF, боковые ребра которой равны 2, а стороны основания – 1, найдите косинус угла между прямой АС и плоскостью SAF.

Ответ: 55 .

7.Угол между плоскостями

•Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру.

•Величина двугранного угла принадлежит

промежутку (0D;180D ).

•Величина угла между пересекающимися плоскостями принадлежит промежутку (0D;90D ].

•Угол между двумя параллельными плоско-

стями считается равным 0D .

Угол между пересекающимися плоскостями можно вычислить:

1)как угол между прямыми, лежащими в этих плоскостях и перпендикулярными к линии их пересечения;

2)как угол треугольника, если удается включить линейный угол в некоторый треугольник;

3)по формуле (M ; β), где

ρM ;lsin (α; β)= ρ ( )

M α; α ∩β = l ;

4) по формуле cos (α; β)= SS′ , где S – площадь

фигуры Ф, расположенной в плоскости α , S′ - площадь проекции фигуры Ф на плоскость β ;

5) как угол между перпендикулярными им прямыми;

6) по формуле cos (α; β)=

или в коор-

cos (α; β)

динатной форме

A1 A2 + B1 B2 +C1C2

где

+ B2

+C2

A2 + B

+C2

n1 (A1 ; B1 ;C1 ) - вектор нормали плоскости

A1 x + B1 y +C1 z + D1 = 0 , n2 (A2 ; B2 ;C2 ) - вектор нормали плоскости A2 x + B2 y +C2 z + D2 = 0 ; 7) используя ключевые задачи.

Пример 7. В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1, найдите двугранный угол между основанием и боковой гранью.

Решение. Пусть Е и К – середины ребер AD и BC соответственно, О – центр основания ABCD (рис. 6). Тогда SE AD , EK AD и поэтомуSEK =ϕ - линейный угол данного двугранно-

го угла.

Так как AD =1, OE = 12 , SD =1, то

SE = SD2 − ED2 =						1 −	1	=	3		,
							4		2
		OE
cosϕ	=		=	1	, ϕ = arccos				1	.
		SE		3					3

Рис. 6

Ответ: arccos 13 .

1. Дан куб ABCDA1 B1C1 D1 . Найдите угол между плоскостями AB1C1 и A1 B1C .

Ответ: π3 .

2. Диагональ A1C куба ABCDA1 B1C1 D1

служит ребром двугранного угла, грани которого проходят через середины ребер АВ и DD1 . Найдите величину этого угла.

Ответ: 120D .

3. Диагональ A'C куба ABCDA' B'C' D' служит ребром двугранного угла, грани которого проходят через В и D . Найдите величину этого угла.

Ответ: 120D .

4. В кубе ABCDA1 B1C1 D1 точки Е, F – середины ребер соответственно A1 В1 и A1 D1 . Найдите тангенс угла между плоскостями АЕF и ВCC1 .

Ответ: 25 .

5. В кубе ABCDA1 B1C1 D1 точки Е, F – середины ребер соответственно A1 В1 и A1 D1 . Найдите тангенс угла между плоскостями АЕF и ВDD1 .

Ответ:	2	.
	4

6. В прямоугольном параллелепипеде
ABCDA1 B1C1 D1 известны длины ребер:						AA1 = 5,
AB =12,	AD = 8.				Найдите тангенс угла между
плоскостью				АВС	и плоскостью, проходящей
через точку				В перпендикулярно прямой АК,
если К - середина ребра C1 D1.
Ответ: 2.
7. В прямоугольном параллелепипеде
ABCDA1 B1C1 D1 , у					которого AB = 4 ,	BC = 6 ,
CC1 = 4	найдите				тангенс угла между плоско-
стями CDD1 и BDA1 .
Ответ:	3 2		.

	2
8. В прямоугольном параллелепипеде
ABCDA1 B1C1 D1 , у					которого AB = 6 ,	BC = 6 ,
CC1 = 4	найдите				тангенс угла между плоско-
стями ACD1				и A1 B1C1 .

Ответ: 2 32 .

9. Основание прямой четырехугольной призмы ABCDA1 B1C1 D1 - прямоугольник ABCD , в кото-

ром АВ = 5 , AD =	33 . Найдите тангенс угла
между плоскостью	грани AA1 D1 D призмы и

плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1 D , если рас-

стояние между прямыми A1C1 и BD равно 3 .

Ответ: 1,2.

10. Основание прямой четырехугольной призмы ABCDA1 B1C1 D1 - прямоугольник ABCD , в кото-

ром АВ =12 , AD = 31 . Найдите тангенс угла между плоскостью основания призмы и плоскостью, проходящей через середину ребра AD перпендикулярно прямой BD1 , если расстояние

между прямыми AC и B1 D1 равно 5.

Ответ: 42 .

11. Сторона основания правильной треугольной призмы ABCA1 B1C1 равна 2, а диагональ боко-

вой грани равна 5 . Найдите угол между плоскостью A1 BC и плоскостью основания призмы.

Ответ: 30D .

12. В правильной треугольной призме ABCA1 B1C1 , все ребра которой равны 1, найдите угол между плоскостями

ACВ1 и A1С1 В.

Ответ: arccos 17 .

13. (Демо 2010) Сторона основания правильной

треугольной призмы				ABCA1 B1C1 равна 2, а диа-
гональ боковой грани равна						5 . Найдите угол
между плоскостью				A1 BC и плоскостью основа-
ния призмы.
Ответ: 30D .
14.	В	правильной			треугольной			призме
ABCA1 B1C1 , все ребра которой равны 1, точки D,
Е – середины ребер соответственно A1 В1								и А1C1 .
Найдите тангенс угла между плоскостями АDЕ
и ВCC1 .
Ответ:		3	.
		4

15. Основанием прямой треугольной
призмы ABCA1 B1C1 является равнобедренный
треугольник АВС,				в	котором		AB = BC =10,
AC =16. Боковое ребро призмы равно 24. Точка
Р – середина ребра BB1 . Найдите тангенс угла
между плоскостями				A1 B1C1		и АСР.
Ответ: 2.
16. Основанием прямой треугольной
призмы ABCA1 B1C1 является равнобедренный
треугольник АВС,				в	котором		AB = BC = 20,
AC = 32. Боковое ребро призмы равно 24. Точка
Р	принадлежит			ребра		BB1 ,		причем
BP : PB1		=1 : 3. Найдите тангенс					угла	между

плоскостями A1 B1C1 и АСР.

Ответ: 0,5.

17. Основанием прямой треугольной

призмы ABCA1 B1C1 является треугольник АВС, в котором AB = AC = 8, а один из углов равен 60D . На ребре AA1 отмечена точка Р так, что AP : PA1 = 2 :1. Найдите тангенс угла между плоскостями АВС и СВР, если расстояние между прямыми АВ и C1 B1 равно 18 3 .

Ответ: 3.

18. Основанием прямой треугольной

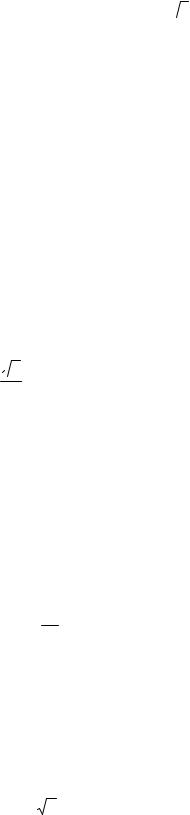
призмы ABCA1 B1C1 является треугольник АВС, в котором AC = BC = 6, а один из углов равен 60D . На ребре CC1 отмечена точка Р так, что CP : PC1 = 2 :1. Найдите тангенс угла между плоскостями АВС и АВР, если расстояние между прямыми АС и A1 B1 равно 18 3 .

Ответ: 4.

19. Основанием прямой призмы

ABCA1 B1C1 является прямоугольный треугольник АВС с гипотенузой АС. Найдите тангенс угла между плоскостью A1 B1C1 и плоскостью, проходящей через середину ребра AA1 и пря-

мую ВС, если AB = 4,	BB1 =12.
Ответ: 1,5.
20. Основание пирамиды DABC - равнобедрен-
ный треугольник	АВС, в котором

AB = BC =13, AC = 24. Ребро DB перпендику-

лярно плоскости основания и равно 20. Найдите тангенс двугранного угла при ребре АС.

Ответ: 4.

21. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите косинус угла между плоскостями АВС и BCS.

Ответ: 33 .

22.Диаметр окружности основания цилиндра равен 20, образующая цилиндра равна 28. Плоскость пересекает его основания по хордам длины 12 и 16. Найдите тангенс угла между этой плоскостью и плоскостью основания цилиндра.

Ответ: 2 или 14.

23.Диаметр окружности основания цилиндра равен 26, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 24 и 10. Найдите тангенс угла между этой плоскостью и плоскостью основания цилиндра.

Ответ: 3 или 1721 .

8.Разные задачи

1.Найдите радиус сферы, внутри которой расположены четыре шара радиуса r. Каждый из этих шаров касается трех других и поверхности сферы.

		6
Ответ: r 1	+		.
Ответ: r 1	+		.
		2
		2

2. Три сферы, попарно касаясь друг друга, касаются плоскости треугольника в его вершинах. Найти радиусы сфер, если

стороны треугольника равны а, b и с.

Ответ:			ab	;	bc	;	ac	.
					2a
			2c				2b
3. Плоскость пересекает боковые ребра									SA, SB
и	SC	треугольной пирамиды SABC							в точках
K,	L и	M соответственно. В каком отношении

делит эта плоскость объем пирамиды, если из-

вестно,	что			SK	=	SL	= 2 , а медиану SN тре-
вестно,	что			KA	=	LB	= 2 , а медиану SN тре-
				KA		LB
угольника SBC эта плоскость делит пополам.
Ответ:		8	.
Ответ:	37		.
	37

4. Найти угол при вершине в осевом сечении конуса, если на его поверхности можно провести три попарно перпендикулярные образующие.

		1
Ответ: arccos	−		.
Ответ: arccos	−	3	.
		3

5. Какие значения принимает угол между образующими конуса, если его образующая в два раза больше радиуса основания?

Ответ: (0D;60D ].

9. Координатный метод

Пример 8. В единичном кубе ABCDA1 B1C1 D1 точки Е и К - середины ребер AA1 и CD соответственно, а точка М расположена на диагонали B1 D1 так, что B1M = 2MD1. Найдите рас-

стояние между точками Q и L, где Q – середина отрезка ЕМ, а L – точка отрезка МК такая, что

ML = 2LK.

Решение. Введем прямоугольную систему координат, как указано на рисунке 7. Тогда

	1			1
Е 0;0;		,	К 1;		;0 ,	В (0;1;1) ,	D (1;0;1) . Для
Е 0;0;	2	,	К 1;	2	;0 ,	В (0;1;1) ,	D (1;0;1) . Для
	2			2		1	1

нахождения координат точки М используем

формулу

координат точки,

делящей

отрезок

B1 D1

отношении

2:1.

Имеем

0 + 2 1

1 + 2 0

1 + 2 1

;

;1 . Анало-

1 + 2

1 +

1 + 2

гично получим координаты точки L, делящей

отрезок

МК

отношении

2:1.

Имеем

+ 2 1

+ 2

1 + 2 0

;

Коор-

1 + 2

динаты точки Q равны полусуммам соответст-

вующих

координат

точек Е и

М,

поэтому

1 +1 +1

ρ(А1 ; β)=

0 +0 −1 −1

А1 (0;0;1)

ние от точки

	1			1			3
Q			;		;			. Применим формулу для расстояния
Q	3		;	6	;		4	. Применим формулу для расстояния
	3			6			4
между точками с заданными координатами
QL =					1					8	2	1		4	2	3		1	2
								−				+	−			+	−		=
							3	−		9		+	−	9		+	−	3	=
							3			9		6		9		4		3
=		725				=			5 29			.
	362									36

Рис. 7

Ответ: 5 3629 .

Пример 9. В единичном кубе ABCDA1 B1C1 D1 найдите расстояние от точки А1 до плоскости

BDC1 .

Решение. Составим уравнение плоскости, проходящей через точки B(0;1;0) , D(1;0;0) и

C1 (1;1;1) . Для этого подставим координаты этих

точек в общее уравнение плоскости

Ax + By +Cz + D = 0 . Получим систему уравнений

B + D = 0			B = −D
		или		Отсюда нахо-
A + D = 0		или	A = −D	Отсюда нахо-
	+ D = 0
A + B +C	+ D = 0		C = D

дим уравнение − Dx − Dy + Dz + D = 0 или

x + y − z −1 = 0 . По формуле находим расстоядо плоскости β = BDC1 :

= 23 .

Рис. 8

Ответ: 23 .

10. Координатно-векторный метод

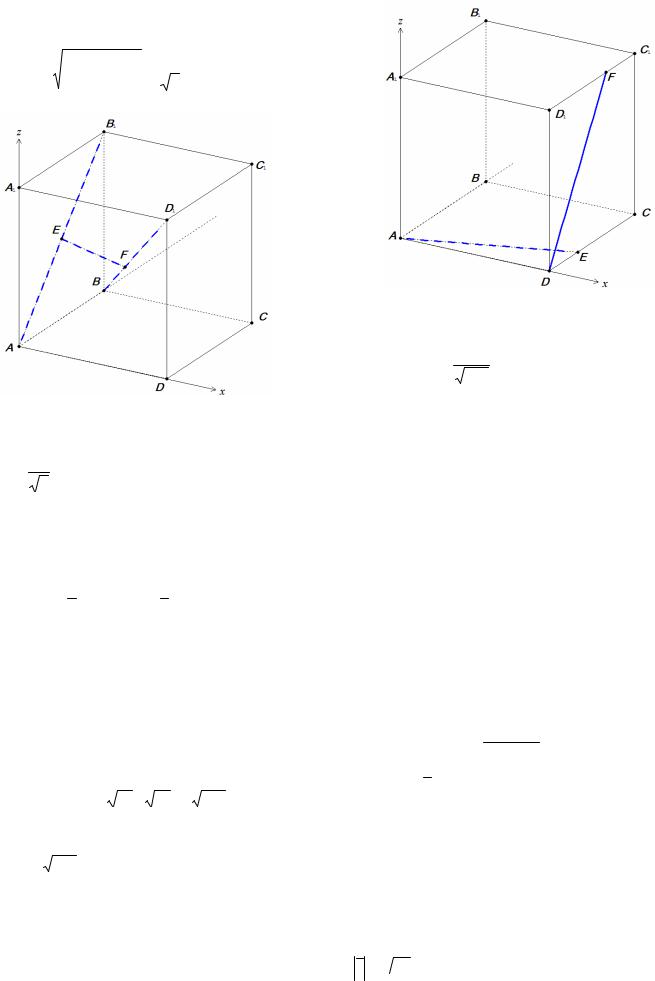
Пример 10. В единичном кубе ABCDA1 B1C1 D1 найдите расстояние между диагональю куба BD1 и диагональю грани AB1 .

Решение. Введем прямоугольную систему координат (рис. 9), тогда

А(0;0;0) , В(0;1;0) ,				В1 (0;1;1) , D1 (1;0;1) .
Пусть EF – общий перпендикуляр скрещиваю-
щихся прямых BD1				и AB1 , то есть EF AB1 ,
EF BD1 , причем E AB1 и F BD1 . Обозна-
чим λ =	AE	, μ =		BF	и воспользуемся фор-
	B E
			D F
1				1

мулами для координат точки, которая делит данный отрезок в заданном отношении. Полу-

чим E 0;

;

, F

;

1 +λ 1 + λ

+ μ 1

+ μ

1 +

Пусть

= p ,

= q , тогда

E(0; p; p) ,

1 + μ

F(q;1 −q; q) . Так как вектор

EF = (q; 1 −q − p; q − p) должен быть перпендикулярным векторам AB1 = (0;1;1) и

BD1 = (1; −1; 1) , то имеем систему уравнений:

= 0

1 −q − p + q − p = 0

или

= 0

q −1

+ q + p + q − p

= 0

p =

q =


					1		1			1
					1		1			1
Отсюда EF =						;		; −				,
Отсюда EF =					3	;	6	; −		6		,
					3		6			6
				1			1				1			1	.
EF =		=			+				+				=
	EF
	EF		9				36			36				6
			9				36			36				6

Рис. 9

Ответ: 16 .

Пример 11. В единичном кубе ABCDA1 B1C1 D1 найдите угол между прямыми АЕ и DF, где Е и F – точки, расположенные на ребрах CD и C1 D1

так, что DE = 13 DC , C1 F = 13 C1 D1 .

Решение. Введем прямоугольную систему координат, как указано на рисунке 10. Тогда

	А(0;0;0) , D(1; 0; 0) ,											1				2
										Е 1;			; 0 , F 1;				;1 ,
										Е 1;		3	; 0 , F 1;			3	;1 ,
												3				3
		1										2
		1										2
	AE = 1;			; 0	, DF				= 0;				;1 ,
	AE = 1;	3		; 0	, DF				= 0;			3	;1 ,
		3										3
												2
			AE DF									2			2
cosα =			AE DF					=				9		=	2			,

											10		13		130

		AE				DF
									3				3
					2				3				3
α = arccos					2		, где α - искомый угол.
α = arccos							, где α - искомый угол.
				130

Рис. 10

2 Ответ: arccos 130 .

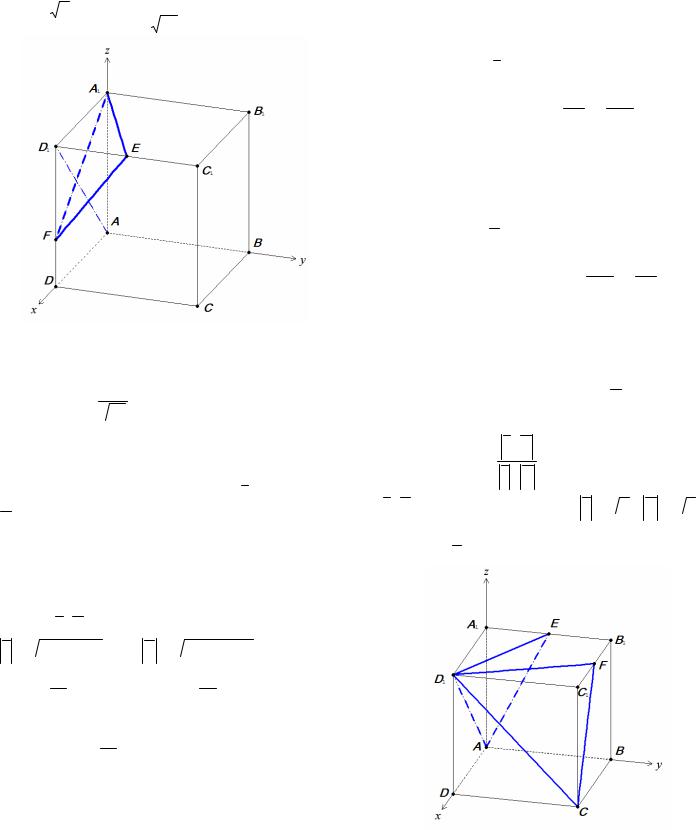
Пример 12. В единичном кубе ABCDA1 B1C1 D1 найдите угол между прямой АD1

иплоскостью α, проходящей через точки А1 , Е

иF, где точка Е – середина ребра C1 D1 , а точка F лежит на ребре DD1 , так, что D1 F = 2DF .

Решение. Введем прямоугольную систему координат, как указано на рисунке 11. Тогда

	А(0;0;0) ,				А1 (0; 0;1) ,						D1 (1; 0;1) ,					1
														Е 1;				;1 ,
														Е 1;		2		;1 ,
																2
		1														1
		1					АD = (1; 0;1),						A E =			1
	F 1; 0;		,												1;		; 0 ,
	F 1; 0;		,												1;	2	; 0 ,
		3						1					1			2
					2
	А1 F =			−	2						n = (x; y; z)
		1; 0;				.		Пусть						-	вектор,
		1; 0;				.		Пусть						-	вектор,
					3
перпендикулярный плоскости α,													ϕ -		искомый

угол. Тогда sin ϕ									=	AD1	n	.


										AD	n
									1

Вектор n найдем из условий перпендикулярности этого вектора векторам

A1 E и А1 F , т.е. из условий

x +

= 0

y = −2x

n A E = 0

или

Пусть

A F

= 0

z =1,5x.

z = 0

x −

x = 2 ,

тогда y = −4 ,

z = 3

= (2; −4;3) ,

n = 29 .

формулу cosϕ =


Так			как	AD1		n	=1 2 +0 (−4) +1 3 = 5 ,
		=	2 , то sin ϕ =		5			.
	AD				5
	AD
	1			58
				58

Рис. 11

Ответ: arcsin 5 . 58

Пример 13. Найдите угол между плоскостями

2x +3y +6z −5 = 0 и 4x + 4 y + 2z −7 = 0 .

Решение. Рассмотрим векторы n = (2;3; 6) и m = (4; 4; 2) , перпендикулярные к данным плос-

костям.			Искомый угол найдем по формуле

cosϕ =		n		m	.


	n			m

Так как n m = 2 4 +3 4 + 6 2 = 32 ,

n = 4 +9 +36 = 7 , m = 16 +16 + 4 = 6 , то cosϕ = 1621 , откуда arccosϕ = 1621 .

Ответ: arccos 1621 .

Пример 14. В единичном кубе ABCDA1 B1C1 D1 найдите угол между плоскостями AD1 E и

D1 FC , где точки Е и F – середины ребер А1 В1 и В1С1 соответственно.

Решение. Введем прямоугольную систему координат, как указано на рисунке 12. Тогда

А(0; 0; 0) , С(1;1; 0) , D1 (1; 0;1) ,		1
	Е 0;		;1 ,
	Е 0;	2	;1 ,
		2

1					1
			АD1 = (1; 0;1),
F		;1;1 ,		AE = 0;		;1 ,
	2				2

			1

СD1	= (0; −1;1), СF =	−		; 0;1 .
			2

Найдем вектор n = (x; y; z) , перпендикулярный плоскости AD1 E . Этот вектор должен быть перпендикулярным векторам AE и АD1 и поэтому

= 0

+ z = 0

y = −2z

n AE

= 0

n AD

x = −z.

+ z = 0

Пусть z = −1, тогда x =1,

y = 2 и

= (1; 2; −1) .

Найдем вектор m = (x; y; z) , перпендикулярный плоскости D1 FC . Этот вектор должен быть

перпендикулярным векторам СD1 и СF и поэтому

− y + z = 0

m CD

= 0

y = z

−

+ z = 0

x = 2z.

= 0

m CF

Пусть z =1, тогда x = 2 , y =1 и m = (2;1;1) .

Для нахождения искомого угла ϕ используем

n m

n m . Так как

n m =1 2 + 2 1 + (−1) 1 = 3 , n = 6 , m = 6 ,

то cosϕ = 12 , откуда ϕ = 60D .

Рис. 12

Ответ: 60D .

11. Векторный метод

Пример 15. В единичном кубе

ABCDA1 B1C1 D1

на диагоналях граней AD1

и D1 B1

взяты точки Е

и F так, что D E =

AD ,

D F =

D B . Найди-

те длину отрезка EF.

Решение. Пусть

(рис.

AA1

=1,

= 0 .

1), тогда

Выразим вектор FE через базисные векторы a ,

b , c :

FE = EA + AB1 + B1 F = − 23 (a + c)+ (b +c)+ 13 (a −b)= = −13 a + 23 b + 13 c . Тогда

						2					1		2		1		2	1		4		1
	FE	=		FE					=	−		a +		b +		c	=		+		+		=
	FE	=		FE					=	−	3	a +	3	b +	3	c	=	9	+	9	+	9	=

=		6	=	6			.
		6		6
		9
		9		3
Ответ:					6			.
Ответ:								.
				3

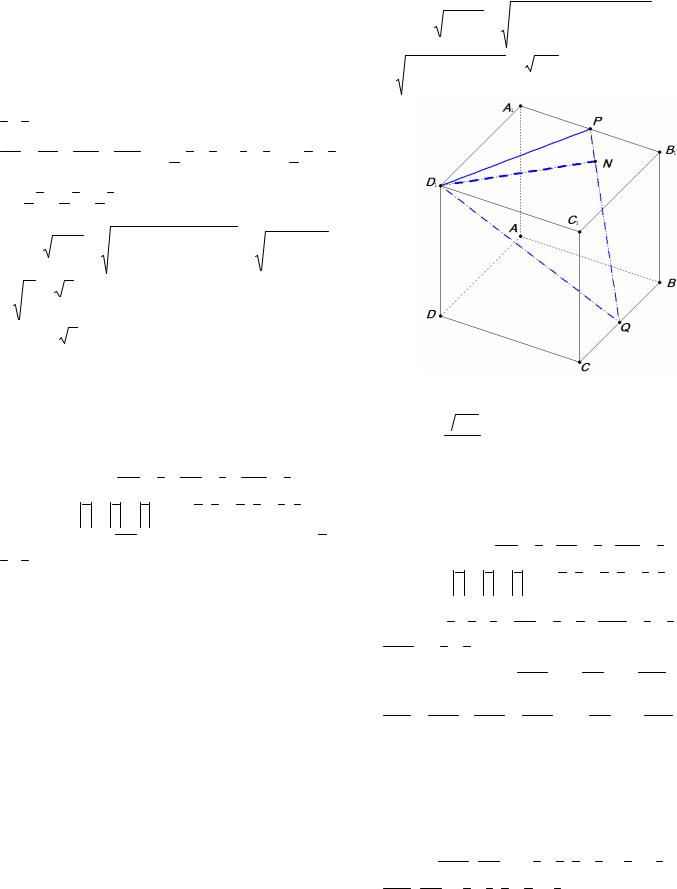
Пример 16. В единичном кубе ABCDA1 B1C1 D1 найдите расстояние от точки D1 до прямой РQ, где Р и Q – середины соответственно ребер

A1 B1 и ВС.

Решение. Пусть AD = a , AB = b , AA1 = c (рис. 1), тогда a = b = c =1, a b = a c = b c = 0 .

Выразим вектор PQ через базисные векторы a ,

b , c :

−

B B

= −

Пусть

D N PQ ,

где

N PQ .

Выразим вектор

D1 N

, учитывая кол-

линеарность

векторов

−

= x

−

Так

как

D1 N

PD1

, то

= 0 . Отсюда получаем

D1 N

−

)

= 0 , x

2 =

PD1

b −c

−

b + a

a +

b −c ,

−

х =

						1																1 1				1						1
	D1 N =					1		PQ					− PD1 =									1 1		а +		1					+	1	b	−a =
	D1 N =					6		PQ					− PD1 =										2	а +		2		b −c			+	2	b	−a =
						6																6	2			2						2
= −			11				+				7			−			1			.
			11		a						7	b					1	c
		12			a				12			b				6		c
		12							12							6
Длина вектора
													2									11			7				1		2
	D1 N			=					D1 N				2			=					−	11	a	+	7		b −		1	c	2	= .

																						12			12				6


=			121			+				49			+			1			=			174		.
		144							144						36							12

Рис. 13

Ответ: 12174 .

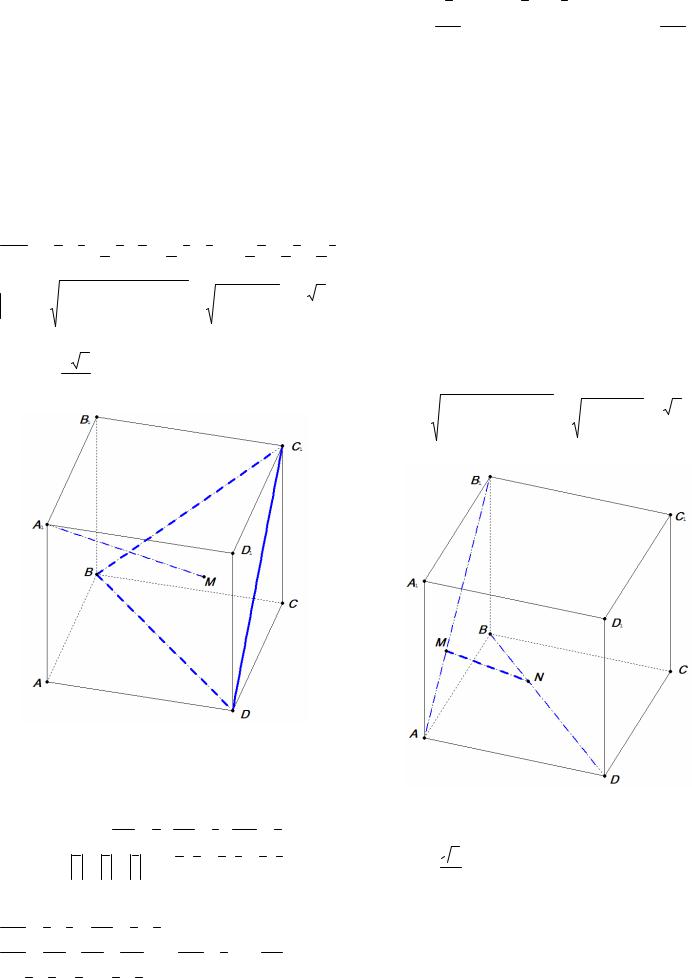
Пример 17. В единичном кубе ABCDA1 B1C1 D1 найдите расстояние от точки А1 до плоскости

BDC1 .

Решение. Пусть AD = a , AB = b , AA1 = c (рис. 14), тогда a = b = c =1, a b = a c = b c = 0 .

Выразим некоторые векторы через базисные векторы a , b , c : DB = b − a , DC1 = b +c , C1 A1 = −a −b . Пусть МА1 BDC1 , где

M BDC1 . Вектор C1M = x DB + y DC1 , поэтому

MA1 = C1 A1 −C1M = C1 A1 −(x DB + y DC1 ).

= 0

Далее имеем

DC1

DC1 = 0

MA1

DB −(x DB

+ y DC1

DB)= 0

C1 A1

−(x

+ y

2 )= 0

C1 A1

DC1

Так как C1 A1 DB = (−a −b)(b −a)= a2 −b2 = 0 , DC1 DB = (b +c)(b −a)= b2 =1,

= (

)(−

−

)= −

2 = −1 ,

DC1

C1 A1

2 =

(

−

)2 =

2 +

2 = 2 ,

2 = (

)2 =

= 2 , то имеем

DC1

0 −(x 2 + y 1) = 0

2x + y = 0

−(x 1 + y 2) =

+ 2 y = −1

−1

x =

y = −

Отсюда получаем

MA1 = −a −b − 13 (b −a)+ 32 (b + c)= − 23 a − 23 b + 32 c

			2		2		2		2	4		4		4		2 3
MA1	=	−		a −		b +		c	=		+		+		=
MA1	=	−	3	a −	3	b +	3	c	=	9	+	9	+	9	=	3

Ответ: 2 33 .

Рис. 14

Пример 18. В единичном кубе ABCDA1 B1C1 D1 найдите расстояние между прямыми AB1 и BD . Решение. Пусть AD = a , AB = b , AA1 = c (рис. 15), тогда a = b = c =1, a b = a c = b c = 0 .

Если M и N – основания общего перпендикуляра прямых AB1 и BD соответственно, то имеем

AB1 = b +c , DB = b − a ,

MN = MA + AD + DN = x AB1 + a + y DB = = x(b + c)+ a + y(b − a)=

= (1 − y) a +(x + y) b + x c .

Вектор MN перпендикулярен векторам AB1 и

DB , поэтому имеем

= 0

((1 − y) a +(x + y) b + x c)(b +c)= 0

− y) a

+(x + y) b

+ x c)(b −a)= 0

((1

+ x c

= 0

(x + y) b

− y) a +(x + y) b = 0

−(1

2x + y = 0

x = −

x + 2 y −1 = 0

y =

Итак,

(

= −

−

a +

b −

Рис. 15

Ответ: 33 .

Пример 19. В кубе ABCDA1 B1C1 D1 найдите угол между прямыми EF и PQ, где E, F, P, Q – середины ребер DD1 , BC, AA1 и B1C1 соответственно.

Решение. Пусть AD = a , AB = b , AA1 = c (рис. 16), где a = b = c =1, a b = a c = b c = 0 . То-

гда EF = ED + DC +CF = − 12 c +b − 12 a ,

				=						+								+									=							1				+									+	1					, откуда на-
	PQ							PA					A B								B Q													1			c				b							1			a
	PQ							PA					A B								B Q																c				b										a
									1					1			1						1											2													2
ходим																																		2													2
ходим																	1														1											1														1

					PQ EF =														c +b +																					−						c +b −																	=
					PQ EF =												2		c +b +												2			a						−		2				c +b −										2		a					=
																	2														2											2														2
									=			2 −					1			2 −					1							2			=1 −							1				−				1		=				1		,
											b						1		c						1					a												1								1						1
											b						4		c											a												4								4						2
																	4									4																4								4						2
												1											1								2									1						2								2				1					2
												1											1								2									1						2								2				1					2
			PQ				=								c +b					+						a								=									c						+b						+						a				=
			PQ				=					2			c +b					+			2			a								=						4			c						+b						+			4			a				=


																	=					1		+			1 +								1			=						3			,
																	=			4				+			1 +							4				=				2					,
																				4														4								2
													1											1										2						1							2								2				1					2
		EF				=			−							c +b −												a						=											c					+b						+						a			=
		EF				=			−				2			c +b −								2				a						=						4					c					+b						+			4			a			=
																						1

																	=							+			1 +								1			=						3			,
																	=			4				+			1 +							4				=				2					,
																				4														4								2

cosϕ =									PQ						EF					=			1			:			3				=			1			, ϕ = arccos																		1			, где ϕ
																							1						3							1																					1

									PQ						EF								2				2							3																							3

- искомый угол.

Рис. 16

Ответ: arccos 13 .

Пример 20. В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1, найдите угол между прямой DE, где E – сере-

дина апофемы SF грани ASB, и плоскостью

ASC.

Решение. Так как прямая ОD перпендикулярна

плоскости ASC, то вектор OD является вектором нормали плоскости ASC.

Пусть

(рис.

17), где

=1,

= 0 ,

2 cos 60D =

. Тогда

= −

(

−

DE = DA + AF + FE = −a +

b +

−

= −

DE OD =

−a +

b +

a −

= −

2 −

2 +

−

−a +

b +

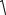= a2 +161 b2 + 14 c2 − 2 12 a c + 2 14 12 b c = = 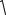1 +161 + 14 − 12 + 18 = 1615 ,

		1			1			2			1		1		1
OD	=		a −			b				=		+		=		,
OD	=		a −			b				=		+		=		,
		2			2						4		4		2
		2			2						4		4		2
sin ϕ =		DE		OD			=		3		4		2 =		3		,
									3		4				3
								8			15				30
		DE		OD				8			15				30

ϕ = arcsin	3	, где ϕ - искомый угол.
	30

Рис. 17

3 Ответ: arcsin 30 .

<<< < Предыдущая 12 / 32 3 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.05.201599.73 Кб5Жгучая тайна.docx
#
01.05.201516.44 Кб39Женевские конвенции о защите жертв войны.docx
#
01.05.201540.41 Кб13Женечка сучка.docx
#
01.05.201516.26 Кб12жизнь.docx
#
01.05.201556.68 Кб12Заговор.docx
#
01.05.2015519.9 Кб7задания c1 c2.pdf
#
01.05.2015253.51 Кб19задания c3.pdf
#
28.08.201973.41 Кб1задания бланки.docx
#
22.11.2018233.47 Кб6задания по трудовому праву!.doc
#
01.05.201532.77 Кб105Задания_законы сохранения.doc
#
17.08.2019246.92 Кб6задачи для 3 курса.docx