§28. Принцип неразличимости одинаковых частиц

 Литература: [1], [8], [3], [7].

Теория возмущения применяется как при анализе движения одной частицы, так и системы частиц – многоэлектронных атомов и молекул.

Системы одинаковых микрочастиц качественно отличаются от системы одинаковых корпускул. Отличие выражается принципом неразличимости и его следствиями. Чтобы понять смысл этого принципа, рассмотрим волновую функцию, описывающую состояние системы N одинаковых микрочастиц. Такая функция должна зависеть от полных наборов B_i, определяющих состояния всех частиц системы:

 =  (B₁, B₂, …, B_i, B_k, …, B_N)  (B_i, B_k). (28.1)

Введем оператор перестановок , который осуществляет преобразование волновой функции системы при обмене состояниями двух частиц (i-ой и k-ой): (B_i, B_k) = (B_k, B_i). (28.2)

Найдем собственные значения оператора перестановок, то есть подберем действительные числа P_ik так, чтобы выполнялось равенство:

(B_i, B_k) = P_ik (B_i, B_k). (28.3)

Применим оператор к равенству (28.3):

² (B_i, B_k) = P_ik² (B_i, B_k). (28.4)

Но, исходя из смысла самого оператора , выражаемого соотношением (28.2), можно утверждать, что двукратное применение этого оператора возвращает функции первоначальный вид:

² (B_i, B_k) = (B_i, B_k). (28.5)

Сравнивая (28.5) и (28.4), приходим к выводу, что P_ik² = 1 и  P_ik = +1 или P_ik = –1. Этим двум возможным собственным значениям оператора соответствуют две собственные функции_s и _a:

P_ik = 1  _s(B_i, B_k) = _s(B_k, B_i) = _s(B_i, B_k) . (28.6)

P_ik = –1  _a(B_i, B_k) = _a(B_k, B_i) = –_a(B_i, B_k) . (28.7)

Волновая функция _s называется симметричной, а _a – антисимметричной.

Может ли система одинаковых микрочастиц описываться волновыми функциями, отличными от рассмотренных собственных функций оператора ? Постулируется, что такого быть не может. Это и утверждаетпринцип неразличимости: система одинаковых микрочастиц может описываться только симметричными или антисимметричными волновыми функциями. И в том, и в другом случаях квадрат модуля -функции не меняется при обмене частиц состояниями. Поэтому состояния системы, получающиеся посредством перестановок частиц, то есть обмена двух частиц своими состояниями, физически неразличимы. Можно сказать, что все частицы в этой системе тождественны, не имеет значения, какая именно конкретная частица оказывается в том или ином состоянии.

Принцип неразличимости согласуется с другими положениями квантовой механики и приводит к экспериментально подтверждаемым следствиям, что доказывает его истинность.

Рисунок 28.1 иллюстрирует согласие принципа неразличимости (тождественности) с корпускулярно-волновым дуализмом. Классические частицы (корпускулы) можно различить, проследив за траекториями их движения: 1A или 2B. Для микрочастиц вместо траекторий можно указать лишь расширяющиеся в пространстве трубчатые области, в которых заметна вероятность обнаружения частиц. Если в точках A и B, принадлежащих обеим указанным трубкам, обнаружены частицы, то невозможно установить, какая из них раньше находилась вблизи точки 1, а какая – вблизи точки 2.

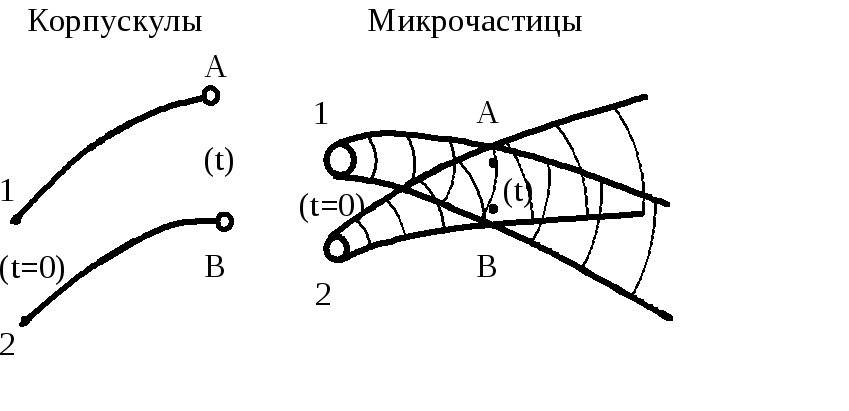Рис. 28.1

Оператор перестановок коммутирует с оператором Гамильтонаи поэтому описывает интеграл движения. Собственное значение интеграла движения должно оставаться неизменным. Следовательно, симметрия волновой функции не может измениться. Частицы, системы которых описываются антисимметричными волновыми функциями, называют фермионами, остальные – бозонами. В. Паули показал, что фермионами являются частицы с полу целыми спинами, а бозонами – с целыми.

Из бозонов могут образовываться только бозоны. Сложная частица, состоящая из четного числа фермионов, оказывается бозоном, в то время частица, содержащая нечетное число фермионов является фермионом.

Из теоремы о разделении переменных (см. §18.) следует, что уравнению Шредингера для системы невзаимодействующих частиц удовлетворяет любая суперпозиция произведений волновых функций отдельных частиц (одно-частичных волновых функций). В качестве волновой функции системы нужно выбрать такие суперпозиции, которые бы обладали необходимой симметрией. Из этих соображений получаются выражения для волновой функции системы N частиц через одночастичные волновые функции _i(B_k). Здесь _i(B_k) – волновая функция k-ой частицы, находящейся в i-ом возможном состоянии. Для системы бозонов получается

_s = , (28.8)

а для системы фермионов –

_a = 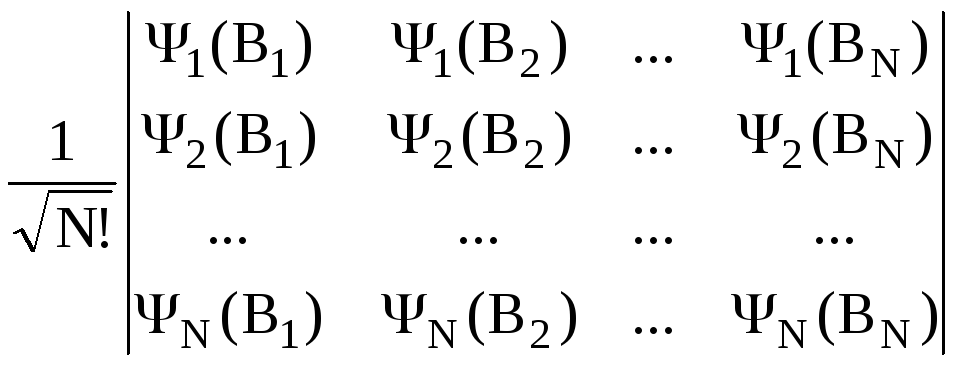. (28.9)

Коэффициент N в этих формулах обеспечивает нормировку функции на единицу. Суммирование в (28.8) проводится по всевозможным перестановкам частиц.

Из (28.9) следует запрет (принцип) Паули: в системе одинаковых фермионов в одном одночастичном состоянии не может быть более одной частицы.

Предположим, что это не так. Пусть, например, есть состояние _a  0, при котором первая и вторая частицы находятся в одном состоянии ₁. Тогда выражение (28.9) должно содержать произведение ₁(B₁) ₁(B₂), что возможно лишь при равенстве двух первых строк определителя. Но такой определитель равен нулю. Это противоречит исходному утверждению _a  0, что и доказывает принцип Паули.

? Контрольные вопросы

1. Сформулируйте принцип неразличимости одинаковых частиц и поясните смысл его названия.

2. Расскажите о связи принципа неразличимости с корпускулярно-волновым дуализмом и с туннельным эффектом.

3. Расскажите о частицах с симметричными и с антисимметричными волновыми функциями.

4. Докажите принцип Паули.