
Пак Г.К. - Дискретная математика
.pdf
f P2 f = C( f1, …), fi = Ci( g1, …) f N2 P2 N2 P2 = N2 .
Упражнение
Докажите полноту классов: , ; , ; , ; 0, ; .
4.2. Классы функций, сохраняющих константы
Булева функция сохраняет константу 0, если на нулевом наборе значений переменных принимает значение 0, сохраняет константу 1, если на единичном наборе значений переменных принимает значение 1. Классы функций, сохраняющих константы, обозначаются соответственно Т0 и Т1. Функции тождественная, конъюнкция и дизъюнкция сохраняют обе константы; отрицание не сохраняет их; сумма по модулю 2 сохраняет 0, но не сохраняет 1; импликация сохраняет 1, но не сохраняет 0.
ТЕОРЕМА. Число всех различных n-местных булевых функций, со-
храняющих константу 0, равно 22n . 2
Доказательство. Разобьем множество всех булевых функций на пары “функция и ее отрицание”. В паре одна и только одна функция сохраняет константу ноль. Следовательно, число всех различных n-местных булевых функций, сохраняющих константу 0, равно половине общего числа всех n-местных булевых функций. Такое же утверждение верно и для функций, сохраняющих константу 1.
ТЕОРЕМА. Классы функций, сохраняющих константы 0 и 1, замкнуты.
Доказательство. Пусть f1(0,…,0) = 0, f2(0,…,0) = 0, f = f1(x1,…, xn –1, f2(y1,…,ym)).
f(0,…,0)) = f1(0,…,0, f2(0,…,0)) = f1(0,…,0) = 0 f T0.
Многократным повторением этого рассуждения можно доказать, что любая суперпозиция функций класса Т0 вновь функция класса T0. Точно также доказывается замкнутость класса T1.
Упражнения
Найдите число всех различных n-местных булевых функций, сохраняющих константы 0 и 1 одновременно. Замкнут ли класс таких функций?
4.3. Класс самодвойственных булевых функций
Если f* = f, то функция f называется самодвойственной. Множество всех самодвойственных булевых функций обозначается через S. Функции х, х самодвойственные. Функции и двойственны друг другу и поэтому несамодвойственные. Два набора из нулей и единиц называем их противоположными, если на соответствующих местах у них расположены противоположные элементы 0 и 1.
41
ТЕОРЕМА. Булева функция самодвойственная тогда и только тогда, когда на противоположных наборах значений переменных принимает противоположные значения.
Доказательство. f* = f f(х1,…, хn) = f( x1 ,…, xn).
ТЕОРЕМА. Число всех различных n-местных самодвойственных буле-
вых функций равно22n 1.
Доказательство. По предыдущей теореме оно равно числу всех возможностей для составления верхней половины таблицы, задающей n-местную булевую функцию.
ТЕОРЕМА. Класс S замкнут.
Доказательство. Пусть f1, f2 S f1(х1, …, хn) = f1( x1, …, xn),
f2(х1, …, хn) = f2( x1, …, xn); f = f1(x1, …, xn–1), f2(y1, …, ym)) f* = f1( х1, …, хn–1, f2( y1, …, ym)) =
= f1( x1, …, xn–1, f2(y1, …,ym))=f1(х1, …,хn-1, f2(y1 ,…,ym))=f f S.
Общий случай можно получить многократным повторением этого рассуждения. ■
Упражнение
Найдите число всех различных n-местных булевых функций, принимающих одинаковые значения на одних и тех же наборах значений переменных. Замкнут ли класс таких функций?
4.4. Класс монотонных булевых функций
Введем на множестве всех n-местных двоичных векторов частичный порядок: вектор = а1,…,аn предшествует вектору = b1, …,bn тогда и только тогда, когда a1 b1,…,an bn . Записываем это так: .
Булева функция называется монотонной, если из того, что предшествует следует, что f( ) f( ), где f( ) = f(a1, …, an). Множество всех монотонных булевых функций обозначим через М. Легко видеть, функции отрицание, сумма по модулю два, эквиваленция и импликация немонотонны, а тождественная функция, конъюнкция и дизъюнкция монотонны.
ТЕОРЕМА. Класс М замкнут.
Доказательство. Пусть f1(х1, …, хn) М, f2(у1, …, уm) M,
a1 b1, …, an + m –1 bn+m –1 f2(an , .., an+m –1) f2(bn, …, bn+m –1).
Рассмотрим функцию f = f1(x1, …, xn –1, f2(y1, …, ym)). Для нее f(a1, …, an+m –1) = f1(a1, …, an –1, f2(an, …, an+m –1)) f1(b1, …, bn –1,
f2 (bn,…, bn+m –1)) = f(b1, …, bn+m –1) f M.
Повторением этого рассуждения можно доказать, что любая суперпозиция функций из М вновь принадлежит М, а это значит, что класс М замкнут. ■
42
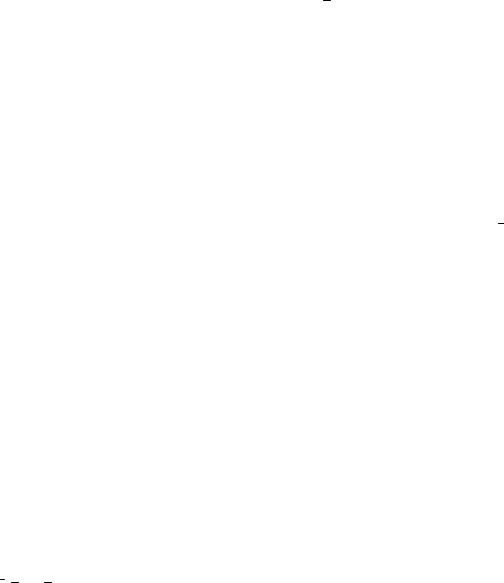
Упражнение
Докажите, что функции Шеффера и Пирса немонотонные, а функция h(x, y, z) = xy xz yz монотонная.
4.5. Класс линейных булевых функций
Сумма по модулю два монотонных элементарных конъюнкций называется полиномом Жегалкина. Наибольший ранг монотонных элементарных конъюнкций, входящих в полином Жегалкина, называется его степенью. Булева функция, представимая в виде полинома Жегалкина степени не выше первой, называется линейной. В соответствии с этим определением константы 0 и 1 отнесем к линейным булевым функциям. Множество всех линейных булевых функций обозначается через L. Этому классу принадлежат тождественная функция, функция отрицания, сумма по модулю два, эквиваленция. Конъюнкция, дизъюнкция, импликация – нелинейные булевы функции. Точно так же, как доказывали ранее, можно доказать следующие теоремы.
ТЕОРЕМА. Число всех различных n-местных линейных булевых функций равно 2n 1.
ТЕОРЕМА. Класс линейных булевых функций замкнут.
Составим таблицу принадлежности элементарных булевых функций к важнейшим замкнутым классам.
Таблица 4.1
|
0 |
1 |
х |
|
|
|
|
|
|
|
|
h |
T0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
T1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
L |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
M |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
S |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
4.6. Три леммы ТЕОРЕМА (лемма о несамодвойственной булевой функции).
Из любой несамодвойственной функции с помощью подстановки в нее вместо переменных тождественной функции и функции отрицания можно получить константу 0 или 1.
Доказательство. Пусть f S f f . Это означает, что найдется набор значений переменных, для которого f (a1, ,an ) f (a1, ,an ), т.е.
|
|
|
|
|
x при ai |
1, |
|||
f (a1, ,an ) f (a1, ,an ). |
Если i (x) |
|
|
ai |
0, 1 i n, |
||||
|
|
|
|
|
x при |
||||
43
то i (0) ai, i (1) ai и для функции (x) f ( i (x), , n (x))от одной переменной х имеем (0) f ( 1(0), , n(0)) f (a1, ,an );
(1) f ( 1(1), , n (1)) f (a1, ,an ), т.е. (0) (1) const .■
ТЕОРЕМА (лемма о немонотонной булевой функции). Из любой немонотонной булевой функции с помощью подстановки в нее вместо переменных констант 0 и 1 и тождественной функции можно получить функцию отрицания.
Доказательство. Пусть f M = a1, …, an , = b1,…, bn , , но f( ) > f( ), т.е. f( )=1, f( ) =0. Неравенствоai <bi, означает, чтоai = 0, bi =1.
ai, если ai bi, Если i (x)
x, если ai bi ,
то i (0) ai, i (1) bi и для функции (x) f ( 1(x), , n(x))имеем
(0) f ( ) 1, (1) f ( ) 0 (x) x. ■
ТЕОРЕМА (лемма о нелинейной булевой функции). Из любой нели-
нейной булевой функции с помощью подстановки в нее вместо переменных констант 0 и 1, тождественной функции, функции отрицания можно получить конъюнкцию или отрицание конъюнкции.
Доказательство. Представление нелинейной булевой функции f в виде полинома Жегалкина содержит слагаемое, в котором обязательно присутствуют конъюнкция каких-либо двух переменных. Изменение нумерации переменных не ослабит общности доказательства теоремы, и мы изменим нумерацию переменных таким образом, чтобы в полиноме Жегалкина присутствовало слагаемое с конъюнкцией х1х2. Тогда, собрав в одну скобку все слагаемые, содержание х1х2, в другую все слагаемые, содержание х1, но не содержащие х2, в третью – содержащие х2, но не содержащие х1, получим
f(x1, ,xn) x1x2 f1(x3, ,xn) x1 f2(x3, ,xn) x2 f3(x3, ,xn) f4(x3, ,xn),
где в силу единственности представления булевой функции в виде полинома Жегалкина f1 0, т.е. существует набор значений переменных, для которого f1(a3, ,an) 1.
Пусть f2(a3, ,an) , f3(a3, ,an) , f4(a3, ,an)(x1,x2) f(x1,x2,a3, ,an) x1x2 x1 x2
(x,y) (x ,y ) xy
(x, y) xy, если 0, или (x, y) (xy), 1. ■
Упражнения
1. Взять произвольно функцию, проверить, является ли она несамодвойственной. Если функция несамодвойственная, то с помощью
44

алгоритма, описанного в доказательстве леммы о несамодвойственной функции, построить константу.
2.Взять произвольно функцию, проверить, является ли она немонотонной. Если функция немонотонная, то с помощью алгоритма, описанного в доказательстве леммы о немонотонной функции, построить отрицание.
3.Взять произвольно функцию, проверить, является ли она нелинейной. Если функция нелинейная, то с помощью алгоритма, описанного в доказательстве леммы о нелинейной функции, построить конъюнкцию или отрицание конъюнкции.
4.7. Теорема Поста о функциональной полноте
ТЕОРЕМА (критерий полноты функциональной системы). Для полноты функциональной системы необходимо и достаточно, чтобы для каждого из пяти важнейших замкнутых классов в ней нашлась функция, ему не принадлежащая.
Доказательство. Пусть N – полный класс и N Т0 N Т0
Р2 Т0 Р2 = Т0. Противоречие. Следовательно, в классе N найдется функция, не сохраняющая константу 0. Аналогично приходим к противоречию, предположив, что полный классN принадлежит классам T1,L, M, S.Предположим, что в классе N найдутся функции f0 Т0 , f1 T1, f2 S,
f3 |
M, f4 L. Так |
как f0(0,…, |
0) = 1, то (x) |
= f0(x,…, |
x) = |
x |
, |
||
если |
f0(1,…,1) = 0, и |
(x) = 1, |
если f0(1,…,1) = |
1. Для |
функции |
||||
(x) f1(x, ,x)имеем |
(x) |
|
, если f1(0, ,0) 0, |
и (x) 1, |
|||||
x |
|||||||||
если f1(0, ,0) 1. С помощью f0 и f1 в N можно получить 0; |
1 или х. |
||||||||
При наличии отрицания с помощью несамодвойственной функции f2 в
N можно построить константу, а следовательно, и вторую константу, т.е. можно построить 0 и 1. При наличии обеих констант с помощью немонотонной функции f3 можно построить отрицание. При наличии обе-
их констант и отрицания с помощью нелинейной функции f можно построить конъюнкцию. При наличии конъюнкции и отрицания с помощью законов де Моргана можно построить дизъюнкцию. Таким образом, в N построен полный класс , , N = Р2 N – полный класс. ■
Следствие. Из любой полной системы можно выделить полную подсистему, содержащую не более четырех функций.
Доказательство. Так как самодвойственная функция на противоположных наборах значений переменных принимает противоложные значения, то f0(1,…,1) = 1 означает, что f0 S. Если же f0(0,…,0) = 1 f0 M. Отсюда вместо пяти разных функций в доказательстве достаточной теоремы можно брать только четыре, которые образуют полную систему. ■
Замечание. Число 4 в следствии не может быть понижено. Из следующей таблицы видно, что четыре функции по теореме Поста образуют полную систему, но после удаления любой из них система перестает быть полной:
|
|
0 |
1 |
|
х1х2 |
x1 х2 х3 |
|
Т0 |
1 |
0 |
|
1 |
1 |
|
Т1 |
0 |
1 |
|
1 |
1 |
|
L |
1 |
1 |
|
0 |
1 |
|
M |
1 |
1 |
|
1 |
0 |
|
S |
0 |
0 |
|
0 |
1 |
|
|
|
Упражнение |
|
|
|
Полны ли системы булевых функций? |
|
|
||||
1) |
, , ; |
|
5) ; |
|
|
|
2) |
, ; |
|
6) ; |
|
|
|
3) |
, , ; |
|
7) , , 1 ; |
|
||
4) |
; |
|
8) , 0 . |
|
|
|
4.8. Предполные классы
Класс булевых функций называется предполным, если он неполный, но при добавлении к нему любой функции, ему не принадлежащей, становится полным. Ясно, что предполный класс замкнут.
ТЕОРЕМА (Поста). Классы T0, T1, L, M , S предполные. Других предполных классов нет.
Доказательство. Если f0 T0, то f0(x, …, x) = 1 или x. В первом случае в T0 f0 появляется полная система 0, 1, , , а во втором тоже полная система , . Отсюда Т0 – предполный класс.
Если f1 T1, то f1(x,…, x) = 0 или x. В первом случае в T1 f1 появляется полная система x = (х 0), , , а во втором та же полная система , , . Отсюда Т1 – предполный класс.
Если f2 S, то по лемме в S f2 появляются 0 или 1, а благодаря отрицанию, обе константы 0 и 1. С помощью h(x, y, z) = xy xz yz и константы 0 можно получить конъюнкцию h(x, y, 0)= ху. Наличие , означает полноту множества S f2 . Отсюда, S – предполный класс. Если f3 M , то по лемме x M f3 . С учетом того, что и функции монотонные, получаем предполноту класса M.
Если f4 L, то по лемме о нелинейной булевой функции можно построить конъюнкцию или отрицание конъюнкции. Так как x L, то, L f4 L – предполный класс.
45 |
46 |
Пусть N – предполный класс, отличный от каждого из важнейших замкнутых классов. По теореме Поста о полноте системы такой класс полный. ■
4.9. Замкнутые классы
Из теоремы Поста следует, что любой замкнутый класс полностью принадлежит одному из важнейших замкнутых классов. Американский математик Эмиль Пост осуществил исследование структуры замкнутых классов в том же плане, в котором было изучено множество Р2.
Система функций из замкнутого класса N называется полной, если ее замыкание совпадает с этим классом N. Система функций из N называется базисом N, если она полна в N и независима. Например, можно показать, что система 0, 1, , – базис класса M. Приведем без доказательства теоремы:
ТЕОРЕМА. Замкнутый класс имеет конечный базис.
ТЕОРЕМА. Замкнутых классов в Р2 счетное число.
|
ГЛАВА 5. ГРАФЫ И СЕТИ |
||
Графом называется пара множеств (V, X), где V – множество |
|||
вершин, а X – некоторое множество неупорядоченных пар i, j эле- |
|||
ментов i и j из V, множество рёбер. Граф называется ориентирован- |
|||
ным (орграфом), если пары i, j упорядочены. В этом случае ребра |
|||
называют дугами. Граф конечен, если множества V, X конечны. Ребро |
|||
вида , |
называется петлёй. Рёбра |
x 1, 2 и y 1, 2 называ- |
|
ются кратными. Договоримся под словом граф подразумевать, если не |
|||
оговорено противное, конечный граф без кратных рёбер и без петель. |
|||
Если в графе существует ребро x a, b , которое соединяет вершины |
|||
а и b, то вершины а и b называют смежными, а вершину а и ребро x – |
|||
инцидентными. Граф называется полным, если в нём любые две верши- |
|||
ны смежны. Полный граф с р вершинами обозначается Kp. Например, |
|||
K2 : |
К3 : |
К4 : |
К5 : |
|
|
|
|
Рис. 5.1 |
|
|
|
5.1. Степень вершины графа |
|
|
|
||||
|
Совокупность рёбер, инцидентных вершине , называется звездой |
||||||
вершины . |
Число рёбер графа, инцидентных вершине , называ- |
||||||
ется степенью вершины ; обозначение deg , т.е. deg = . |
|
||||||
ТЕОРЕМА. Сумма степеней всех вершин графа равна удвоенному |
|||||||
числу его рёбер, т.е. |
2 X deg . |
|
|
|
|||
|
|
|
V |
|
|
|
|
Доказательство. В сумме |
deg каждое ребро учтено дважды. |
||||||
|
|
|
V |
|
|
|
|
|
Если deg |
= 0, то – изолированная вершина. Если deg |
= 1, то |
||||
– концевая вершина. Если все вершины имеют одинаковую степень r, |
|||||||
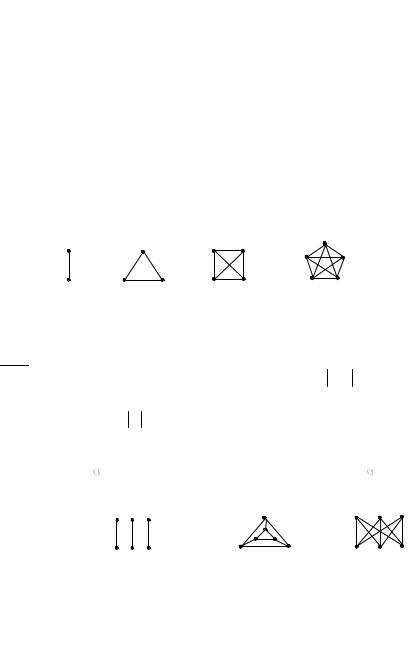
то граф называют регулярным (однородным) степени r. Пример графа |
|||||||
степени |
|
|
|
|
|
|
|
0: . . . ; |
степени 1: |
; |
степени 3: |
; |
Kз.з: |
|
|
|
|
|
|
Рис. 5.2 |
|
|
|
|
|
|
|
Упражнения |
|
|
|
1. В графе число вершин нечётной степени чётно. Докажите это. |
|||||||
2. Докажите, что в любом графе, содержащем не менее двух вершин, |
|||||||
найдутся две вершины одинаковой степени. |
|
|
|
||||
3. Можно ли 7 человек соединить телефонной связью таким образом, |
|||||||
что каждый из них связан ровно с тремя другими? |
|
|
|||||
47 |
48 |
5.2. Способы задания графа
Задать граф – описать множества его вершин и рёбер, а также отношения инцидентности. Для описания конечных графов достаточно перенумеровать вершины и рёбра.
Способ 1. Пусть 1,..., n – вершины графа G, x1, … , xh – рёбра. Отношение инцидентности можно определить матрицей инцидентностиij , имеющей h строк и n столбцов. Если ребро x инцидентно вершине
i , то ij = 1, в противном случае = 0. В матрице инцидентности ij
ориентированного графа G, если вершина j – начало ребра xi, то
ij = 1, а если конец ребра, то +1. Если xi – петля, а j – инцидентная ей вершина, то ij , где – любое число, отличное от 1, 0, 1.
В остальных случаях ij = 0.
Способ 2. Отношение инцидентности можно задать списком рёбер графа. Каждая строка этого списка соответствует ребру, а в ней записаны номера вершин, этому ребру инцидентных.
Способ 3. В матрице смежности графа столбцам и строкам соответствуют вершины графа. Элемент ij этой матрицы равен количеству рё-
бер, инцидентных i-й и j-й вершинам, если в графе допускаются кратные рёбра. Для ориентированного графа этот элемент равен количеству рёбер с началом в вершине i и концом в вершине j.
5.3. Изоморфизм графов
Пусть даны два графаG1 V1, X1 ,G2 V2, X2 . Графы G1 и G2 называются изоморфными, если существуют взаимнооднозначные соответствия между множествами вершин и множествами рёбер этих графов, при этом соответствующие рёбра соединяют соответствую-
щие вершины, т.е. если f :V1 V2 , g : X1 X2 , то
g 1, 2 = f 1 , f 2 .
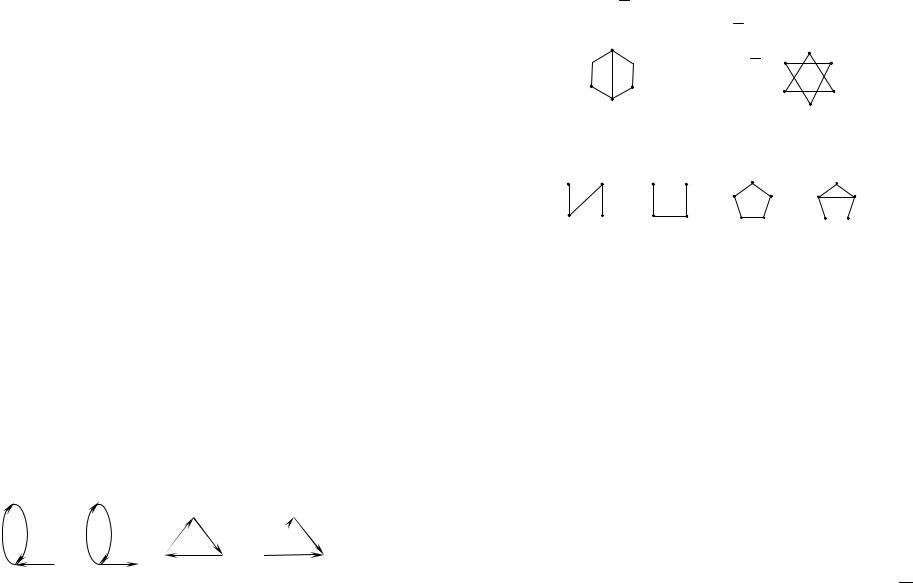
Изоморфизм графов обозначаем G1 G2. Множество всех графов разбивается на непересекающиеся классы изоморфности графов. Пример. Все представители классов изоморфности орграфов с тремя вершинами и тремя рёбрами:
Рис. 5.3
49
Изоморфизм графа на себя называется автоморфизмом графа. Все автоморфизмы графа образуют группу относительно операции композиции отображений.
Дополнение G графа G V, X имеет в качестве множества
вершин множество V, а две вершины в G смежны не смежны в G.
Пример.
G: 
 G :
G :
Рис. 5.4
Самодополнительный граф – это граф, который изоморфен своему дополнению. Наименьшие по числу рёбер нетривиальные самодополнительные графы.
Рис. 5.5
Задача Ремсея. Доказать, что среди шести человек найдутся трое попарно знакомых или попарно незнакомых.
Решение. Шестивершинный граф либо его дополнения содержат треугольник.
Упражнения
1.Разработать порядок перебора и перечислить все попарно неизоморфные трёхвершинные, четырёхвершинные и пятивершинные графы (4; 11; 34).
2.Перечислить все попарно неизоморфные двух-, трех-, четырехреберные графы без изолированных вершин (2; 5; 11).
3.Изоморфны ли графы G1 и G2:
(1) G1: |
14 16 23 25 26 |
45; |
G2: |
16 15 26 24 35 |
34. |
(2) G1: |
12 23 24 15 34 |
45; |
G2: |
12 23 51 25 41 |
34. |
5.4. Подграф, маршрут, цепь, цикл
Граф G V , X называется подграфом графа G V, X , если
V V, X X . Подграф, не совпадающий с графом G и не являющийся пустым, называется собственным подграфом графа G. Подграф, содержащий все вершины графа, называется остовным. Маршрутом (путём) длины называется последовательноcть вершин и рёбер
a0,x1,a2,x2 ,...,a , где ребро xi соединяет вершины ai 1 и ai , i 1, ,
50
a0 – начало пути, a – конец. Если a0 a , то маршрут называется
замкнутым. Если a0 a , то маршрут называется открытым. Откры-
тый маршрут, в котором все вершины различны, называется цепью. Маршрут, в котором все рёбра различны, называется простым. Замкнутый (простой) маршрут называется циклом (простой цикл или элементарный). Если существует маршрут, соединяющий две вершины, то из рёбер этого маршрута можно построить цепь (для этого следует выбрать маршрут минимальной длины из рёбер данного). Длина кратчайшей цепи, соединяющей вершины a и b, называется расстоянием между этими вершинами a,b . Если рёбра a и b не соединены цепью, то
a,b .
Свойства расстояния:
(1) a,b 0, (a,b) 0 a b;
(2)a,b b,a ;
(3)a,b b,c a,c .
Пусть S – некоторое непустое множество вершин V графа G V,X , а
X S – совокупность рёбер графа, обе вершины которых S . Подграф
S,X S графа G называется подграфом, порождённым S.
5.5. Связность
Граф G V,X называется связным, если любые две его различные вершины соединяет цепь. На множестве вершин графа определим отношение a b, если a b или если в графе существует цепь, соеди-
няющая a и b. |
Отношение является отношением эквивалентности. |
|||
Пусть V1,...,Vk |
– классы эквивалентности множества вершин графа |
|||
G V,X , |
определяемые |
этим |
отношением. |
Подграфы |
V1,X V1 ,…, Vk ,X Vk графа G называются компонентами связности
этого графа, а их число называется степенью связности графа. Если граф имеет несколько компонентов связности, то вершины можно перенумеровать так, что егоматрица инцидентности клеточно диагональна.
ТЕОРЕМА. Ранг матрицы инцидентности графа, имеющего компо-
нент связности и n вершин, равен n – .
Доказательство. Достаточно доказать, что ранг матрицы М связного графа c n вершинами равен n – 1. Так как в каждой строке матрицы по две единицы, то сумма всех столбцов по модулю 2 нулевая r M n. Если один столбец матрицы удалить, то в некоторых строках останется по одной единице. Если предположить, что r(M) n – 1, то в столбцах
должно быть чётное число единиц, а это противоречит только что сказанному. ■
В связном графе ребро называется перешейком, если после его удаления из графа свойство его связности исчезает. Связный граф без циклов называется деревом.
5.6. Геометрическая реализация графа
Рассмотрим в трёхмерном пространстве или на плоскости геометрические фигуры, состоящие из точек-вершин и кривых-дуг, каждая из которых соединяет некоторые пары вершин. Эти кривые не имеют общих точек, кроме вершин. Фигура Г называется геометрической реализацией графа G, если Г G. Фигура Г на плоскости называется плоским графом.
ТЕОРЕМА. Каждый конечный граф имеет геометрическую реализацию в трёхмерном пространстве.
Доказательство. Пусть граф G содержит n вершин и h рёбер. Проведём через произвольную прямую h плоскостей. На прямой выберем n точек, которые сопоставим вершинам графа. Каждому ребру графа G сопоставим плоскость из данного пучка плоскостей и в ней проведём соответствующую дугу. ■
Граф называется планарным, если существует его геометрическая реализация на плоскости. Введём операцию подразбиения ребра графа G. Пусть u, – произвольное ребро графа, t V . Операция под-
разбиения ребра u, заключается в построении нового графа с мно-
жеством вершин VU t и множеством рёбер X \ u, u,t , t, .
Граф G2 называется подразбиением графа G1 , если он может быть получен из G1 путём применения конечного числа раз операции подразбиения рёбер. Графы G1 и G2 называются гомеоморфными, если
существуют их изоморфные подразбиения.
Любой планарный граф допускает реализацию в виде плоского графа, у которого все рёбра – отрезки прямых. Часть плоскости, которая ограничена рёбрами плоского графа и не содержит других рёбер, кроме граничных, называется гранью. Для каждого плоского графа имеется внешняя грань.
5.7. Эйлерова характеристика
Эйлеровой характеристикой связного плоского графа G называется число G n h ,
где n – число вершин графа G; h – число его рёбер;
51 |
52 |
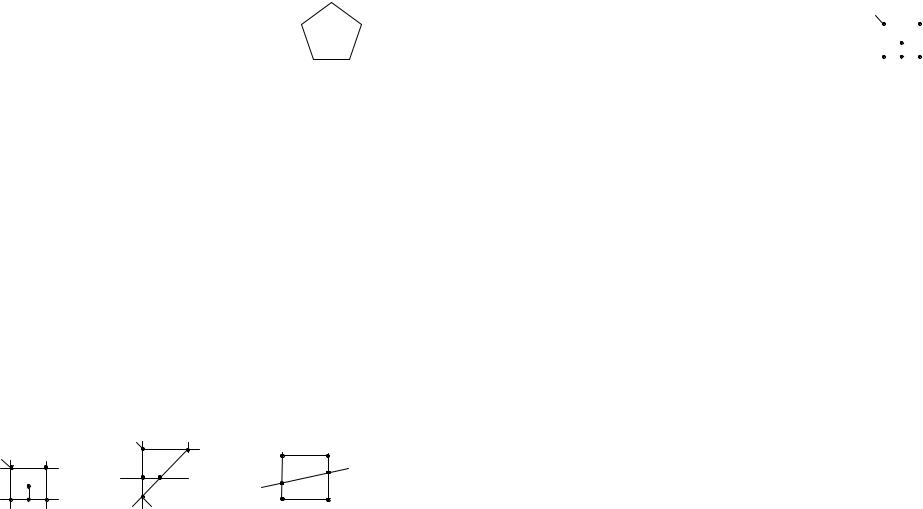
|
|
– число областей, на которые G делит плоскость, |
|
|||||
включая и бесконечную область. Например, для графа, |
|
|||||||
изображённого на рис. 5.6, имеем G 5 5 2 2. |
|
|
||||||
|
|
Пусть даны два графа G и |
|
i , ..., i |
– |
|
||
|
|
G , пусть |
|
|||||
|
|
|
|
|
1 |
k |
|
|
части, на которые дуги графа G |
делят дугу i |
графа |
Рис. 5.6 |
|||||
G, j ,..., j |
определены аналогично. |
Граф |
G |
с |
рёбрами |
|||
..., i |
|
1 |
k j |
|
|
|
|
|
s |
,..., j |
,... называется наложением графов G и G . |
|
|||||
|
t |
|
|
|
|
|
|
|
Лемма 1. Пусть связный плоский граф G получен из связного плоско- |
||||||||
го графа G наложением ребра |
с несовпадающими концами. Тогда |
|||||||
G G . |
|
|
|
|
|
|
||
Доказательство. Очевидно, что пересечение графа G и ребра не пусто, иначе G не мог бы быть связным. Пусть a, b – концы отрезка , а x1, ..., xt – точки пересечения и G.
Случай 1. Ни одна из точек a,b,x1,..., xt не совпадает ни с одной из вершин графа G. Тогда число вершин в графе G равно n n t 2 . Если на граф G наложить отрезок a,x1 , то число рёбер увеличится на 2, а число областей не изменится (рис. 5.7).
При последовательном наложении отрезков x1,x2 ,..., xt-1, xt число рёбер увеличивается с каждым шагом на 2, а число областей на 1 (рис. 5.8). При добавлении же отрезка xt ,b число рёбер увеличивается
на 1, а число областей |
не изменяется |
(рис. 5.9), т.е. имеем |
||
n n t 2, |
h h 2t 1, |
t 1, |
n h n h . |
|
|
|
|
|
|
а |
xк |
xt-1 |
xt |
xk+1 |
|||
x1 |
|
|
|
Рис. 5.7 |
Рис. 5.8 |
|
Рис. 5.9 |
||
Способ 2. Пусть некоторые из точек |
x1,...,xt являются вершинами |
||||
графа G. И пусть число таких точек k k t . Тогда |
|||||
n n t k 2, |
h h 2t 1 k, |
t 1, |
n h n h |
|
|
Случай 3. Пусть точка а принадлежит графу G. Добавим к отрезку кусок так, чтобы он пересекался с G только в точке а (рис. 5.10). При этом эйлерова характеристика не изменилась и задача свелась к уже разобранному случаю. Остальные случаи очевидны.
53
Лемма 2. |
Пусть связный граф G получен наложением |
|
|
|
|
|
|
графа G1 |
на граф G. Тогда G G . |
|
|
|
|
|
|
|
a |
|
|||||
Доказательство. Проведём индукцию по числу рёбер h |
|
a |
|
|
|
||
|
|
|
|||||
графа G1. Лемма 1 даёт базис индукции. Предположим, что |
|
|
|
|
|
||
Рис. 5.10 |
|||||||
утверждение верно для графа G1 с числом рёбер h. Рас- |
|||||||
смотрим теперь граф сh + 1 ребром. |
|
|
|
|
|
||
Случай 1. В графе G1 найдутся два ребра, которые пересекаются с рёб-
рами графа G. Удаляя ребро графа G1, не являющееся перешейком, по-
лучим граф G с h рёбрами такой, что наложение G графа G на граф |
||
1 |
|
1 |
G связно. По индукционному предположению G G . Добавляя |
||
удалённое ребро по лемме 1, получим G G . |
||
Случай 2. Граф G1 |
пересекается с графом G по одному ребру . Если |
|
граф G1 не дерево, |
то в нём есть цикл. Удаляя ребро этого цикла, не |
|
совпадающее с и аналогично случаю 1, получим G G . Если |
||
же G1 – дерево, то в нем имеются по крайней мере два концевых ребра |
||
(тупика). Удаляя не совпадающий с |
тупик, с помощью тех же рас- |
|
суждений получим, что эйлеровы |
характеристики графов G и |
|
G1 совпадают. |
|
|
ТЕОРЕМА. Для любого плоского связного графа G имеем G 2 . Доказательство. Рассмотрим два плоских непересекающихся связных
графа G1 и G2. Пусть |
– дуга, одна вершина |
которой принадлежит G1, |
|
а другая G2. Пусть G – наложение на G . |
По лемме 2 G G , |
||
|
|
1 |
1 |
поскольку граф G |
связан. Кроме того, наложение G графа G на граф |
||
G2 также связно, |
а |
поэтому G G1 |
. Аналогично получим |
G G2 G1 G2 . Из произвольности графов и получаем, что
любые два плоских связных графа имеют одну и ту же эйлерову характеристику. Поэтому достаточно подсчитать её для простейшего плоского связного графа. Замечание. Условие связности графа существенно для доказательства
теоремы. Например, для несвязного графа G x1,x2 ,0 имеем
G 2 0 1 3.
5.8. Теорема Понтрягина – Куратовского
ТЕОРЕМА. Графы К3.3 и К5 не допускают плоской реализации. Доказательство. Предположим, что граф К3.3 имеет плоскую реализацию. Тогда для него 6 9 2 5.
54
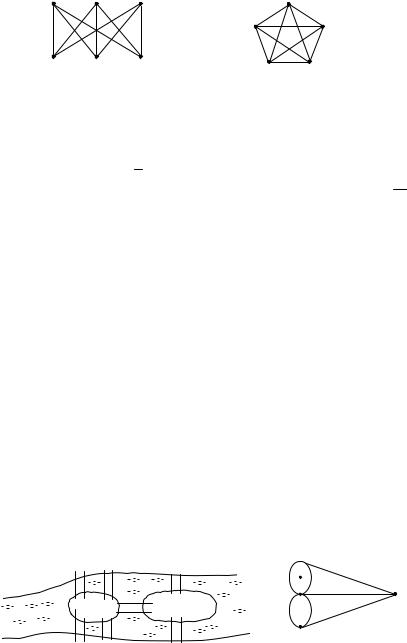
К3.3: |
x1 |
x2 |
x3 |
К5: |
|
y1 |
y2 |
y3 |
|
|
|
Рис. 5.11 |
|
Рис. 5.12 |
В графе К3.3 нет циклов длины 3, так как любое ребро ведёт из одной группы вершин к другой, т.е. любой цикл в G1 имеет длину 4.
Так как 5, то для числа рёбер графа имеем
h 1 5 hi 10 9 10 , 2i 1
где hi – число рёбер, ограничивающих грань с номером i 1,5, hi 4. Полученное противоречие доказывает первую часть теоремы.
Допустим, что граф К5 допускает плоскую реализацию. Для него
5 10 2 |
7. Пусть |
|
hi i |
|
имеют тот же смысл, что и |
|||
|
1,7 |
|||||||
раньше. Очевидно, |
|
1 |
7 |
|
3 7 |
|
Противоречие. |
|
h 3 h |
|
h |
|
|
10. |
|||
|
2 |
|||||||
|
i |
2i 1 i |
|
|
||||
Доказанная теорема допускает обращение.
ТЕОРЕМА Понтрягина – Куратовского. Для того, чтобы граф был пла-
нарным , чтобыон несодержал подграфов, гомеоморфныхК3.3 иК5.
Упражнения
1.Является ли планарным двудольный граф с двумя вершинами? Полный граф К6?
2.Является ли планарным граф
G1: 12 13 14 25 26 27 35 37 36 46 47 45 56 67; G2: 12 23 34 48 81 14 82 45 56 67 87 46;
G3: 12 13 15 18 23 24 34 38 45 46 47 56 57 58 67 78?
5.9. Эйлеровы графы
Задача о кенигсбергских мостах. Постановка и решение этой задачи Эйлером знаменует начало разработки теории графов. Расположение мостов через реку Прегель в г. Кенигсберге в его время
приведено на рис. 5.13. |
|
|
С |
|
||
|
|
|
|
с |
C |
g |
C |
с |
d |
g |
A |
d e |
D |
|
A |
e |
D |
a |
b |
f |
|
a |
b |
f |
|
|
|
B |
|
B |
|
|||
|
|
|
|
|
||
|
|
Рис. 5.13 |
|
|
Рис. 5.14 |
|
Требуется пройти каждый мост по одному разу и вернуться в исходную часть города. Можно построить граф задачи, в которой каждой части города соответствует вершина, а каждому мосту – ребро, инцидентное вершинам, относящимся к соединяемым им частям (рис. 5.14). Обходу мостов соответствует маршрут графа, который по условию должен быть простым циклом. Эйлеровой цепью графа называется маршрут, включающий все рёбра графа и через каждое ребро проходящей по одному разу. Замкнутая эйлерова цепь – эйлеров цикл. Эйлерову цепь и эйлеров цикл называют эйлеровыми графами.
ТЕОРЕМА. Граф имеет эйлеров цикл а) связен, б) все его вершины имеют положительные чётные степени.
Доказательство. Необходимость очевидна.
Докажем вначале, что в графе G V, X , все вершины которого
имеют чётную степень, для любого ребра x найдётся цикл, содержащий x. Пусть a0, a1 – концы ребра x. Так как степень вершины a1 чётна, то найдётся другое ребро x2, отличное от x, инцидентное a1. Пусть a2 –
вторая концевая точка ребра x2. Маршрут a0,x1 ,a1,x2,a2 простой. Про-
должая таким образом a0,x1 ,a1,x2,a2,x3,..., получим последователь-
ность простых маршрутов увеличивающейся длины. В силу конечности графа через некоторое время продлить маршрут будет невозможно. Это значит, чтомаршрут заканчивается в вершине a0.
Рассмотрим в графе G замкнутый простой маршрут a0,x1,...,a a0 , содержащий наибольшее число рёбер. Покажем, что в
графе нет вершин, не лежащих на этом маршруте. Предположим, что некоторая вершина b не лежит на нём. Так как граф связан, то существуют цепи между b и каждой из всех вершин a0,...,a 1 максимального
маршрута. Рассмотрим самую короткую цепь b b0, y1, b1,...,ym,bm ai.
Вершины b0,...,bm 1 не могут совпадать с вершинами a0,...,a 1 , в про-
тивном случае можно было бы выбрать цепь длины m. Следовательно, реброym не входит в выбранный путь.
Из множества рёбер графа удалим x1,...,x и полученное множе-
ство рёбер обозначим через X . В графе V, X все вершины имеют чётную степень, т.е. в нём существует простой замкнутый маршрут, включающий ребро ym. Пусть это будет маршрут ai, ym,...,ai .
Если в исходный маршрут вместо ai подставить этот маршрут, то получим маршрут длины . Это противоречит тому, что – максимальная длина простого замкнутого маршрута в графе. Итак, простой замкнутый маршрут максимальной длины проходит через все вершины графа.
55 |
56 |

Предположим, что он содержит не все рёбра графа. Тогда в графе найдётся ребро y, инцидентное одной из вершин ai и не входящее в максимальный маршрут. Повторив рассуждения, проведённые для ym, получим противоречие.
Следствие. Граф имеет открытую эйлерову цепь а) связен, б) содержит ровно две вершины нечётной степени.
Необходимость очевидна.
Пусть a, b – две вершины нечётной степени. Соединим их ещё одним ребром x. После этого все вершины графа приобретут чётную степень, т.е. в нём существует замкнутая эйлерова цепь. Осталось удалить из неё ребро x.
Гамильтоновой цепью графа называется цепь, которая проходит через все вершины графа и через каждую проходит по одному разу. Гамильтоновым циклом называется замкнутая гамильтонова цепь.
ТЕОРЕМА. Если число вершин графа n > 3 и степени всех вершин больше, чем n/2, то граф гамильтонов.
Упражнения
1.Приведите примеры эйлерова, но не гамильтонова графа; неэйлерова, но гамильтонова графа; неэйлерова и одновременно негамильтонова графа.
2.Существуют ли эйлеровы циклы или гамильтоновы цепи для следующих графов:
(1) |
(2) |
5.10. Оценка числа графов
Лемма 1. |
|
|
n |
n |
|
|
|
|
|
|
|
|
|
|
|||||
n! |
|
|
|
; (e 2,718281828 , число Непера). |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
||||
Доказательство. |
Проведём индукцию по n. При n 1 |
имеем 1 |
1 |
. |
|||||||||||||||
e |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
k k |
|
|
k |
k |
e kk |
|
|
k 1 k 1 |
|
|
|||||||
Пусть |
k! |
|
. |
Тогда (k |
+ 1)! |
|
k 1 |
|
k |
1 |
|
|
|
, |
|||||
|
|
e |
|
|
e |
ek 1 |
|
|
ek 1 |
|
|
||||||||
так как |
e kk k 1 k , что в свою очередь следует из известного нера- |
|||||
|
|
1 |
k |
|
k 1 k |
|
венства |
e 1 |
|
|
|
|
.■ |
|
kk |
|||||
|
|
k |
|
|
||
|
|
|
|
|
|
57 |
Лемма 2. Cnk nk . k!
Доказательство. Сnk n n 1.... n k 1 nk .■ k! k!
ТЕОРЕМА. Пусть h – число всех попарно неизоморфных графов с
h рёбрами без изолированных вершин. Тогда h e 2eh h .
Доказательство. Граф с h рёбрами имеет не более 2h вершин. Занумеруем вершины графа числами 1, 2, …. Число пар вершин, которые могут связываться рёбрами, не превосходит величины
|
|
|
|
|
|
|
k С22h n C22h 1 h 2h 1 . |
|
|
|
Crh n |
||||||||
|
|
Из r рёбер графа с h рёбрами можно построить не более |
|||||||||||||||||
графов, т.е. |
|
|
r h 1h |
2h2 2h 1h |
|
2h2 2hh |
|
2h2 h |
|
|
|
|
|||||||
|
|
h |
|
|
h |
|
|
|
|
1 |
h |
||||||||
h Cr |
n Cr h 1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||
|
|
h! |
|
h! |
h! |
|
|||||||||||||
|
|
|
|
|
|
|
|
h! |
|
|
|
|
|
h |
|||||
|
2 |
h |
e |
h |
|
h |
|
|
|
|
|
|
|
|
|
|
|||
2h |
|
|
|
2eh |
e.■ |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
h |
|
|
|
Упражнение |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Докажите, что |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1) |
число всех различных попарно неизоморфных графов с n пере- |
||||||||||||||||||
нумерованными вершинами равно 2Сn2 |
; |
|
|
|
|
|
|
|
|
||||||||||
2) |
число всех различных попарно неизоморфных графов с n пере- |
||||||||||||||||||
нумерованными |
вершинами |
без |
изолированных |
вершин |
равно |
||||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 k Cnk 2Cn2 k . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
k 0 |
|
Указание. В задаче 2) воспользоваться принципом включения |
|||||||||||||||||
|
|
||||||||||||||||||
и исключения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5.11. Деревья |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Граф без циклов называется лесом. Связный граф, не содержа- |
|||||||||||||||||
щий простых циклов, называется деревом. |
|
|
|
|
|
|
|
|
|||||||||||
ТЕОРЕМА. Граф является деревом любые две его различные вершины соединяет единственная цепь.
Доказательство очевидно.
ТЕОРЕМА. Связный граф является деревом число вершин в нём на единицу больше числа рёбер.
Доказательство. Пусть граф является деревом. Проведём индукцию по числу рёбер h. Если h = 1, то граф является деревом и у него
58
число вершин на 1 превосходит число рёбер. Пусть для дерева с h = k рёбрами утверждение верно. Дерево, содержащее две или более вершин, имеет по крайней мере две концевые вершины. В самом деле, ими являются вершины маршрута максимальной длины в графе. После удаления из дерева одной из его концевых вершин вместе с инцидентным ей ребром вновь получается дерево. Рассмотрим дерево с k + 1 ребром. Удаление концевого ребра даёт нам дерево, удовлетворяющее гипотезе индукции. Так как удаление концевого ребра происходит с одновременным удалением и вершины, то в графе с k + 1 ребром наблюдается то же соотношение между числом рёбер и числом вершин, что и в графе с
kрёбрами.
Пусть в связном графе n вершин и h рёбер, причём n = h + 1. Если в графе есть циклы, то из каждого цикла удаляем по одному ребру. В результате получим остовное дерево, в котором число вершин n, а
рёбер h s , где s – число удалённых рёбер. Из необходимой части теоремы n h s 1 s 0 , т.е. исходный граф не имеет циклов.
Число s h n 1 называется цикломатическим числом связного графа с n вершинами и h рёбрами.
Следствие. Связный граф является деревом его цикломатическое число равно нулю.
Упражнение
Перечислить все восьмивершинные деревья (23).
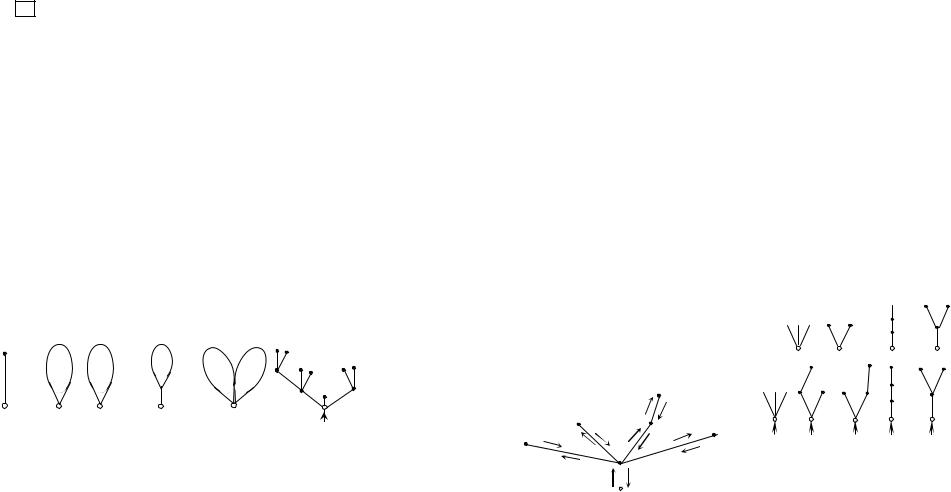
5.12. Корневое дерево
Граф с выделенными вершинами называется сетью. Выделенные вершины называются полюсами сети. Примером однополюсной сети является корневое дерево. Дерево с выделенной вершиной называется корневым деревом, а выделенная вершина называется корнем. Все вершины корневого дерева в зависимости от расстояния от корня обычно располагают поярусам. Приведём индуктивное определениекорневогодерева.
Базис индукции. Фигура рис. 5.15 является корневым деревом с корнем а.
Индуктивный переход. Тогда фигура С, полученная подключением к корню нового ребра (рис. 5.17а), тоже дерево. Фигура D, полученная из A и B отождествлением их корней, – тоже дерево (рис. 5.17б). Других деревьев нет.
Плоскую геометрическую реализацию дерева, в которой рёбра представляют отрезки прямых, а корень изображён вершиной со стрелкой, будем называть укладкой дерева. Стрелка указывает на то, что плоское корневое дерево изображается на плоскости с разрезом, представляющим собой полупрямую, исходящую из корня. Тем самым можно считать заданным направление подсчёта рёбер в ярусах слева направо.
Каждому плоскому корневому дереву с h рёбрами можно однозначно сопоставить двоичный вектор длины 2h, называемый кодом дерева. Дереву с одним ребром сопоставим вектор 01. Если деревьям A и B (рис. 5.16) сопоставлены коды и , то дереву С, полученному
подключением ребра, – код 0 1, дереву D, полученному отождествлением корней, – код .
Каждой укладке дерева соответствует вектор-кортеж, содержащий поровну нулей и единиц, причём в любом его начальном отрезке нулей не меньше, чем единиц. Если в каком-либо собственном начальном отрезке кортежа нулей и единиц поровну, то это означает, что кортеж соответствует укладке дерева D, полученного из деревьев A и B отождествлением корней. Отсюда видно, что в силу индуктивности определения деревьев и кодов по своему кортежу укладка дерева восстанавливается однозначно, т.е. имеем взаимнооднозначное соответствие между укладками деревьев с h рёбрами и подмножеством множества кортежей длины 2h, содержащих поровну нулей и единиц. Обозначим
через h число всех попарно неизоморфных деревьев с h рёбрами, а
через * h число всех различных укладок деревьев с h рёбрами. Пример. Все корневые деревья с тремя ребрами: 

a1 |
|
|
|
|
|
|
|
Д |
А |
|
9 |
10 |
|
|
|
ярус 3 |
Все укладки с тремя ребрами: |
А |
|
|
B |
C |
|
D |
B |
|
|
|
|
||||||
|
|
|
|
A |
|
|
5 |
6 |
7 |
8 |
ярус 2 |
|
|||||
|
|
|
|
|
|
b |
|
|
|
|
|
|
|||||
a |
a) |
a |
б) |
b |
a) |
|
б) |
a=b |
|
4 |
2 |
|
|
|
|
||
a |
|
|
1 |
3 |
|
ярус 1 |
1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
Рис. 5.15 |
Рис. 5.16 |
Рис. 5.17 |
Рис. 5.18 |
1 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
1 |
|
Задача. |
По |
заданному |
коду |
|
|
|
|
|
0 |
|
1 |
|||||
Гипотеза индукции. Пусть |
A – дерево с корнем а, В – дерево с |
0 |
|
|
001010011011 |
построить |
плоское |
||||
|
|
|
|||||||||
|
|
|
|||||||||
корнем b (рис. 5.16). |
|
|
|
0 |
1 |
|
корневое дерево. |
|
|
||
59 |
60 |
Рис. 5.19 |
|
