
- •Логика предикатов
- •§ 1. Основные понятия
- •§ 2. Классификация предикатов
- •Примеры:
- •§ 3. Множество истинности предиката
- •Примеры:
- •Утверждения:
- •Примеры:
- •§ 4. Равносильность предикатов
- •Пример 1
- •§ 5. Логические операции над предикатами Отрицание предиката
- •Примеры:
- •Пример 3
- •Предикат от n переменных и квантор общности
- •Квантор существования
- •Замечание
- •Предикат от n переменных и квантор существования
- •Замечание
- •Примечание
- •§ 7. Численные кванторы
- •Ограниченные кванторы
- •§ 8. Формулы логики предикатов
- •Определение формулы логики предикатов (по индукции)
- •§ 9. Классификация формул логики предикатов
- •Классификационные определения для формул логики предикатов
- •Значение формулы логики предикатов
- •§ 10. Тавтологии (равносильности) логики предикатов
- •Доказательство
- •§ 11. Равносильные преобразования формул
- •Пример неравносильных формул
- •§ 12. Общезначимость и выполнимость
- •Из определений следует:
- •Связь между общезначимостью и выполнимостью формул логики предикатов.
- •Проблема разрешения для общезначимости и выполнимости формул.
- •Решение проблемы для формул на конечных множествах.
- •Алгоритм распознавания общезначимости формул в частных случаях
- •Теорема 1
- •Следствие
- •Решение проблемы для -формул и-формул.
- •§ 13. Примеры и задачи
- •§ 14. Решение примеров
- •Решение
- •Решение
- •Решение
- •Решение примеров:
- •Литература
- •Содержание
Квантор существования
Определение.
Операцией
связывания квантором существования
называется правило, по которому любому
одноместному предикату P(x),
определенному на множестве M,
сопоставляется высказывание, обозначаемое
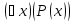 ,
которое ложно в том и только том случае,
когдаP(x) –
тождественно ложен и истинно в противном
случае:
,
которое ложно в том и только том случае,
когдаP(x) –
тождественно ложен и истинно в противном
случае:
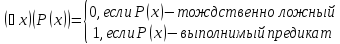
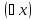 -
квантор существования по переменной
-
квантор существования по переменной
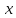
Пример
Имеем
два одноместных предиката определенных
на множестве N:
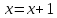 и
и 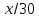
Первый
предикат – тождественно ложный,
следовательно 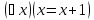 –ложное
высказывание.
–ложное
высказывание.
Второй
предикат – выполнимый, следовательно
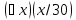 – истинное высказывание.
– истинное высказывание.
Замечание
Если
одноместный предикат P(x)
задан на конечном множестве
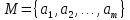 то высказывание
то высказывание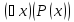 эквивалентно дизъюнкции
эквивалентно дизъюнкции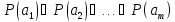 .
.
Действительно,
по определению 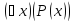 – высказывание имеет значение 0 (т.е.
ложно), еслиP(x)
– тождественно ложный предикат, т.е.
любое из высказываний
– высказывание имеет значение 0 (т.е.
ложно), еслиP(x)
– тождественно ложный предикат, т.е.
любое из высказываний
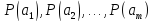 ,
в которое может превратиться предикат,
ложно. А это означает ложность дизъюнкции
,
в которое может превратиться предикат,
ложно. А это означает ложность дизъюнкции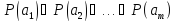 .
.
В
выражении
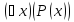 ,
так же как и в
,
так же как и в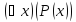 ,
переменнаяx
перестает быть переменной в обычном
смысле слова: это – связанная
переменная.
,
переменнаяx
перестает быть переменной в обычном
смысле слова: это – связанная
переменная.
Предикат от n переменных и квантор существования
Определение.
Операцией
связывания квантором существования по
переменной
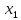 называется правило, по которому каждому
n-местному
предикату (n≥2)
называется правило, по которому каждому
n-местному
предикату (n≥2)
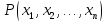 ,
определенному на множествах
,
определенному на множествах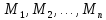 ,
сопоставляется новый (n-1)-местный
предикат, обозначаемый
,
сопоставляется новый (n-1)-местный
предикат, обозначаемый
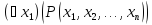 ,
который для любых предметов
,
который для любых предметов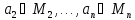 ,
превращается в высказывание
,
превращается в высказывание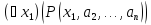 ,
ложное тогда и только тогда, когда
одноместный предикат
,
ложное тогда и только тогда, когда
одноместный предикат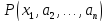 ,
определенный на множестве
,
определенный на множестве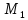 тождественно ложен и истинен в
противоположном случае, то есть:
тождественно ложен и истинен в
противоположном случае, то есть:
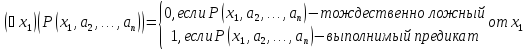
Пример
1. Двухместный
предикат
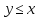 ,
определенный наR.
Применим к нему квантор существования
по переменной x.
,
определенный наR.
Применим к нему квантор существования
по переменной x.
Получим
одноместный предикат
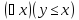 ,
зависящий от переменной y. Этот предикат
превращается в истинное высказывание,
если вместо него подставить конкретное
число
,
зависящий от переменной y. Этот предикат
превращается в истинное высказывание,
если вместо него подставить конкретное
число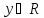 ,
т.е. является тождественно истинным
предикатом.
,
т.е. является тождественно истинным
предикатом.
Пример
2. Двухместный
предикат
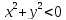 ,
определенный наR.
Применение квантора существования по
любой переменной даст одноместный
предикат, который будет тождественно
ложным:
,
определенный наR.
Применение квантора существования по
любой переменной даст одноместный
предикат, который будет тождественно
ложным:
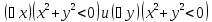
Замечание
К
(n-1)-местному
предикату
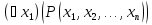 ,
, можно снова применить квантор общности
или квантор существования. Получим
(n-2)-местные
предикаты:
,
, можно снова применить квантор общности
или квантор существования. Получим
(n-2)-местные
предикаты:
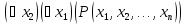
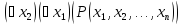
Пример.
На
множестве M
задан двухместный предикат P(x,
y).
Применение к нему кванторной операции
по переменной x
ставит в соответствие двухместному
предикату P(x,
y)
одноместные предикаты
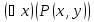 или
или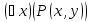 ,
зависящие от переменнойy.
,
зависящие от переменнойy.
К этим предикатам опять применяем кванторные операции по переменной y, которые приведут к нульместному предикату (высказыванию) следующих видов:
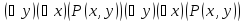
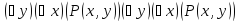
Например,
предикат
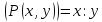 ,
определенный на множествеN.
,
определенный на множествеN.
Применение кванторных операций к предикату P(x, y) приводит к 8 возможным высказываниям:
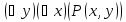 –«Для
всякого y
и для всякого x,
y
является делителем x»
(ложное высказывание)
–«Для
всякого y
и для всякого x,
y
является делителем x»
(ложное высказывание)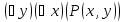 –«Существует
y
такое, которое является делителем
всякого x»
(истинное высказывание)
–«Существует
y
такое, которое является делителем
всякого x»
(истинное высказывание)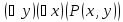 –«Для
всякого y
существует x
такое, что x
делится на y»
(истинное высказывание)
–«Для
всякого y
существует x
такое, что x
делится на y»
(истинное высказывание)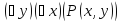 –«Существует
y
и существует x,
такие что y
является делителем x»
(истинное высказывание)
–«Существует
y
и существует x,
такие что y
является делителем x»
(истинное высказывание) 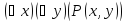 –«Для
всякого x
и для всякого y
y является
делителем x»
(ложное высказывание)
–«Для
всякого x
и для всякого y
y является
делителем x»
(ложное высказывание) 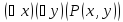 –«Для
всякого x
существует y
такое, что x
делится на y»
(истинное высказывание)
–«Для
всякого x
существует y
такое, что x
делится на y»
(истинное высказывание) 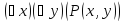 –«Существует
x
такое, что для всякого y,
x
делится на y»
(ложное)
–«Существует
x
такое, что для всякого y,
x
делится на y»
(ложное)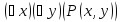 –«Существует
x
и y
такие, что y
является делителем x»
(истинное высказывание)
–«Существует
x
и y
такие, что y
является делителем x»
(истинное высказывание)
В общем случае изменение порядка следования кванторов изменяет смысл высказывания, а значит и его логическое значение (примеры 3 и 7).
