
- •Логика предикатов
- •§ 1. Основные понятия
- •§ 2. Классификация предикатов
- •Примеры:
- •§ 3. Множество истинности предиката
- •Примеры:
- •Утверждения:
- •Примеры:
- •§ 4. Равносильность предикатов
- •Пример 1
- •§ 5. Логические операции над предикатами Отрицание предиката
- •Примеры:
- •Пример 3
- •Предикат от n переменных и квантор общности
- •Квантор существования
- •Замечание
- •Предикат от n переменных и квантор существования
- •Замечание
- •Примечание
- •§ 7. Численные кванторы
- •Ограниченные кванторы
- •§ 8. Формулы логики предикатов
- •Определение формулы логики предикатов (по индукции)
- •§ 9. Классификация формул логики предикатов
- •Классификационные определения для формул логики предикатов
- •Значение формулы логики предикатов
- •§ 10. Тавтологии (равносильности) логики предикатов
- •Доказательство
- •§ 11. Равносильные преобразования формул
- •Пример неравносильных формул
- •§ 12. Общезначимость и выполнимость
- •Из определений следует:
- •Связь между общезначимостью и выполнимостью формул логики предикатов.
- •Проблема разрешения для общезначимости и выполнимости формул.
- •Решение проблемы для формул на конечных множествах.
- •Алгоритм распознавания общезначимости формул в частных случаях
- •Теорема 1
- •Следствие
- •Решение проблемы для -формул и-формул.
- •§ 13. Примеры и задачи
- •§ 14. Решение примеров
- •Решение
- •Решение
- •Решение
- •Решение примеров:
- •Литература
- •Содержание
Пример 3
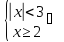
множество
истинности предиката
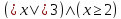 ,
определенного наR:
,
определенного наR:
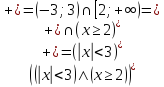 .
.
Пример 4
P(x) = «x – четное число»,
Q(x) = «x – кратно 3»,
P( )&Q(
)&Q(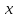 )
= «x
– четное число и x
кратно 3» = «x
делится на 6».
)
= «x
– четное число и x
кратно 3» = «x
делится на 6».
Дизъюнкция двух предикатов
Определение.
Дизъюнкцией
двух
предикатов P(x) и
Q(x)
называется новый предикат
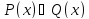 ,
который принимает значение «ложь» при
таких и только таких значениях
,
который принимает значение «ложь» при
таких и только таких значениях ,
при которых каждый из предикатов
принимает значение «ложь» и принимает
значение «истина» во всех остальных
случаях.
,
при которых каждый из предикатов
принимает значение «ложь» и принимает
значение «истина» во всех остальных
случаях.
Пример 5
Даны
два одноместных предиката
 , определенные
на R.
Дизъюнкция двух одноместных предикатов:
, определенные
на R.
Дизъюнкция двух одноместных предикатов:
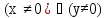 – двухместный предикат, равносилен
предикату
– двухместный предикат, равносилен
предикату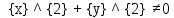 наR.
наR.
Теорема
Для
n-местных
предикатов
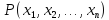 и
и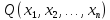 ,
определенных на множествах
,
определенных на множествах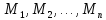 ,
множество истинности дизъюнкции
,
множество истинности дизъюнкции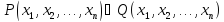 совпадает с объединением множеств
истинности исходных предикатов:
совпадает с объединением множеств
истинности исходных предикатов:
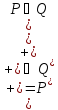
Следствие
Дизъюнкция двух предикатов есть выполнимый предикат тогда и только тогда, когда по меньшей мере один из данных предикатов выполним.
Следствие
Дизъюнкция двух предикатов тождественно истинна тогда и только тогда, когда оба данных предиката тождественно истинны.
Примеры:
Найти множество истинности предиката
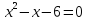 ,
определенного наR.
,
определенного наR.
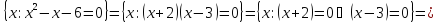
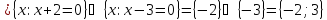
Дизъюнкция двух двухместных предикатов, определенных на R:
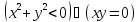 есть
выполнимый предикат, т.е. выполним один
из них: xy=0.
есть
выполнимый предикат, т.е. выполним один
из них: xy=0.
Импликация двух предикатов
Определение.
Импликацией
предикатов
P(x)
и Q(x)
называется новый предикат
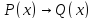 ,
который является ложным при тех и только
тех значениях
,
который является ложным при тех и только
тех значениях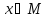 ,
при которых одновременноP(x)
принимает значение «истина», а Q(x)
– значение «ложь» и принимает значение
«истина» во всех остальных случаях.
,
при которых одновременноP(x)
принимает значение «истина», а Q(x)
– значение «ложь» и принимает значение
«истина» во всех остальных случаях.
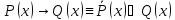
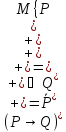
§ 6. Кванторные операции над предикатами
Квантор общности.
Определение.
Операцией
связывания квантором общности
называется правило, по которому каждому
одноместному предикату P(x),
определенному на множестве M,
сопоставляется высказывание, обозначаемое
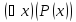 ,
(читается: для всякого значенияx
P(x)
истинное высказывание), которое истинно
в том и только том случае, когда предикат
P(x)
тождественно истинен и ложно в
противоположном случае:
,
(читается: для всякого значенияx
P(x)
истинное высказывание), которое истинно
в том и только том случае, когда предикат
P(x)
тождественно истинен и ложно в
противоположном случае:
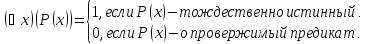
Символ
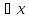 – квантор общности по переменнойx.
– квантор общности по переменнойx.
Примеры:
Рассмотрим
одноместные предикаты на множестве N:
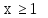 и
и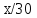 .
.
Первый
предикат – тождественно истинный,
следовательно
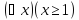 - истинное высказывание.
- истинное высказывание.
Второй
предикат – опровержимый, следовательно
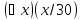 – ложное высказывание.
– ложное высказывание.
В
выражении
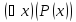 вместоx
нельзя ничего подставлять. Говорят, что
переменная x
– связанная.
вместоx
нельзя ничего подставлять. Говорят, что
переменная x
– связанная.
В математике переменные могут быть связаны не только квантором.
Связанные переменные в следующих выражениях:
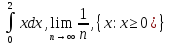
Любое из этих выражений не зависит от связанных переменных.
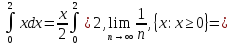
Замечание.
Если
одноместный предикат P(x)
задан на конечном множестве
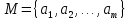 ,тогда
высказывание
,тогда
высказывание
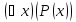 эквивалентно
конъюнкции
эквивалентно
конъюнкции
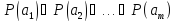 .
.
Предикат от n переменных и квантор общности
Определение.
Операцией
связывания квантором общности по
переменной
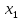 называется правило, по которому любому
n-местному
предикату
называется правило, по которому любому
n-местному
предикату
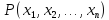 ,
определенному на множествах
,
определенному на множествах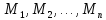 ,
сопоставляется новый (n-1)-местный
предикат, обозначаемый
,
сопоставляется новый (n-1)-местный
предикат, обозначаемый
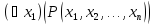 ,
который для любых предметов
,
который для любых предметов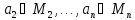 ,
превращается в высказывание
,
превращается в высказывание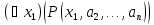 ,
истинное в том и только том случае, когда
одноместный предикат
,
истинное в том и только том случае, когда
одноместный предикат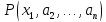 ,
определенный на множестве
,
определенный на множестве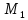 тождественно истинен и ложное в
противоположном случае, то есть:
тождественно истинен и ложное в
противоположном случае, то есть:

Пример.
Рассмотрим
двухместный предикат
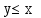 ,
определенный на множествеN.
Применим к нему квантор общности по
переменной x.
Получим одноместный предикат
,
определенный на множествеN.
Применим к нему квантор общности по
переменной x.
Получим одноместный предикат
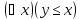 ,
зависящий от переменнойy.
Этот предикат может превратиться в
истинное высказывание при y=1
и в ложное – при y
≠ 1.
,
зависящий от переменнойy.
Этот предикат может превратиться в
истинное высказывание при y=1
и в ложное – при y
≠ 1.
Замечание.
К
(n-1)-местному
предикату
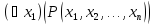 ,
зависящему от переменных
,
зависящему от переменных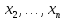 ,
можно снова применить операцию связывания
квантором общности по любой свободной
переменной. В результате получится
(n-2)-местный
предикат.
,
можно снова применить операцию связывания
квантором общности по любой свободной
переменной. В результате получится
(n-2)-местный
предикат.
Например,
применим к одноместному предикату
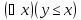 квантор общности по переменнойy
и получим нульместный предикат, т.е.
высказывание:
квантор общности по переменнойy
и получим нульместный предикат, т.е.
высказывание:
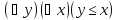 .
Полученное высказывание ложно, т.к.
.
Полученное высказывание ложно, т.к.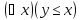 опровержимый предикат от переменнойy.
опровержимый предикат от переменнойy.
Замечание. Любое высказывание можно рассматривать как предикат, содержащий нуль предметных переменных, т.е. как нульместный предикат.
