
- •Логика предикатов
- •§ 1. Основные понятия
- •§ 2. Классификация предикатов
- •Примеры:
- •§ 3. Множество истинности предиката
- •Примеры:
- •Утверждения:
- •Примеры:
- •§ 4. Равносильность предикатов
- •Пример 1
- •§ 5. Логические операции над предикатами Отрицание предиката
- •Примеры:
- •Пример 3
- •Предикат от n переменных и квантор общности
- •Квантор существования
- •Замечание
- •Предикат от n переменных и квантор существования
- •Замечание
- •Примечание
- •§ 7. Численные кванторы
- •Ограниченные кванторы
- •§ 8. Формулы логики предикатов
- •Определение формулы логики предикатов (по индукции)
- •§ 9. Классификация формул логики предикатов
- •Классификационные определения для формул логики предикатов
- •Значение формулы логики предикатов
- •§ 10. Тавтологии (равносильности) логики предикатов
- •Доказательство
- •§ 11. Равносильные преобразования формул
- •Пример неравносильных формул
- •§ 12. Общезначимость и выполнимость
- •Из определений следует:
- •Связь между общезначимостью и выполнимостью формул логики предикатов.
- •Проблема разрешения для общезначимости и выполнимости формул.
- •Решение проблемы для формул на конечных множествах.
- •Алгоритм распознавания общезначимости формул в частных случаях
- •Теорема 1
- •Следствие
- •Решение проблемы для -формул и-формул.
- •§ 13. Примеры и задачи
- •§ 14. Решение примеров
- •Решение
- •Решение
- •Решение
- •Решение примеров:
- •Литература
- •Содержание
Министерство образования и науки Российской Федерации
Дальневосточный федеральный университет
Школа естественных наук
И. А. Курочкина
Логика предикатов
Учебное пособие
Владивосток
Издательский дом Дальневосточного федерального университета
2013
УДК 510.6
ББК 22.12
К 93
Курочкина, И. А.
К93 Логика предикатов: учебное пособие / И. А. Курочкина. – Владивосток : Издательский дом Дальневосточного федерального университета, 2013. – 44 с.
Пособие является третьей частью курса лекций по математической логике и теории алгоритмов. Включает изложение теоретического материала по логике предикатов, примеры решений задач, упражнения и варианты контрольных работ.
Для студентов, обучающихся по образовательным программам бакалавриата и магистратуры «Прикладная информатика».
УДК 510.6
ББК 22.12
© Курочкина И.А., 2013
§ 1. Основные понятия
Определение.
n‑местным
предикатом, определенном на множествах
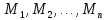 называется предложение, содержащееn
переменных
называется предложение, содержащееn
переменных
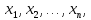 превращающееся в высказывание при
подстановке вместо этих переменных
любых конкретных элементов из множеств
превращающееся в высказывание при
подстановке вместо этих переменных
любых конкретных элементов из множеств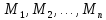 соответственно.
соответственно.
Для
n-местного
предиката будем использовать обозначение
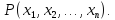
Переменные
 называютпредметными.
называютпредметными.
Элементы
множеств
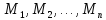 ,
которые эти элементы пробегают –конкретные
предметы:
,
которые эти элементы пробегают –конкретные
предметы:
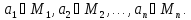
Итак,
предикат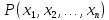 ,
определенный на множествах
,
определенный на множествах
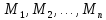 ,
превращается в конкретное высказывание
,
превращается в конкретное высказывание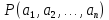 ,
если вместо предметных переменных
,
если вместо предметных переменных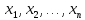 подставить
в него конкретные предметы: элементы
подставить
в него конкретные предметы: элементы
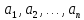 из
множеств
из
множеств
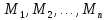 соответственно.
соответственно.
Это высказывание может быть либо истинным, либо ложным, то есть его логическое значение равно 1 или 0.
Следовательно,
данный предикат определяет функцию
n-аргументов,
заданную на множествах
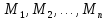 и
принимающий значение в двухэлементном
множестве {0,1}. Эту функцию и называютпредикатом.
и
принимающий значение в двухэлементном
множестве {0,1}. Эту функцию и называютпредикатом.
§ 2. Классификация предикатов
Определение.
Предикат
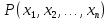 ,
заданный на множествах
,
заданный на множествах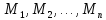 называется:
называется:
Тождественно-истинным, если при любой подстановке вместо переменных
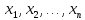 любых
конкретных предметов
любых
конкретных предметов
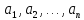 из
множеств
из
множеств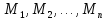 соответственно он превращается в
истинное высказывание
соответственно он превращается в
истинное высказывание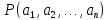 ;
;Тождественно-ложным, если при любой подстановке вместо переменных
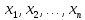 ,
любых конкретных предметов
,
любых конкретных предметов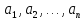 из множеств
из множеств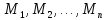 соответственно он превращается в ложное
высказывание;
соответственно он превращается в ложное
высказывание;Выполнимым (опровержимым), если существует по крайней мере один набор конкретных предметов
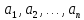 из множеств
из множеств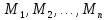 соответственно,
при подстановке которого вместо
соответствующих предметных переменных
в предикат
соответственно,
при подстановке которого вместо
соответствующих предметных переменных
в предикат
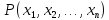 он превращается в истинное (ложное)
высказывание
он превращается в истинное (ложное)
высказывание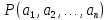 .
.
Примеры:
Одноместный предикат «Город x расположен на берегу реки Волги».
Определен на множестве названий городов, является выполнимым.
Одноместный предикат «
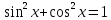 »
определен на множестве R,
тождественно истинный.
»
определен на множестве R,
тождественно истинный.Двухместный предикат «
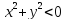 »
задан на множествеR,
тождественно ложный.
»
задан на множествеR,
тождественно ложный.
Утверждения:
Любой тождественно-истинный предикат является выполнимым, обратное неверно.
Любой тождественно-ложный является опровержимым, обратное неверно.
Любой не тождественно-истинный предикат будет опровержимым.
Любой не тождественно-ложный предикат будет выполнимым.
§ 3. Множество истинности предиката
Определение.
Множеством
истинности
предиката
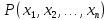 ,
заданного на множествах
,
заданного на множествах
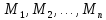 называется
совокупность всех упорядоченныхn-систем
(n-арок)
называется
совокупность всех упорядоченныхn-систем
(n-арок)
 ,>
в которых
,>
в которых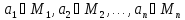 ,
таких, что данный предикат обращается
в истинное высказывание
,
таких, что данный предикат обращается
в истинное высказывание
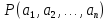 при подстановке
при подстановке
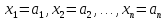 .
Это множество будем обозначатьP+.
.
Это множество будем обозначатьP+.
Таким
образом, P+
= {<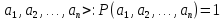 }
}
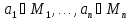
Множество
истинности n-местного предиката
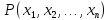
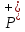 представляет собойn-арное
отношение между элементами множеств
представляет собойn-арное
отношение между элементами множеств
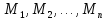 .
.
Пусть
P(x) –
одноместный предикат, M –
область определения предиката P(x).
множество истинности предиката
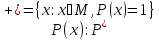
То
есть
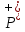 является подмножеством множества M:
является подмножеством множества M:
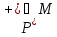 .
.
