
ЛабРаб-6
.doc1. Эрмитовы кубические сплайны
Пусть на сетке
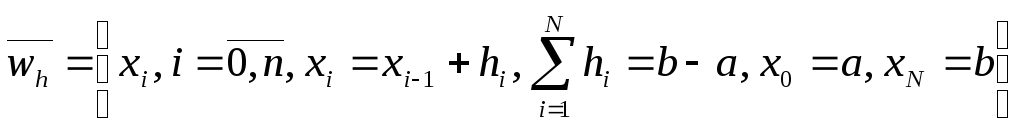 заданы значения
заданы значения
![]() .
.
Определение. Эрмитовым кубическим
сплайном называют функцию
![]() ,
удовлетворяющую условиям:
,
удовлетворяющую условиям:
-
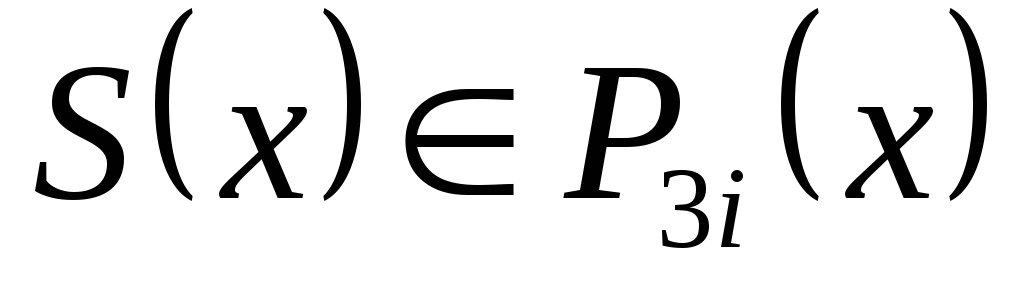 ,
для
,
для
 ,
, -
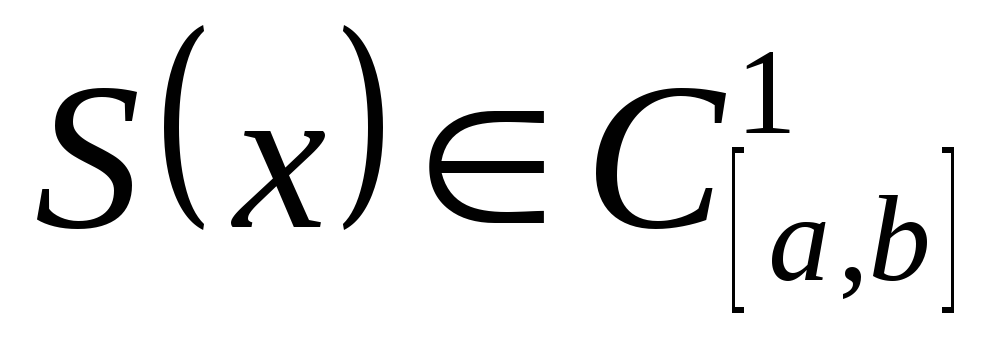 ,
(т.е. непрерывны
,
(т.е. непрерывны
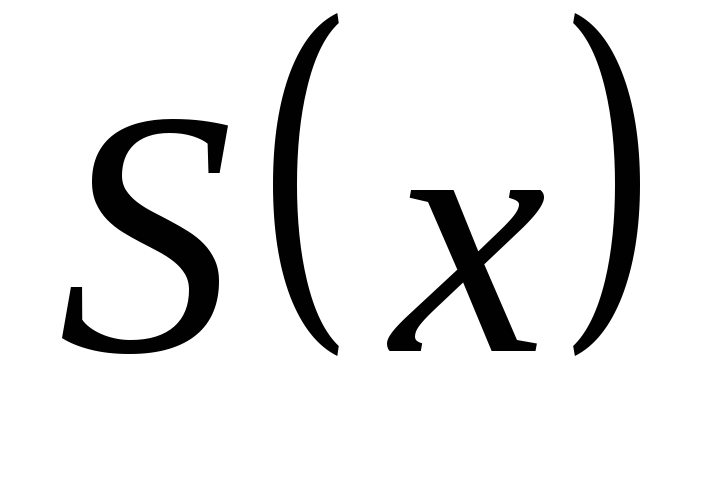 и
и
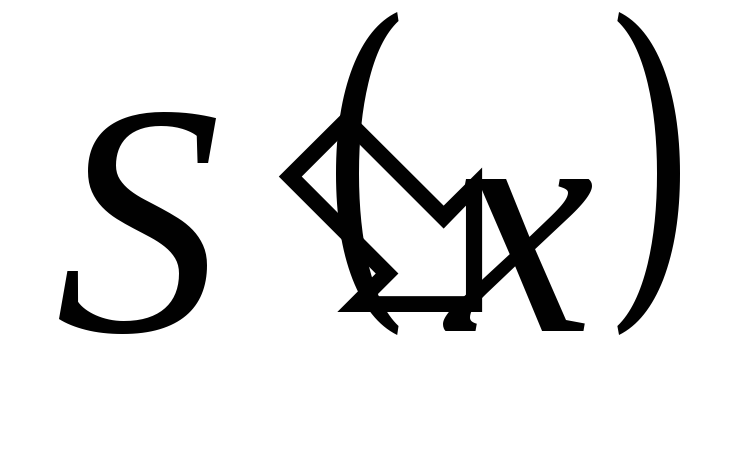 во внутренних узлах),
во внутренних узлах), -
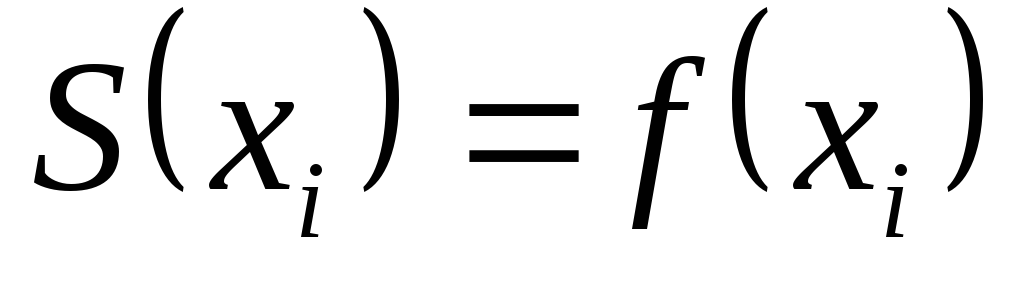 ,
,
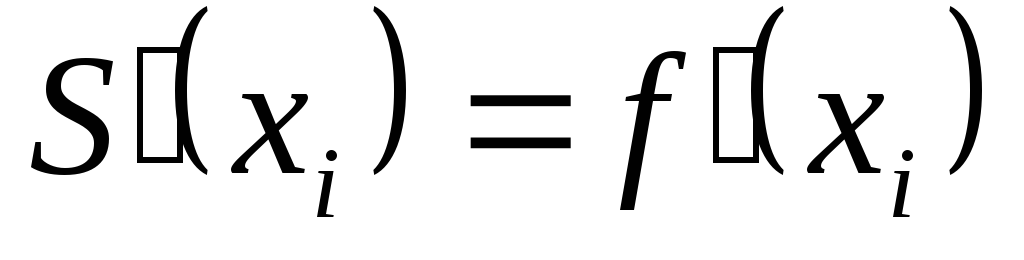 ,
,
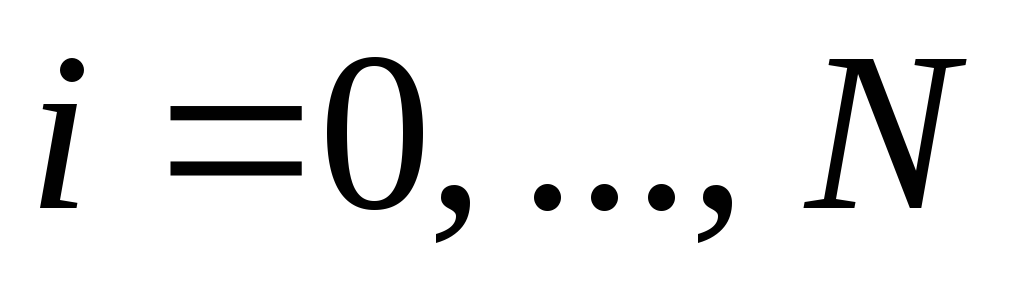 .
.
Эрмитовы сплайны являются локальными.
Для их вычисления на отрезке
![]() достаточно использовать третье условие
определения:
достаточно использовать третье условие
определения:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
тогда
,
тогда
![]() на отрезке
на отрезке
![]() можно записать:
можно записать:
![]() ,
где
,
где
![]() ,
,
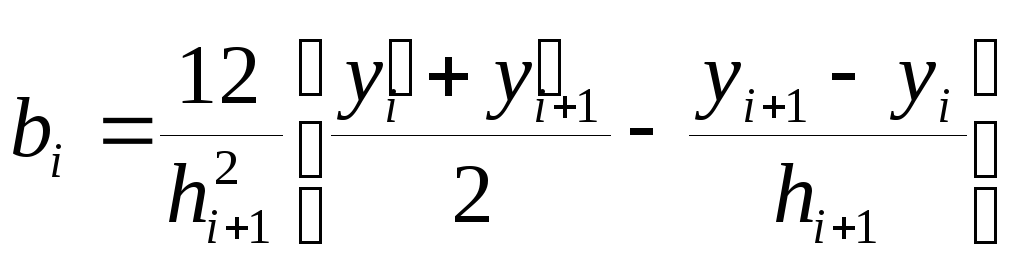 .
.
2. Кубические нелокальные сплайны
Пусть на сетке
![]() заданы
заданы
![]() ,
,
![]() .
.
Определение. Функция
![]() называется кубическим сплайном,
интерполирующим функцию
называется кубическим сплайном,
интерполирующим функцию
![]() в узлах сетки
в узлах сетки
![]() ,
если выполняются следующие условия:
,
если выполняются следующие условия:
-
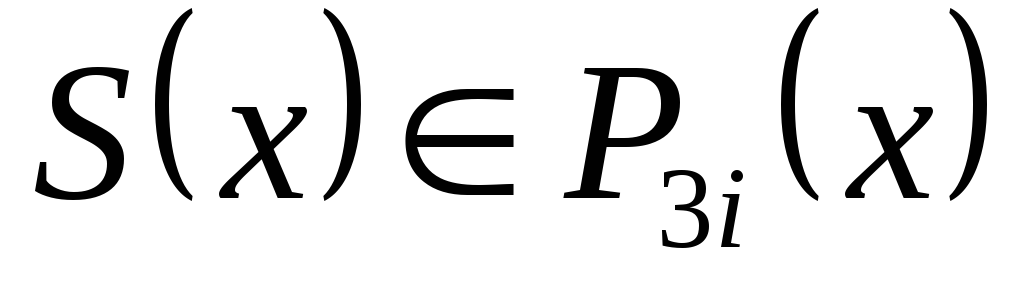 ,
для
,
для
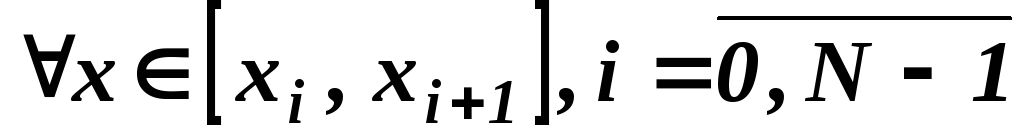 ,
, -
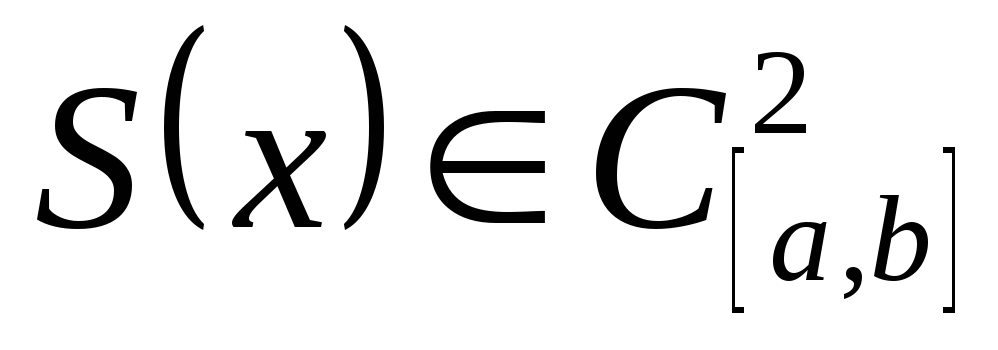 ,
(т.е. непрерывны
,
(т.е. непрерывны
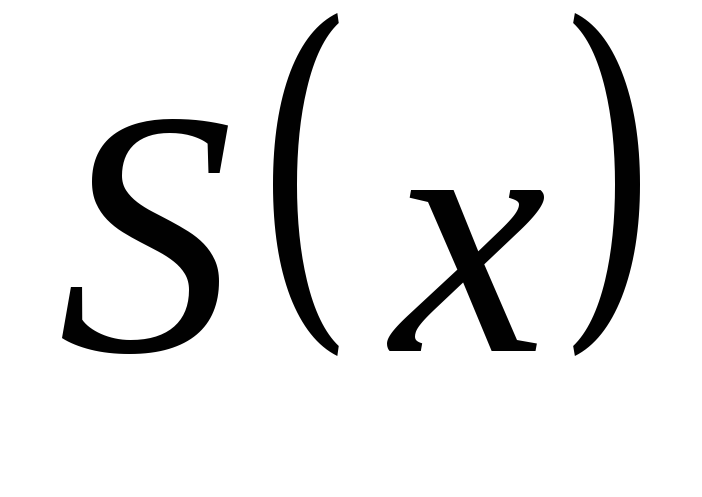 ,
,
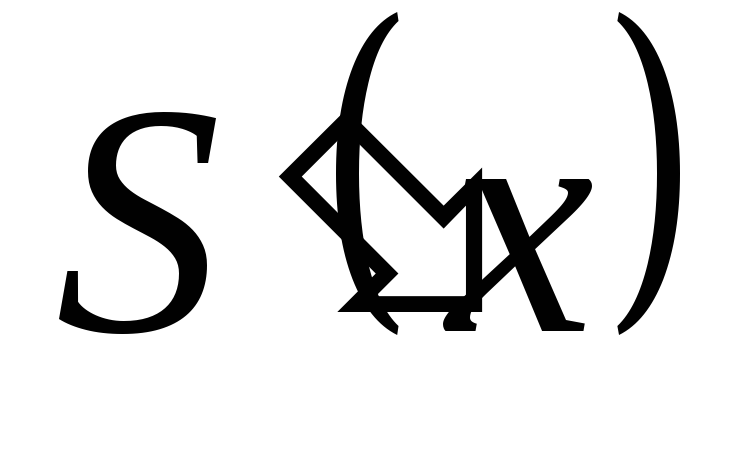 ,
,
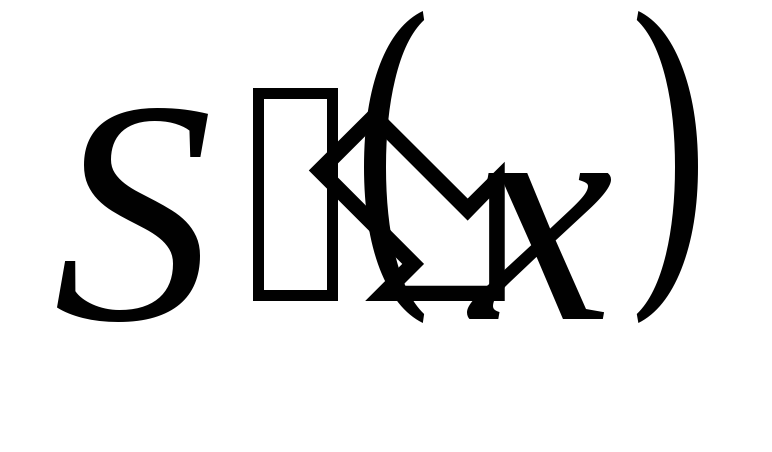 во всех внутренних узлах),
во всех внутренних узлах), -
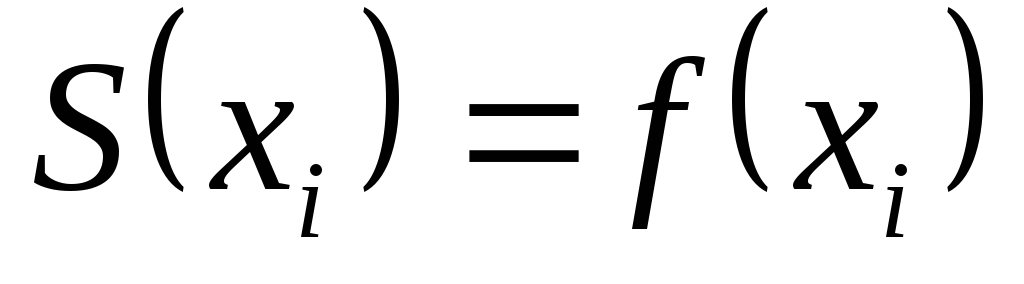 ,
,
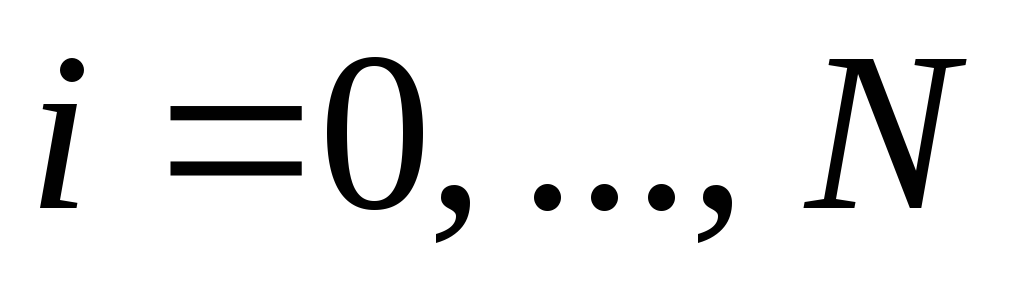 .
.
Легко показать, что этими условиями
сплайн определяется неоднозначно, а
именно, кубический сплайн, удовлетворяющий
данному определению, имеет еще 2 свободных
параметра. На каждом из N
отрезков сплайн определяется 4-мя
коэффициентами, итого, на
![]() всего
всего
![]() коэффициентов. Условие 2):
коэффициентов. Условие 2):
![]() дает
дает
![]() равенств. Условие интерполяции 1) дает
равенств. Условие интерполяции 1) дает
![]() соотношение.
соотношение.
Итого:
![]() соотношения.
соотношения.
Два недостающих дополнительных условия,
как правило, задаются в виде краевых
условий, определяющих значение сплайна
или его производных на концах отрезка
![]() :
:
-
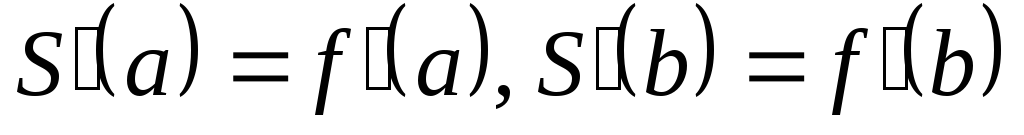 .
. -
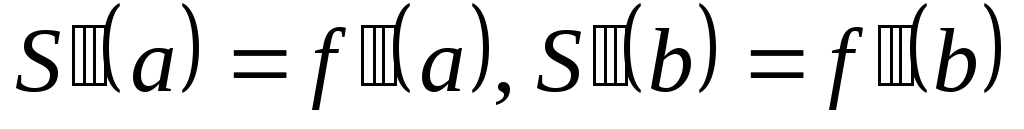 .
. -
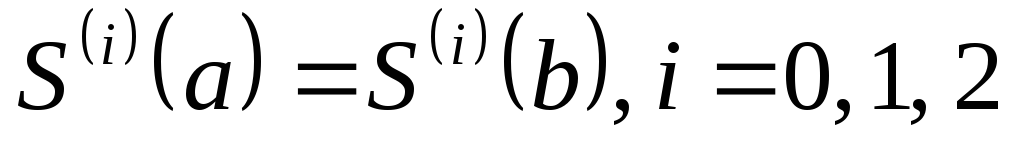 –
в этом случае говорят о периодическом
сплайне.
–
в этом случае говорят о периодическом
сплайне. -
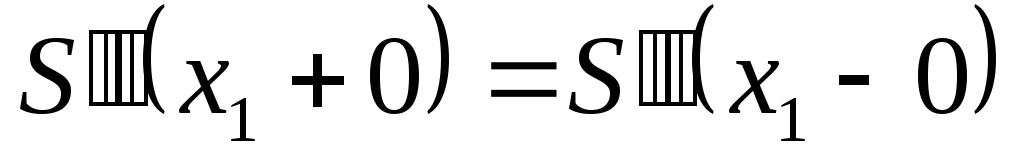 ,
,
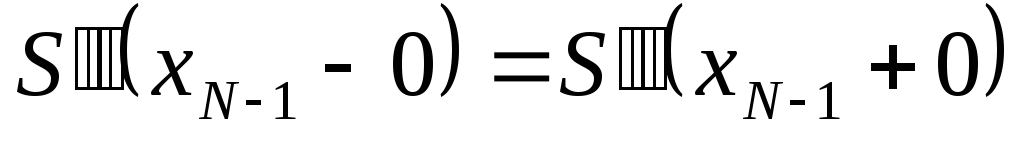 .
.
3. Построение кубического сплайна через наклоны
Кубический сплайн можно рассматривать как Эрмитов сплайн, удовлетворяющий условиям:
![]() ,
,
![]() ;
;
![]() ;
;
![]() .
.
Вводя обозначение:
![]() – наклоны,
– наклоны,
![]() ,
по построению:
,
по построению:
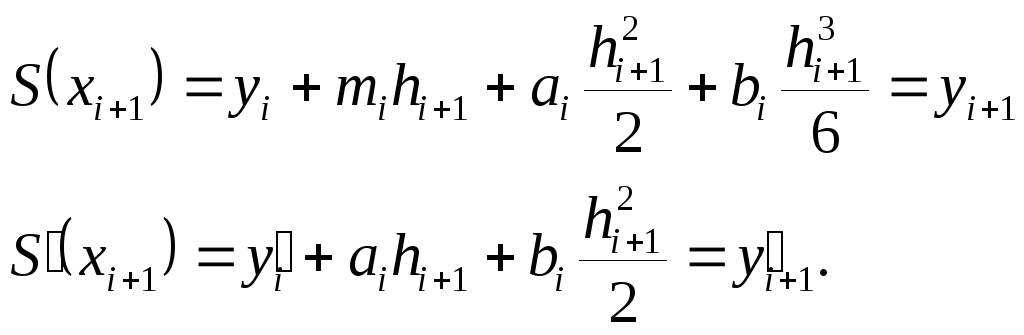
Имеем систему 2х уравнений с двумя неизвестными ai и bi, решая эту систему
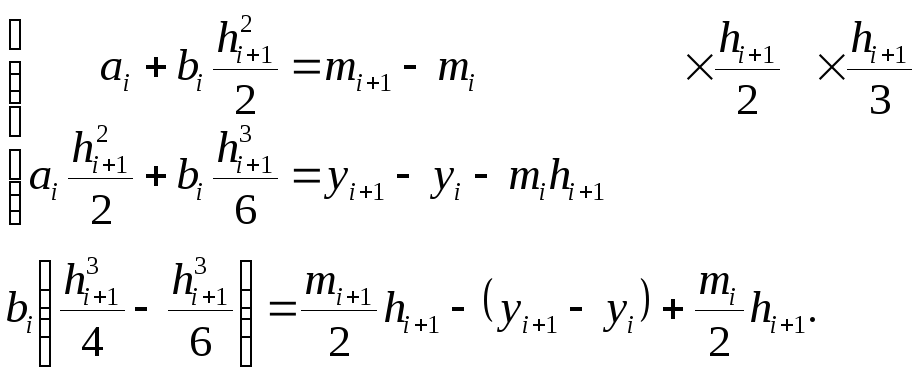
получаем выражение для bi:
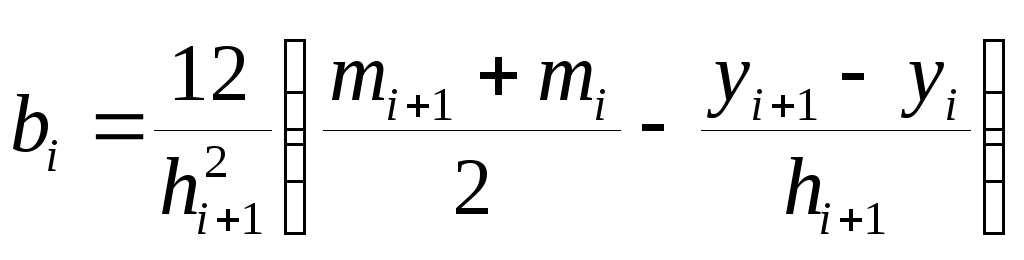
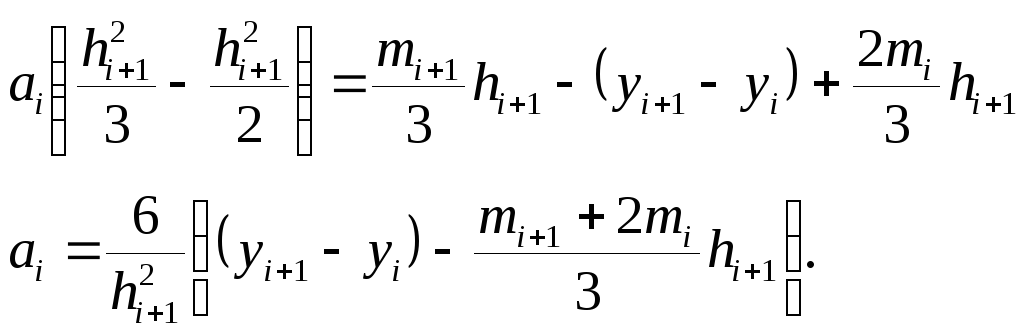
и коэффициента ai:
![]()
Из 2-ого условия определения кубического
сплайна, а именно, непрерывности 2ой
производной на
![]() ,
в том числе и в узлах сетки:
,
в том числе и в узлах сетки:
![]() на
на
![]() ;
;
![]() на
на
![]() .
.
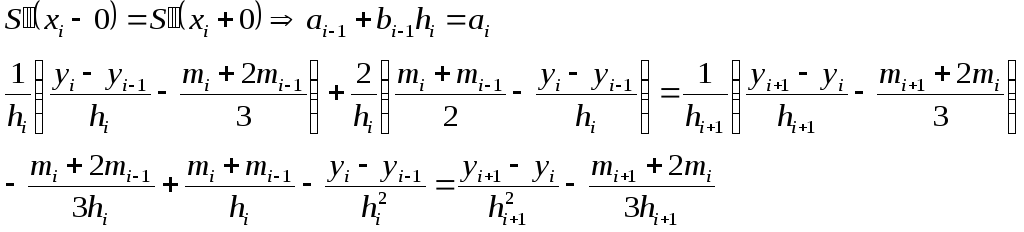
![]()
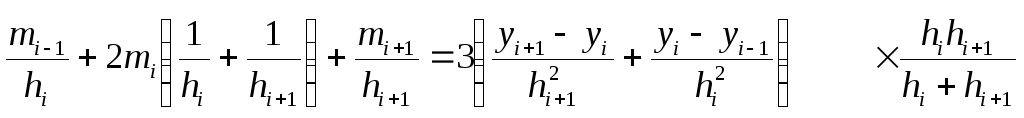
Обозначим
![]() ;
отсюда
;
отсюда
![]() .
Имеем систему N – 1
уравнения с N + 1
неизвестным
.
Имеем систему N – 1
уравнения с N + 1
неизвестным
![]() :
:
![]() .
.
Следовательно, надо добавить 2 уравнения:
1 краевое условие:
![]() ,
тогда
,
тогда
![]() .
.
2 краевое условие:
![]()
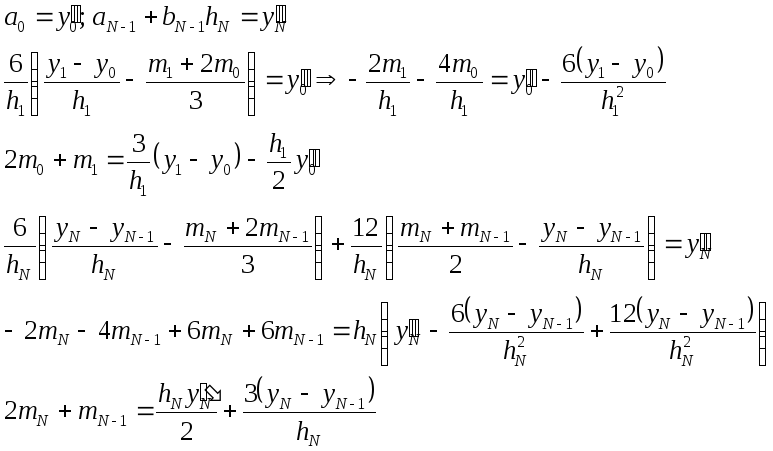
3 условие периодичности:
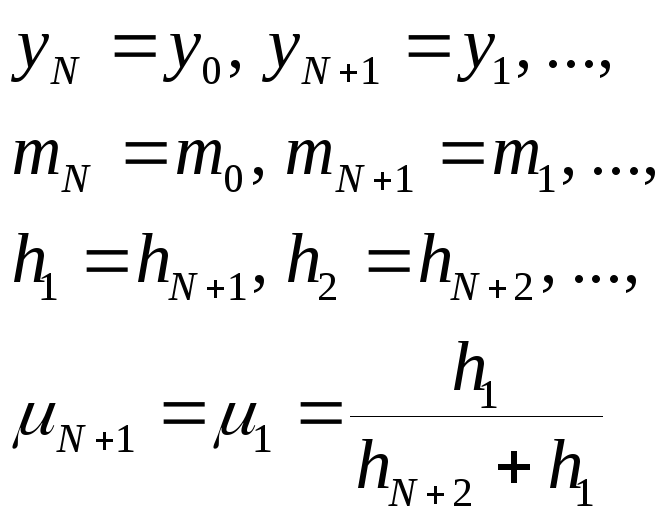
Имеем уравнение при
![]() и
и
![]() .
.
4 краевое условие:
![]()
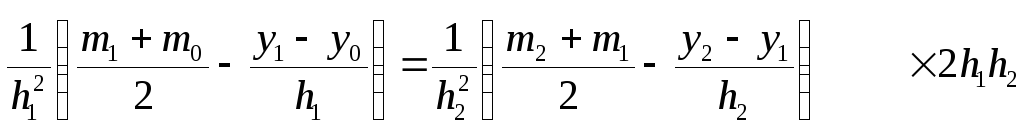
получим
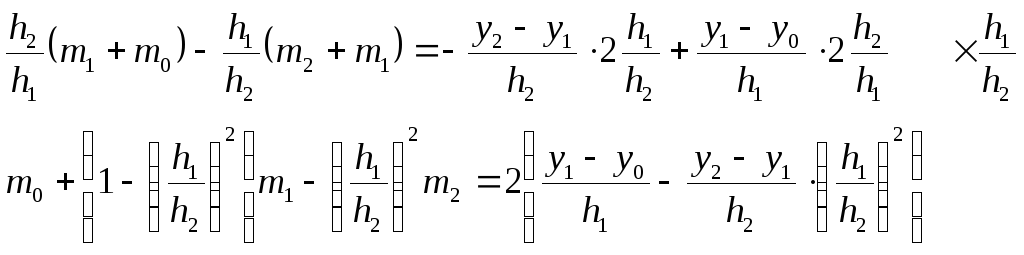
Обозначим
![]() .
.
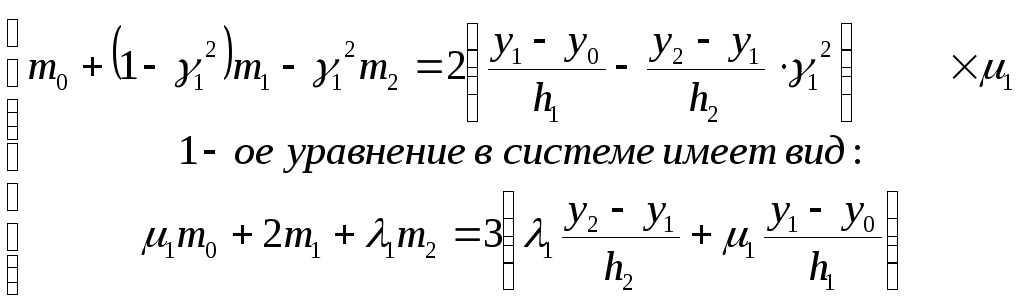
умножим 1-ое уравнение на
![]() и вычтем из второго:
и вычтем из второго:
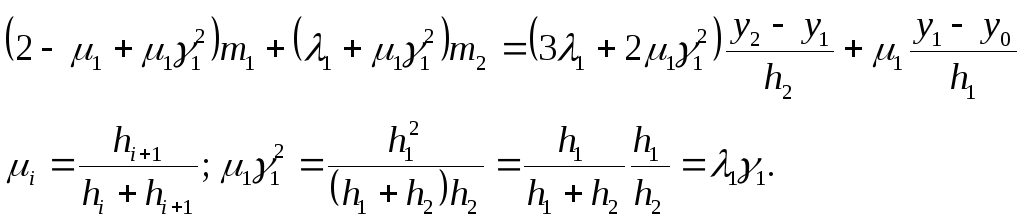
отсюда
![]()
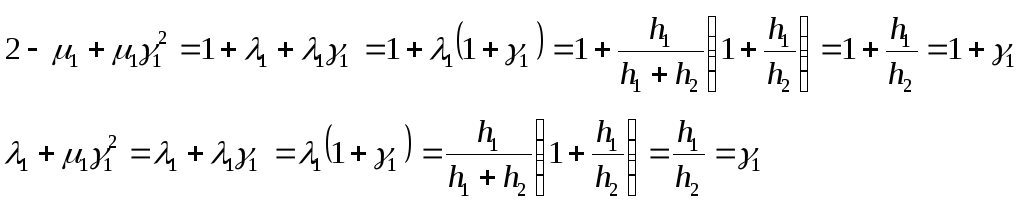
Т.о.
![]()
![]()
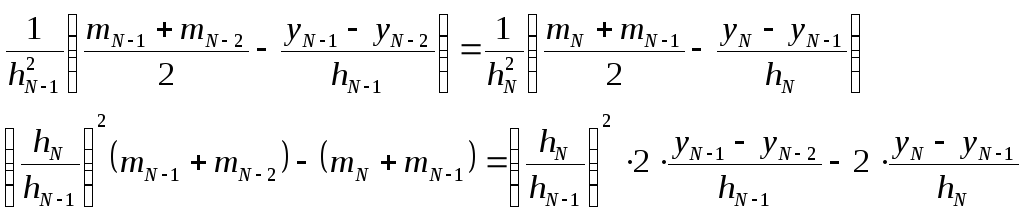
обозначим
![]()
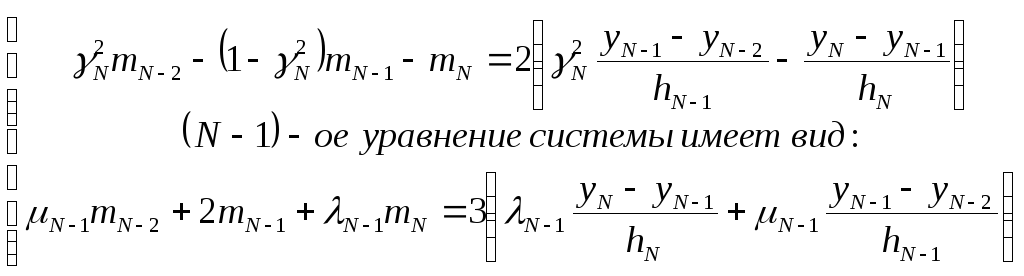
умножим 1-ое уравнение на
![]() ,
сложим 2-ое с 1-ым, получим:
,
сложим 2-ое с 1-ым, получим:
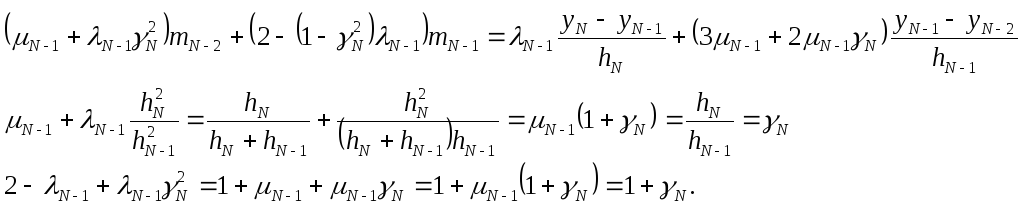
Имеем:
![]()
Итак, в случае краевых условий 4-ого типа имеем:
![]() ;
;
![]() ;
;
![]() .
.
4. Построение кубического сплайна через моменты
Моментами называются
![]()
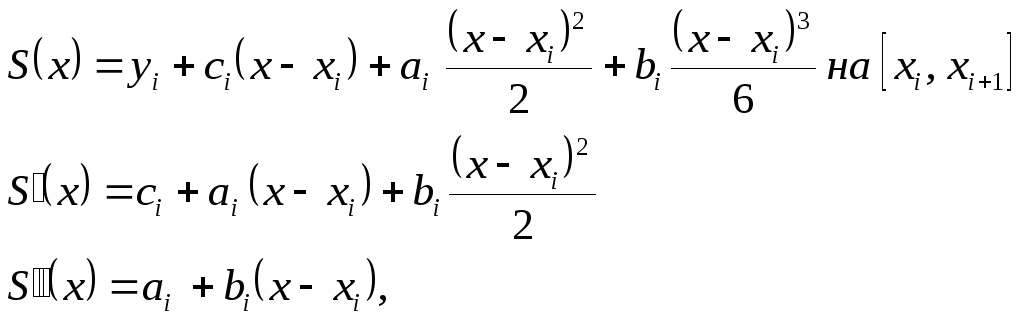
но
![]()
![]() .
.
Отсюда:
![]() ,
тогда
,
тогда
![]() .
.
Из условия непрерывности первой
производной для
![]() в узлах
в узлах
![]() ,
имеем:
,
имеем:
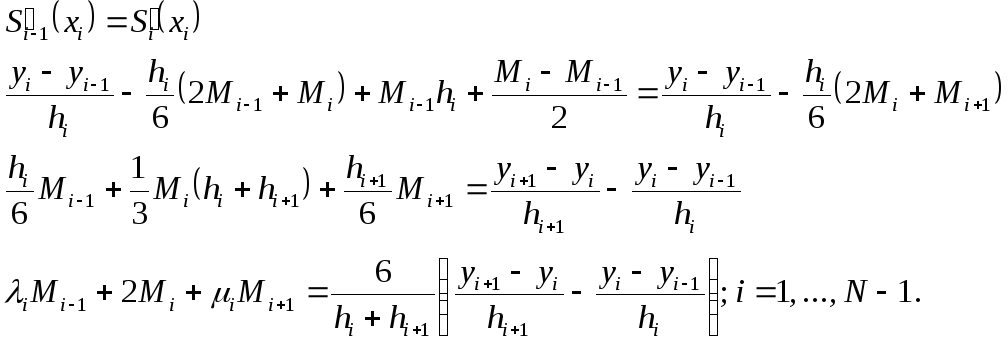
Для полученной замкнутой системы для определения моментов нужно добавить краевые условия:
-
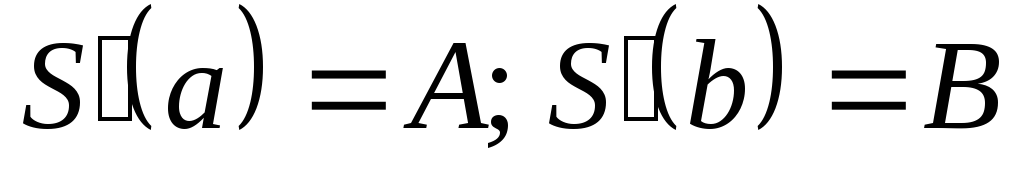 .
.
![]() ;
;
![]()
![]()
![]()
Отсюда
![]()
-
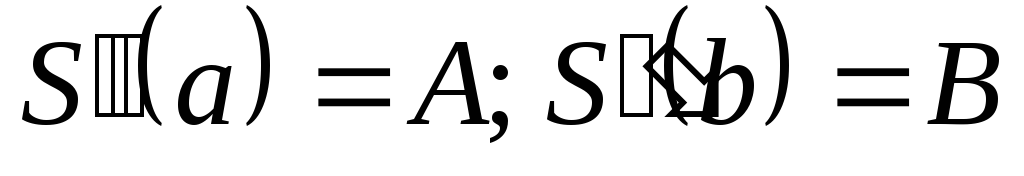 .
.
![]()
-
Периодические условия:
![]()
-
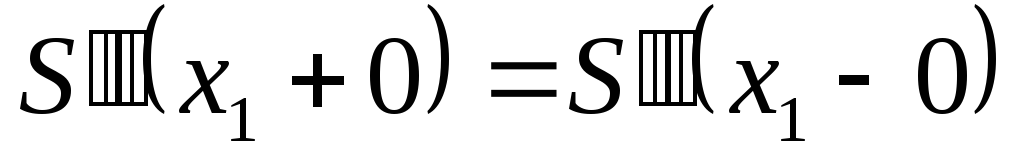 ,
,
 ;
;
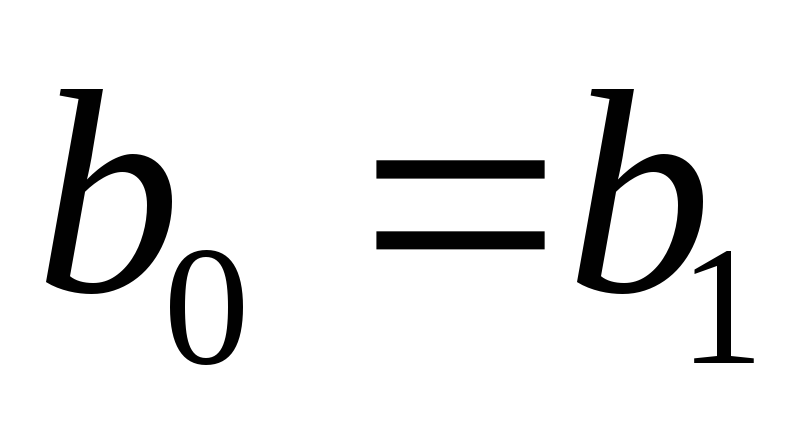 .
.
![]() .
Обозначим
.
Обозначим
![]() .
Отсюда
.
Отсюда
![]() .
.
Первое уравнение системы имеет вид:
![]() .
.
Умножим 1-ое уравнение на
![]() и
вычтем из 2-го уравнения:
и
вычтем из 2-го уравнения:
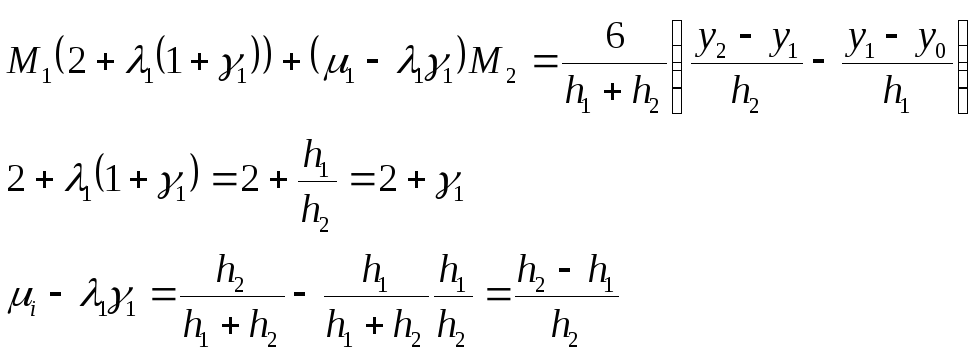
Итак,
![]()
Краевое условие:
![]()
![]() .
Обозначим
.
Обозначим
![]() .
.
![]()
![]() -ое
уравнение системы имеет вид:
-ое
уравнение системы имеет вид:
![]() .
.
Умножим 1-ое уравнение на
![]() и сложим со 2-ым:
и сложим со 2-ым:
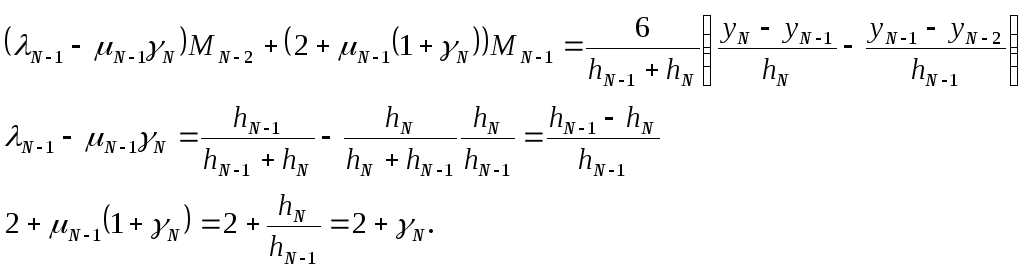
Итак,
![]()
5. Дифференцирование и интегрирование кубического сплайна
1. Если сплайн
![]() определен через наклоны
определен через наклоны
![]() ,
то вычисление
,
то вычисление
![]() не представляет труда, т. к.
не представляет труда, т. к.
![]() ;
;
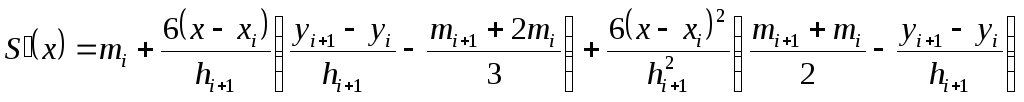 ;
;
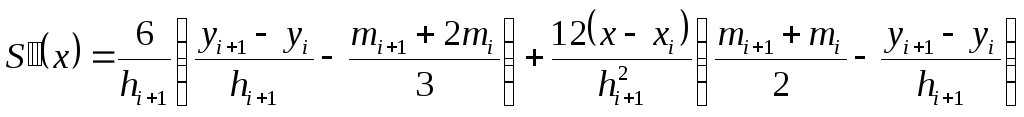 ;
;
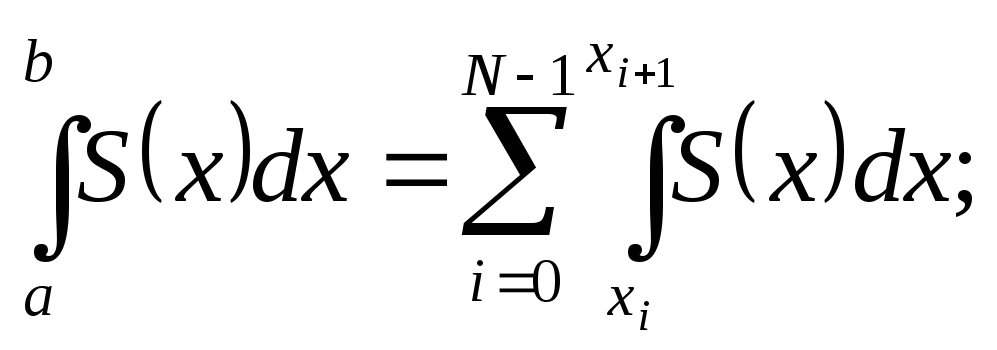
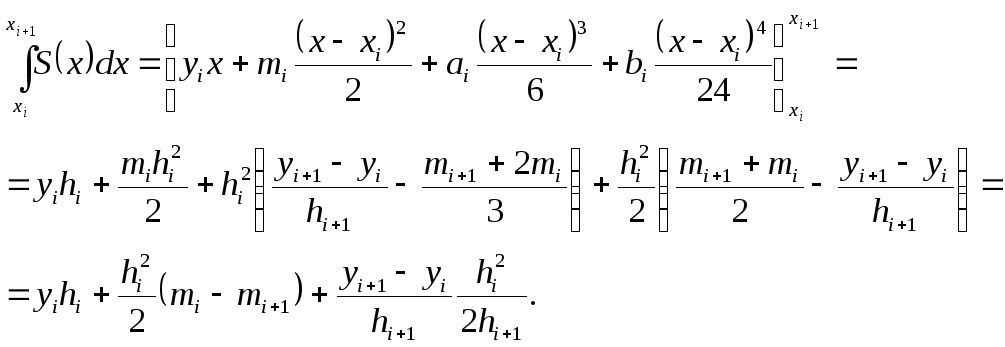
2. Если сплайн
![]() определен через наклоны
определен через наклоны
![]() ,
то
,
то
![]() ;
;
![]() ;
;
![]() ;
;
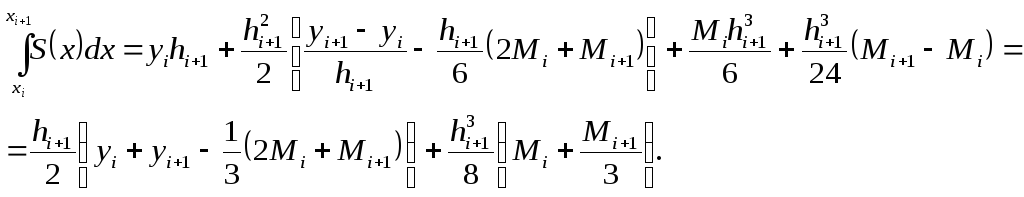
6 Варианты заданий
Построение сплайна через наклоны
|
1й тип краевых условий |
2-й тип краевых условий |
4-й тип краевых условий |
|
|
1 |
9 |
17 |
Задача интерполирования, данные из лаб. раб. 1 |
|
2 |
10 |
18 |
Задача интегрирования, данные из лаб. раб. 4 |
|
3 |
11 |
19 |
Задача дифференцирования (первая производная), данные из лаб. раб. 1 |
|
4 |
12 |
20 |
Задача дифференцирования (вторая производная), данные из лаб. раб. 1 |
Построение сплайна через моменты
|
1й тип краевых условий |
2-й тип краевых условий |
4-й тип краевых условий |
|
|
5 |
13 |
21 |
Задача интерполирования, данные из лаб. раб. 1 |
|
6 |
14 |
22 |
Задача интегрирования, данные из лаб. раб. 4 |
|
7 |
15 |
23 |
Задача дифференцирования (первая производная), данные из лаб. раб. 1 |
|
8 |
16 |
24 |
Задача дифференцирования (вторая производная), данные из лаб. раб. 1 |
в поле таблицы номер варианта.
