Решение слау размерности

1. Метод Крамера.

Рассмотрим систему из двух уравнений с двумя неизвестными:

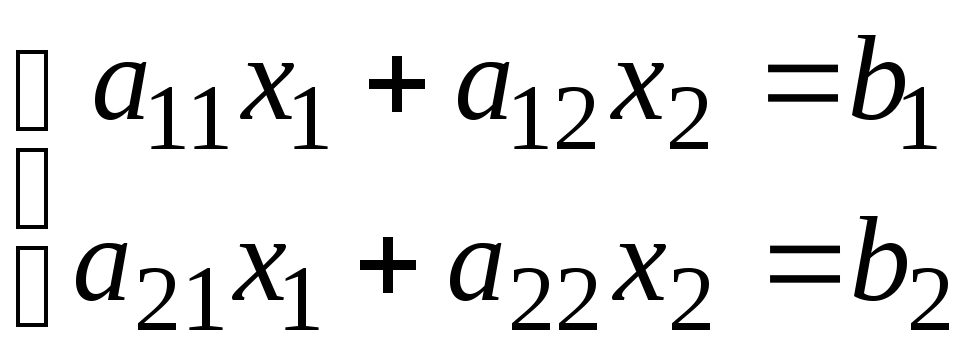
Выразим в системе переменную избавившись от переменной.

Поделим первое уравнение на элемент и умножим полученный результат на.

,

Складываем со вторым уравнением системы и выражаем переменную .

.

В полученной дроби в числителе стоит определитель , а в знаменателе основной определитель системы.

И мы получили формулу . Аналогичными вычислениями мы получим, где.

Рассмотрим правило Крамера для системы уравнений , наложив условие линейной независимости уравнений системы.

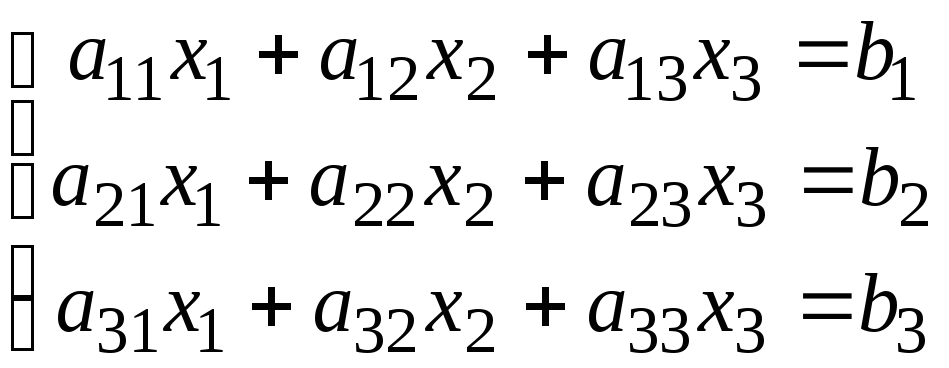
Кроме основного определителя системы введем в рассмотрение дополнительные определители, получаемые заменой коэффициентов -го столбца столбцом свободных членов.

, ,

.

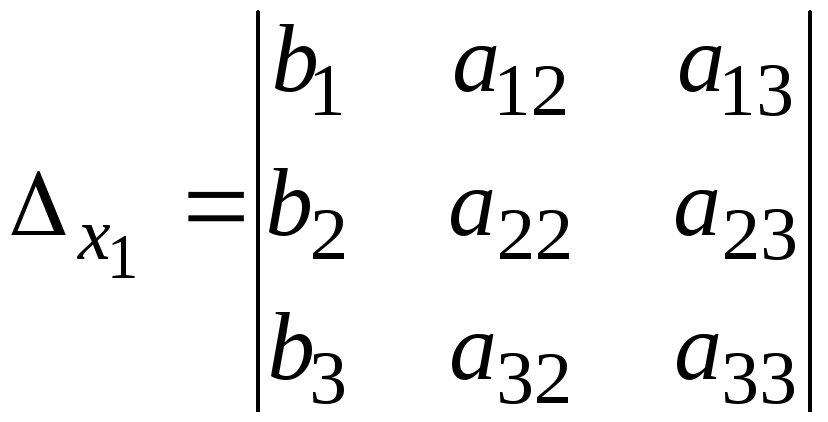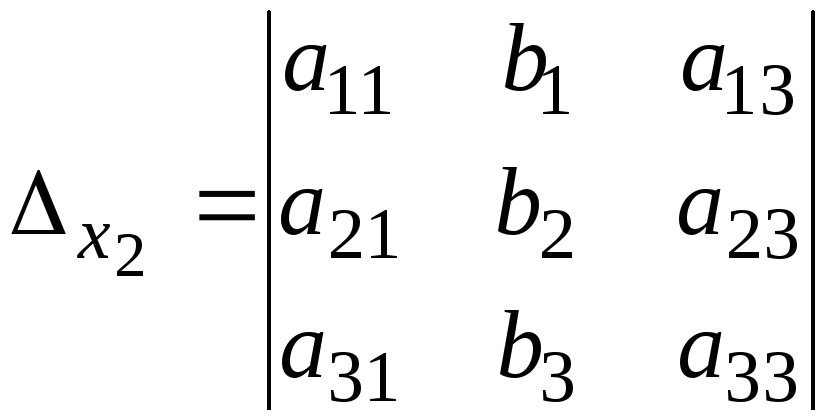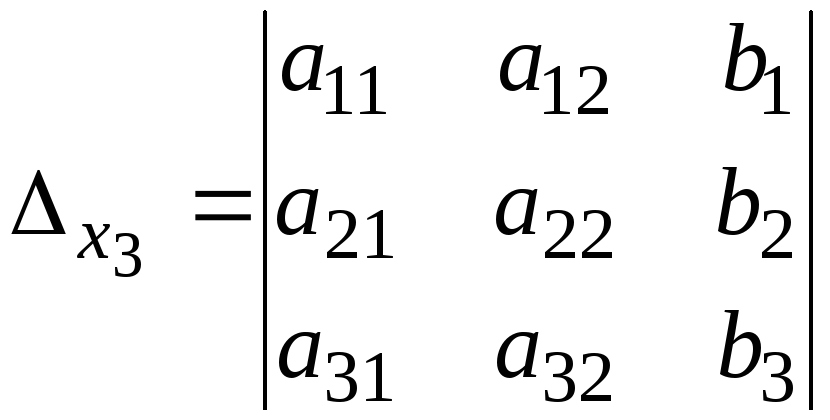Умножим каждое уравнение системы на алгебраические дополнения первого столбца и сложим левые и правые части полученных равенств:

.

Используя следствие свойстваопределителей получаем:

или .

Поступая аналогичным образом получим следующие формулы Крамера для определения неизвестных системы:

, ,.

Теорема (формулы Крамера): Система из n уравнений с n неизвестными

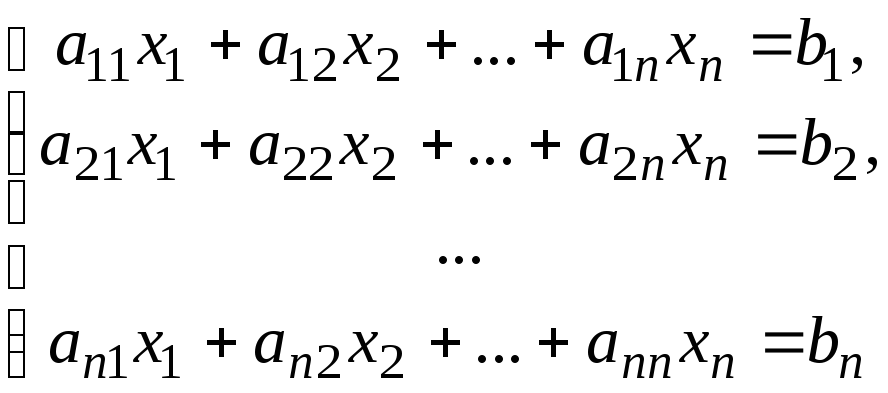
в случае, когда определитель системы отличен от нуля , имеет единственное решение определяемое формулами:

(14.6)

(для всех ), где черезобозначен определитель основной матрицы системы, а- дополнительные определители, получаемые из Δ заменой-го столбца столбцом свободных членов, т.е.

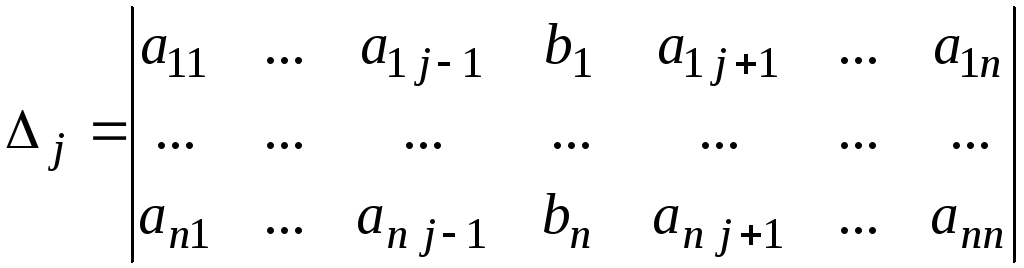(14.7)

2) Метод Гаусса.

Метод Гаусса относится к наиболее эффективным методам решения СЛАУ. Этим методом решаются как квадратные, так и прямоугольные системы линейных уравнений. В основе метода Гаусса лежат прямой и обратный ход. Прямым ходом расширенную матрицу системы элементарными преобразованиями сводят к треугольному виду. Обратным ходом находят неизвестные величины.

К элементарным преобразованиям относится:

1. Перестановка двух любых уравнений системы;

2. Умножение любого уравнения системы на произвольное, отличное от нуля, число;

3. Прибавление к произвольному уравнению системы любого другого уравнения, умноженного на произвольное число.

Методом Гаусса можно решать и прямоугольные системы.

Лекция 15

Обратная матрица, матричный метод решения системы. Общее решение системы.

Цель: изучить понятие обратной матрицы, ее свойства и метод вычисления. Изучить матричный метод решения СЛАУ.

Определение. Квадратная матрица называетсяобратной к матрице , если

(15.1)

, - единичная матрица.- является единственной для.

Определение. Матрица - называетсянеособенной (невырожденной или несингулярной) матрицей, если . В противном случае-особенная (вырожденная или сингулярная).

Теорема. Всякая неособенная матрица имеет обратную матрицу.

Доказательство. Рассмотрим матрицу ,. Введем в рассмотрение матрицу, называемуюсоюзной матрицей элементами которой служат алгебраические дополнения матрицы . Рассмотрим матрицу, вычислим произведение:

,

где .

Аналогично, .

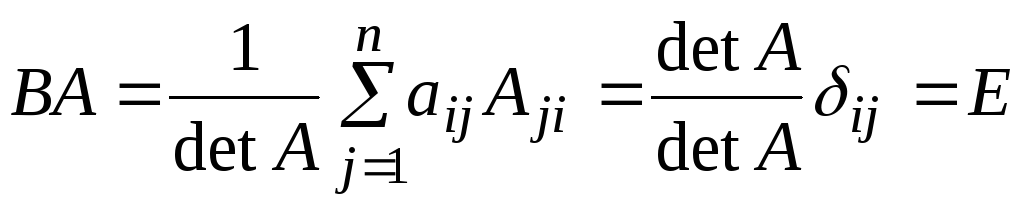Следовательно, - по определению, таким образом,

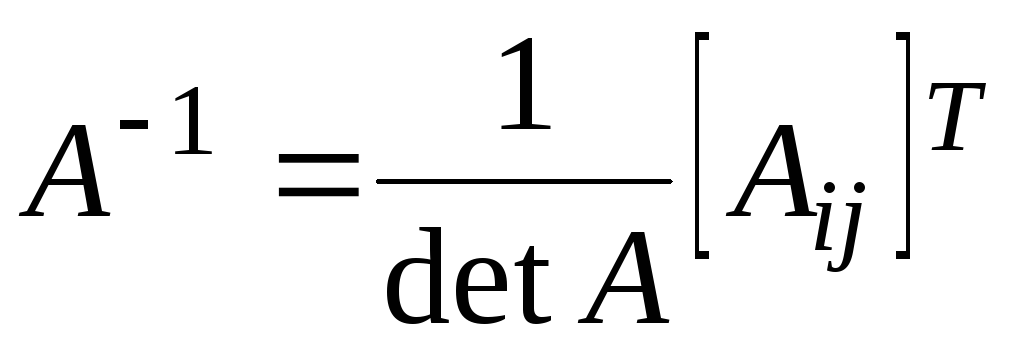(15.2)

Пример. Вычислить обратную матрицу

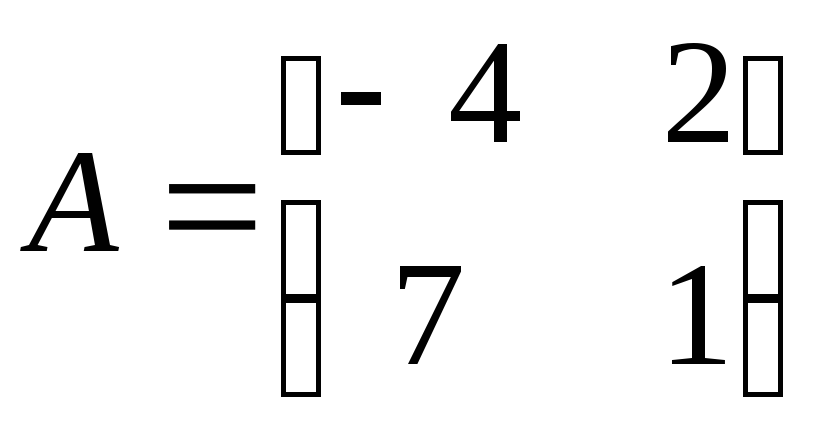
Решение.

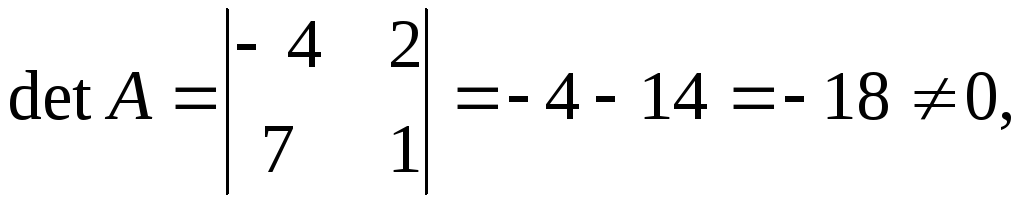
следовательно, обратная матрица существует. Вычисляем соответствующие алгебраические дополнения

, ,

Итак, .

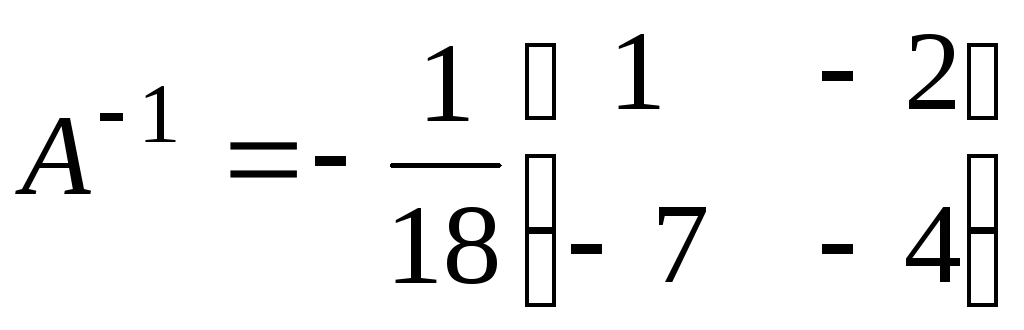Свойства обратной матрицы

1) ;

2) ;

3) если- неособенные матрицы одного порядка.

Определение. Действительная квадратная матрица , удовлетворяющая условию, называетсяортогональной матрицей, .

Определение. Следом – квадратной матрицыназывается сумма всех её диагональных элементов:.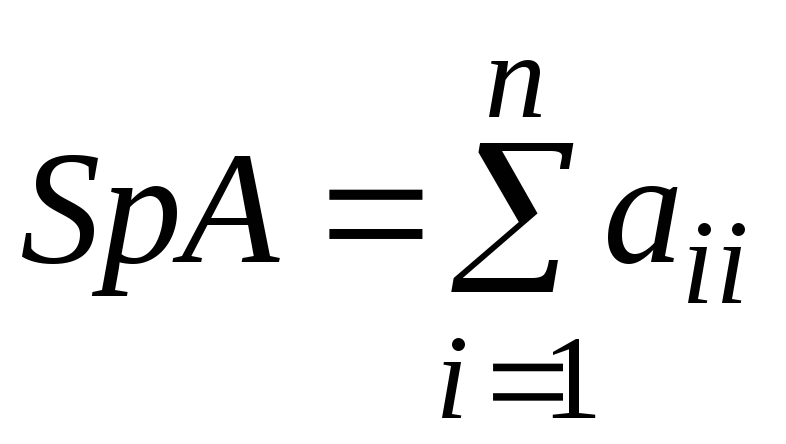

Матричный метод решения СЛАУ.

Если определитель основной матрицы системы отличен от нуля, то ее решение определяется формулой:

(15.3)

Где - обратная к основной матрице системы, вычисляемая по формуле.

Совместность однородной и неоднородной СЛАУ.

Рассмотрим однородную СЛАУ

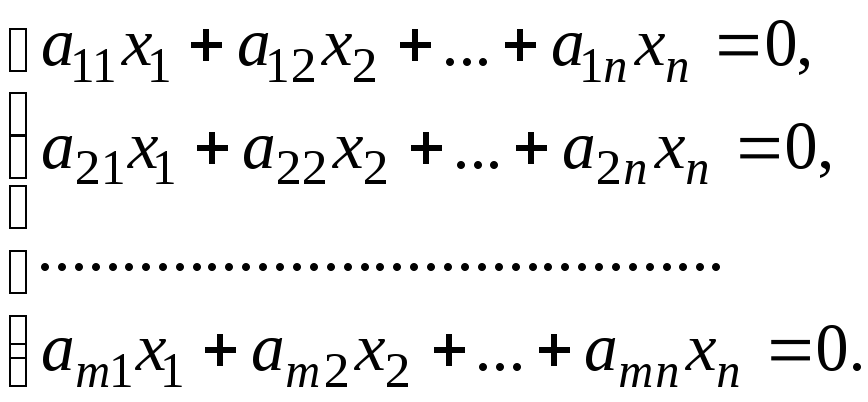
система всегда имеет хотя бы одно решение, например, тривиальное решение .

Когда однородная СЛАУ имеет решения отличные от нулевого?

Заметим, что существует нетривиальное решение ~ линейной зависимости столбцов матрицы однородной СЛАУ (по определению линейной зависимости это означает существует что является уравнениями системы), но по теореме о базисном миноре линейная зависимость имеет место тогда и только тогда когда порядокбазисного минора меньше числаеё столбцов. Отсюда теорема.

Теорема. Однородная СЛАУ имеет нетривиальное решение тогда и только тогда, когда ранг матрицы системы меньше числаеё столбцов.

Следствие. Квадратная однородная система имеет нетривиальное решение тогда и только тогда, когда определитель матрицы этой системы равен нулю.