
Геометрический смысл комплексного числа
Комплексное
число
![]() изображается в плоскости
изображается в плоскости![]() точкой
точкой![]() с координатами
с координатами![]() либо вектором, начало которого находится
в точке
либо вектором, начало которого находится
в точке![]()
![]() ,
а конец в точке
,
а конец в точке![]() (рис. 1.3).
(рис. 1.3).
Длина
![]() вектора
вектора![]() называетсямодулем
комплексного числа и обозначается
называетсямодулем
комплексного числа и обозначается
![]() (2.3)
(2.3)
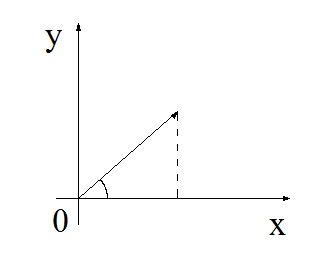
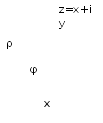
Рис. 2.1
Угол
![]() ,
образованный положительным направлением
оси ОХ и вектором
,
образованный положительным направлением
оси ОХ и вектором![]() ,
называетсяаргументом
комплексного числа и обозначается
,
называетсяаргументом
комплексного числа и обозначается
![]()
![]() ,
где
,
где
![]() –главное
значение аргумента,
–главное
значение аргумента,
![]() .
Главное значение аргумента комплексного
числа может быть найдено с помощью
формулы:
.
Главное значение аргумента комплексного
числа может быть найдено с помощью
формулы:
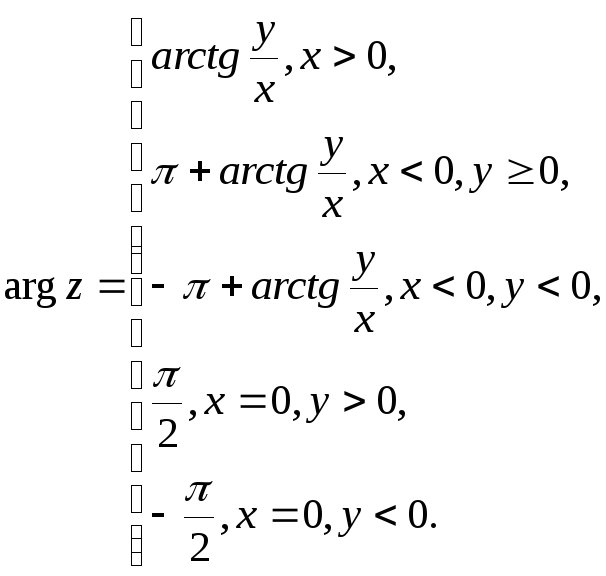 (2.5)
(2.5)
Если в алгебраической форме записи комплексного числа вместо декартовых координат точки подставить их полярное представление (1.4), то получим тригонометрическое представление комплексного числа.
Определение. Каждое комплексное число, отличное от нуля, можно записать в тригонометрической форме
![]() (2.6)
(2.6)
где
![]() .
.
С помощью формулы Эйлера:
![]() (2.7)
(2.7)
каждое комплексное число может быть записано в показательной форме
![]() . (2.8)
. (2.8)
Число
![]() называетсясопряженным
комплексному
числу
называетсясопряженным
комплексному
числу
![]() .
.
Выполняются
следующие равенства:
![]() ;
;
![]() ;
;
![]() ;
;
Аналогично
доказывается, что
![]() ;
;![]() ;
;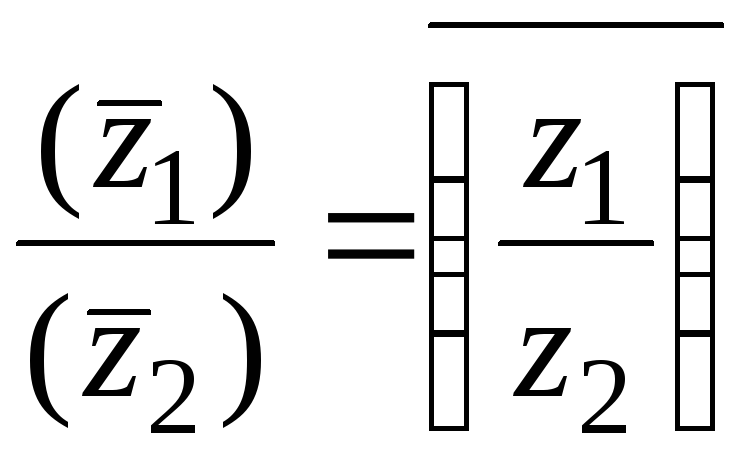 .
.
Важно
знать, что ![]() (2.9)
(2.9)
Операции над комплексными числами, заданными в алгебраической форме
Определение.
Два
комплексных числа называются равными,
если у них совпадают действительные и
мнимые части, т.е.
![]() ,
если
,
если![]() и
и![]() .
.
Сложение и вычитание
Действие
сложения и вычитания комплексных чисел
![]() и
и![]() производится по правилу сложения и
вычитания двучленов
производится по правилу сложения и
вычитания двучленов
![]() .
.
Группируя отдельно действительную и мнимую части, получим формулу:
![]() (2.10)
(2.10)
Умножение.
Действие
умножение комплексных чисел
![]() и
и![]() производится по правилу умножения
двучленов
производится по правилу умножения
двучленов
![]()
раскроем скобки
![]()
используя формулу (2.2) и группируя действительные и мнимые слагаемые, получим выражение:
![]() (2.11)
(2.11)
Деление.
Чтобы
преобразовать дробь
![]() в комплексное число, необходимо числитель
и знаменатель дроби умножить на число
сопряжённое к знаменателю, в числителе
произвести действие умножения, а для
знаменателя воспользоваться формулой
(2.9)
в комплексное число, необходимо числитель
и знаменатель дроби умножить на число
сопряжённое к знаменателю, в числителе
произвести действие умножения, а для
знаменателя воспользоваться формулой
(2.9)
![]() :
:
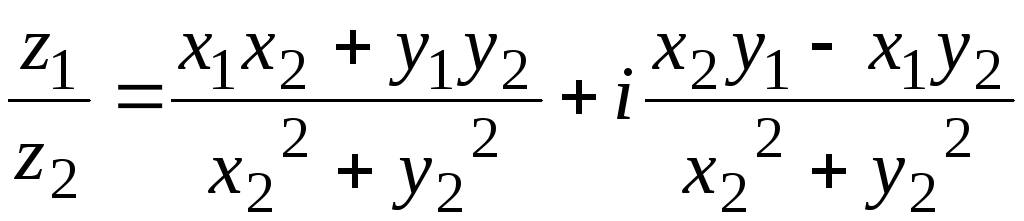 (2.12)
(2.12)
Действия над комплексными числами, заданными в тригонометрической или в показательной форме
Умножение:
При
умножении двух комплексных чисел
заданных в тригонометрической или
показательной формах их модули
перемножаются, а аргументы складываются:
![]() .
.
![]() (2.13)
(2.13)
![]() (2.14)
(2.14)
Докажем
формулу (2.14). Пусть
![]() ,
,![]() .
.
![]()
![]()
![]()
![]()
![]()
![]() ;
;
Деление:
При
делении двух комплексных чисел заданных
в тригонометрической или показательной
формах их модули делятся, а аргументы
вычитаются:
![]() ,
,![]() .
.
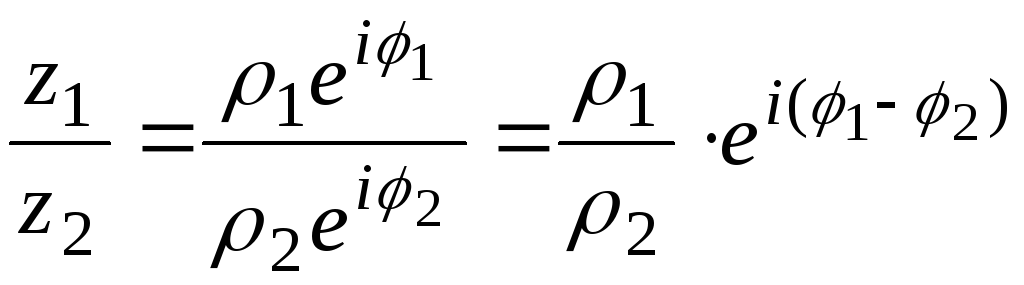 (2.15)
(2.15)
![]() (2.16)
(2.16)
Лекция 3
Понятие многочлена, корни многочленов, кратность корня, основные теоремы алгебры, следствия из теорем.
Возведение в степень.
Для
возведения комплексного числа в целую
положительную степень
![]() применяют формулу Муавра:
применяют формулу Муавра:
![]() (3.1)
(3.1)
Данная формула является следствием формулы (2.14).
Пример.
Возвести комплексное число в степень:
1)
![]() .
.
Решение.
1.
Пусть
![]() ,
тогда для комплексного числа в числителе
и знаменателе найдем модуль и аргумент
и перепишем
,
тогда для комплексного числа в числителе
и знаменателе найдем модуль и аргумент
и перепишем![]() в показательной форме, имеем
в показательной форме, имеем![]() ,
значит
,
значит![]() ,а
,а![]() ,
,![]() ,
,![]() ,
,![]() ,
тогда получим
,
тогда получим
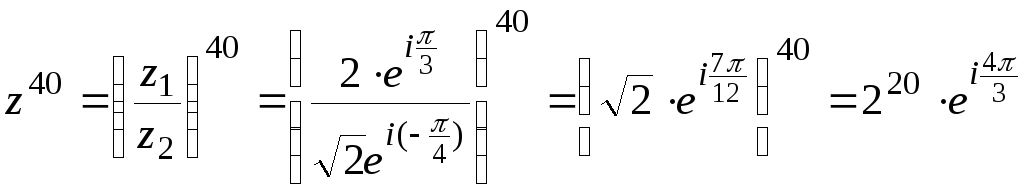
Извлечение корня порядка
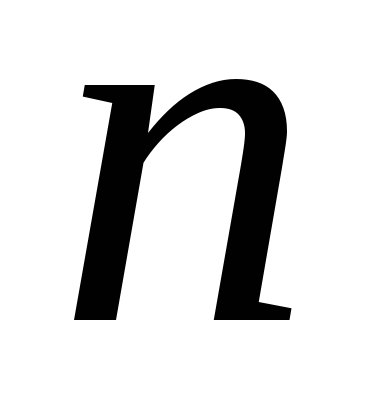 .
.
Определение.
Корнем
![]() -й
степени
из комплексного числа
-й
степени
из комплексного числа
![]() называется комплексное число
называется комплексное число![]() ,
такое что
,
такое что![]() ,
где
,
где![]() -
натуральное число. Обычно используется
обозначение
-
натуральное число. Обычно используется
обозначение![]() .
.
Корень
![]() -й
степени из комплексного числа имеет
-й
степени из комплексного числа имеет![]() различных значений, которые находятся
по формуле Муавра-Лапласа:
различных значений, которые находятся
по формуле Муавра-Лапласа:
![]() (3.2)
(3.2)
Или через показательную форму
![]() (3.3)
(3.3)
Где
![]() .
.
Точки,
соответствующие
![]() являются вершинами правильного
являются вершинами правильного![]() –
угольника, вписанного в окружность с
центром в начале координат и радиусом
–
угольника, вписанного в окружность с
центром в начале координат и радиусом![]()
![]() .
.
Способ
построения для
![]() (рис.3.1):
(рис.3.1):
Из начала координат описываем окружность радиуса
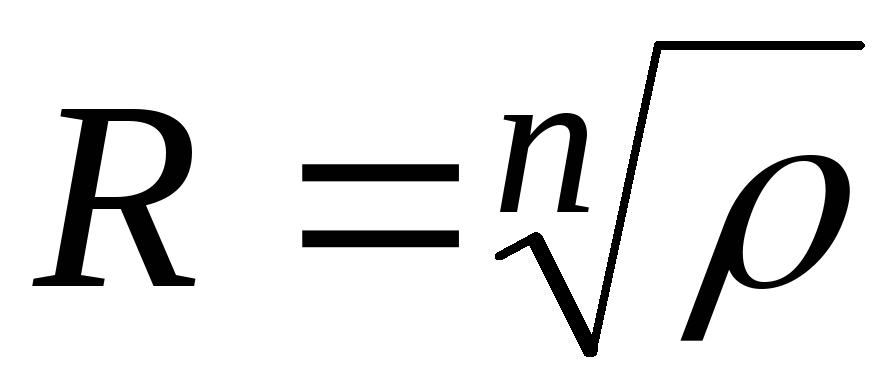 .
.Если
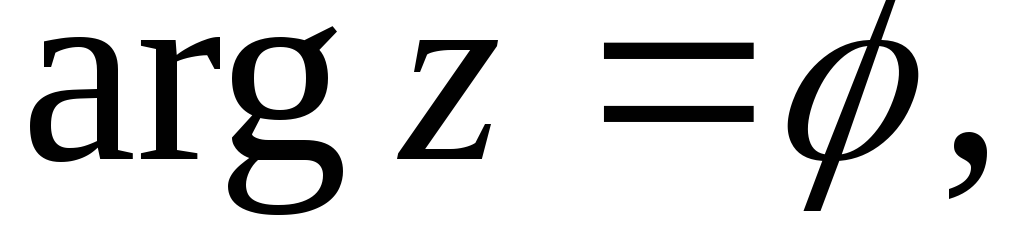 то из начала координат проводим луч
под углом
то из начала координат проводим луч
под углом к положительному направлению
к положительному направлению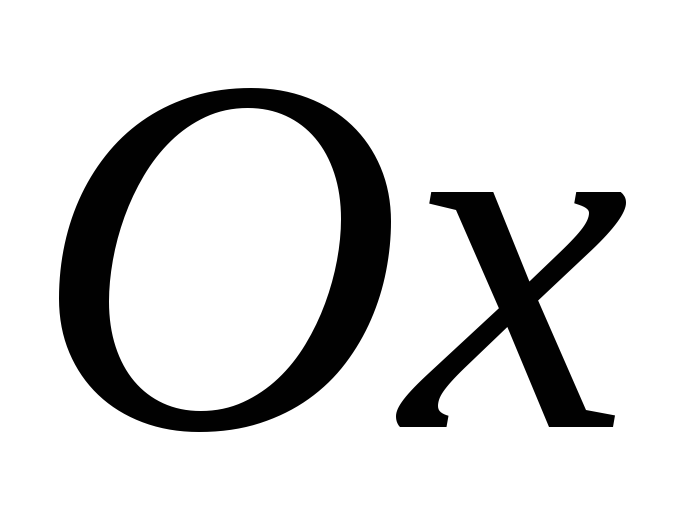 .
Пересечение луча с окружностью дает
точку
.
Пересечение луча с окружностью дает
точку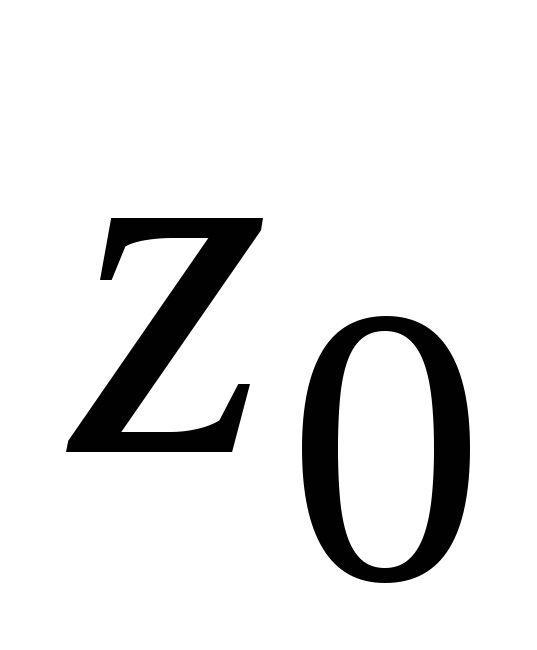 .
.Вписываем в окружность правильный
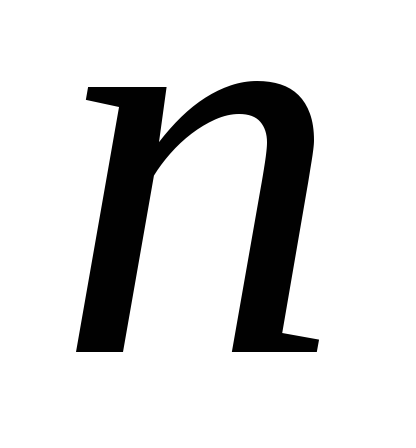 –
угольник, одна из вершин которого
найденная точка
–
угольник, одна из вершин которого
найденная точка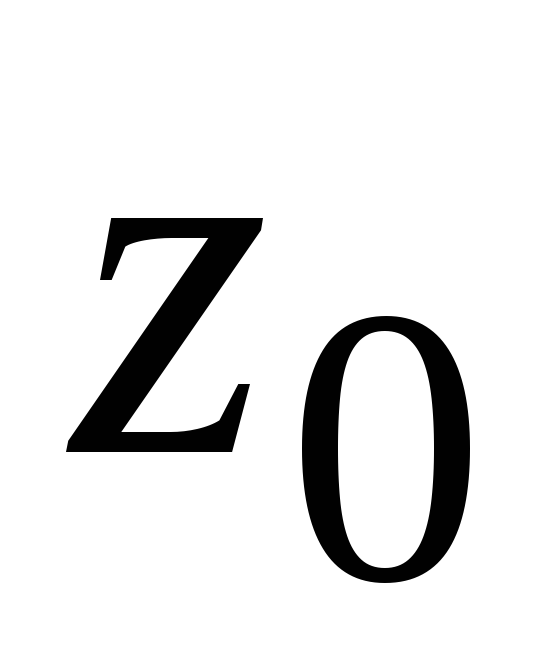 .
Точки пересечения
.
Точки пересечения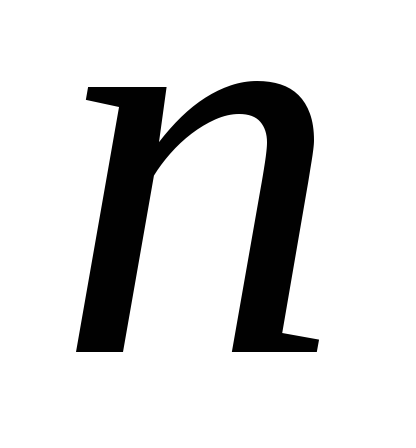 –
угольника и окружности есть решения
–
угольника и окружности есть решения .
.
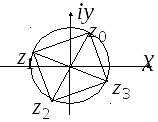
Рис. 2.2
Пример.
Найдем
все значения
![]() .
.
Решение.
Тригонометрической формой числа 1
является:
![]() .
.
Значениями
![]() являются числа:
являются числа:![]() ,
различными будут лишь корни при следующих
значениях
,
различными будут лишь корни при следующих
значениях
![]() ,
,
![]() ;
;![]() ;
;![]() .
.
Полученные
значения являются вершинами правильного
треугольника вписанного в окружность
радиуса
![]() .
.
Пример.
Корни
![]() -ой
степени из единицы
-ой
степени из единицы![]() есть вершины правильногоn-угольника,
вписанного в единичный круг.
есть вершины правильногоn-угольника,
вписанного в единичный круг.
Определение.
Многочленом
одной переменной
называется функция
![]() ,
где
,
где![]() - действительные или комплексныекоэффициенты,
а
- действительные или комплексныекоэффициенты,
а
![]() - целое неотрицательное число. Если
- целое неотрицательное число. Если![]() ,
,![]() называютстепенью
многочлена и обозначают
называютстепенью
многочлена и обозначают
![]() ,
а
,
а![]() -старшим
коэффициентом. Многочлен
-старшим
коэффициентом. Многочлен
![]() называетсянулевым,
если все его коэффициенты равны нулю.
Коэффициент
называетсянулевым,
если все его коэффициенты равны нулю.
Коэффициент
![]() при
при![]() в нулевой степени называютпостоянным
или свободным
членом.
в нулевой степени называютпостоянным
или свободным
членом.
Многочлены
степени
![]() называются соответственнолинейными,
квадратичными
(или квадратными),
кубичными
и т.д. В дальнейшем рассматриваются
только действительные коэффициенты
называются соответственнолинейными,
квадратичными
(или квадратными),
кубичными
и т.д. В дальнейшем рассматриваются
только действительные коэффициенты
![]() .
.
Определение.
Корнем
многочлена
![]() называется такое
называется такое![]()
![]() ,
при котором
,
при котором
![]() .
.
Основная теорема алгебры. Всякий многочлен положительной степени имеет, по крайней мере, один корень действительный или комплексный.
Деление многочленов. Из курса элементарной алгебры известен метод деления уголком для целых чисел, аналогичный алгоритм имеет место и для многочленов.
Пусть
даны два многочлена:
![]() и
и![]() ,
где
,
где![]() и, тогда многочлену
и, тогда многочлену![]() сопоставляется одна и только одна пара
многочленов
сопоставляется одна и только одна пара
многочленов![]() ,
для которых
,
для которых![]() ,
,![]() ,
,![]() называютчастным
деления, а
называютчастным
деления, а
![]() -остатком.
-остатком.
Если
![]() ,
тогда говорят, что
,
тогда говорят, что![]() делится
на
делится
на
![]() .
.
Если
многочлены имеют действительные
коэффициенты, то
![]() и
и![]() также имеют действительные коэффициенты.
также имеют действительные коэффициенты.
Пример.
Проверить, делится ли многочлен
![]() на
на![]() .
.
Решение. Разделим многочлены столбиком, т.е.
_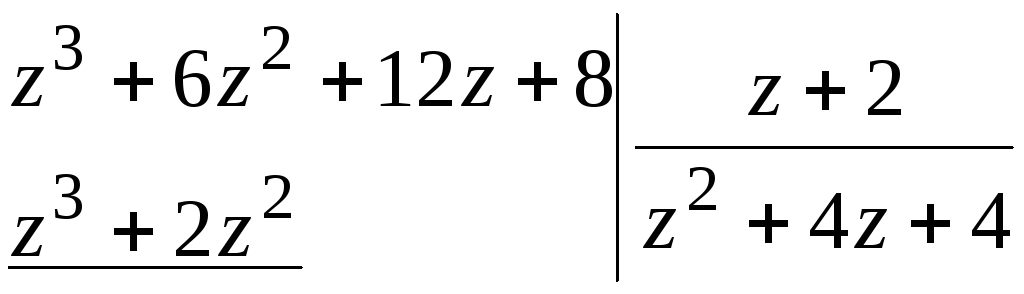
_![]()
_![]()
![]() :
:
Итак,
многочлен
![]() делится на
делится на![]() и может быть представлен в виде
и может быть представлен в виде![]() .
.
Теорема
Безу.
Число
![]() является корнем многочлена
является корнем многочлена![]() тогда и только тогда, когда
тогда и только тогда, когда![]() делится на линейный многочлен (
делится на линейный многочлен (![]() ).
).
Доказательство.
В результате деления
![]() на (
на (![]() )
имеем
)
имеем![]() .
Степень
.
Степень![]() ,
значит
,
значит
![]() тогда
подставим
тогда
подставим
![]() в
в![]() ,
получим
,
получим![]() ,
следовательно
,
следовательно![]() и
и![]() .
.
Теорема.
При делении
![]() на
на![]() ,
остаток
,
остаток![]() ,
т.е.
,
т.е.![]() .
.
Пример.
Проверить, делится ли многочлен
![]() на
на![]() .
.
Решение. Разделим многочлены столбиком, т.е.
_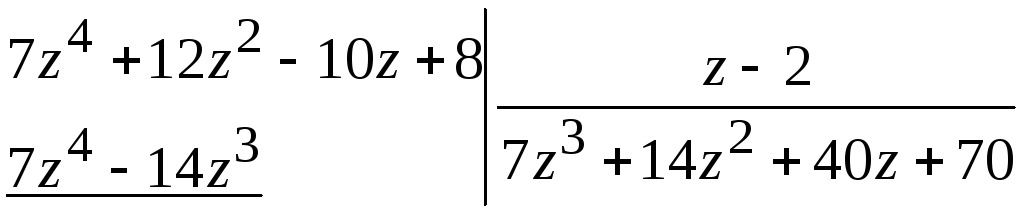
_![]()
_![]()
_![]()
![]() ;
;
степень остатка меньше степени делителя, останавливаем деление.
Итак,
многочлен
![]() не делится на
не делится на![]() и может быть представлен в виде
и может быть представлен в виде![]() .
.
Проверить,
правильно ли выполнено деление можно,
используя предыдущую теорему, согласно
которой
![]() ,
действительно,
,
действительно,![]() ,
значит деление выполнено правильно.
,
значит деление выполнено правильно.
Определение.
Число
![]() называется
называется![]() –кратным
корнем многочлена
–кратным
корнем многочлена
![]() ,
если
,
если![]() делится на
делится на![]() ,
но не делится на
,
но не делится на![]() .
Корень кратности
.
Корень кратности![]() называютпростым
корнем.
называютпростым
корнем.
Теорема.
Если
![]() - корни многочлена
- корни многочлена![]() степени
степени![]() – кратности
– кратности![]() соответственно и
соответственно и![]() ,
тогда
,
тогда![]() ,
где
,
где![]() – многочлен степени (
– многочлен степени (![]() такой, что
такой, что![]() .
.
Доказательство данной теоремы следует из теоремы Безу.
Правило определения кратности корня
Пусть
![]() –
корень кратности
–
корень кратности![]() многочлена
многочлена![]() степени
степени![]() ,
тогда
,
тогда
![]()
![]() ,
где
,
где
![]() и
и![]()
![]() ,
где
,
где
![]() ,
продолжая вычислять производные на
,
продолжая вычислять производные на![]() –
ом шаге получим,
–
ом шаге получим,
![]() ,
т.к.
,
т.к.
![]() ,
следовательно,
,
следовательно,
![]() ,тогда
можно предложить следующее правило для
вычисления кратности корня многочлена.
,тогда
можно предложить следующее правило для
вычисления кратности корня многочлена.
Для
того чтобы определить кратность корня
![]() многочлена
многочлена![]() ,
вычисляем значения производных
,
вычисляем значения производных![]() в точке
в точке![]() и как только
и как только![]() ,
тогда
,
тогда![]() - кратность корня.
- кратность корня.
Лекция 4
Векторная алгебра. Понятие вектора, координаты, модуль вектора. Линейные операции над векторами. Базис
Цель: Изучить понятие вектора, равенства векторов, как определяются координаты вектора его модуль, линейные операции над векторами и их свойства, понятие базиса.
Определение.
Направленный отрезок (упорядочивающий
пару точек) будем называть вектором
и
обозначать
![]() ,
,![]() ,
где точку
,
где точку![]() называютначалом
вектора, а
называютначалом
вектора, а
![]() –
егоконцом
(рис.4.1).
–
егоконцом
(рис.4.1).
Необходимо знать, что в печатных изданиях часто векторные величины и векторы обозначают жирным шрифтом, без стрелки
В
В
![]()
А
Рис. 4.1
Расстояние
между началом и концом вектора называется
его длиной,
модулем
или абсолютной величиной вектора и
обозначают
![]() ,
,![]() .
.
Векторы
называются коллинеарными,
если существует прямая, которой эти
векторы параллельны, пишут
![]() .
Коллинеарные векторы могут быть
сонаправленными (направлены в одну
сторону), и противоположно направленными.
Обозначается соответственно
.
Коллинеарные векторы могут быть
сонаправленными (направлены в одну
сторону), и противоположно направленными.
Обозначается соответственно![]() ,
,![]() .
.
Векторы называются компланарными, если существует плоскость, которой они параллельны.
Нулевой вектор считается коллинеарным любому вектору т.к. не имеет направления.
Свойство.
Если
вектор
![]() коллинеарен ненулевому вектору
коллинеарен ненулевому вектору![]() ,
то существует действительное число
,
то существует действительное число![]() такое, что
такое, что![]() .
.
Определение.
Два вектора
![]() считаютсяравными,
если выполнено три условия: 1) их модули
равны, 2) они параллельны, 3) направлены
в одну сторону.
считаютсяравными,
если выполнено три условия: 1) их модули
равны, 2) они параллельны, 3) направлены
в одну сторону.
О равенстве векторов стоит поговорить отдельно, т.к. оно существенно отличается от равенства чисел. Два равных числа могут рассматриваться как одно и тоже. С векторами все иначе.
Из курса физики известно, что сила может быть изображена вектором. Но, силы изображаемые равными направленными отрезками производят, вообще говоря различные действия. Так сила действующая на упругое тело изображается направленным отрезком, который не может быть никуда перенесен из данной точки. Т.е. он характеризуется направлением и точкой приложения и называется приложенным вектором.
Сила действуещая на абсолютно твердое тело, изображается скользящим вектором, который может быть перенесен не в любую точку пространства, а лишь вдоль прямой на которой он лежит.
Все остальные равные вектора (множество направленных отрезков, равных данному) называются свободными векторами, с которыми мы и будем работать.
Линейные операции над векторами
Определение.
Суммой
![]() называется вектор
называется вектор![]() ,
который может быть найден по следующим
правилам (рис.4.2).
,
который может быть найден по следующим
правилам (рис.4.2).
Свойства сложения векторов:
1)
![]() ,
(коммутативность);
,
(коммутативность);
2)
![]() ,
(ассоциативность);
,
(ассоциативность);
3)
прибавление нулевого вектора к любому
другому не меняет последнего
![]() ;
;
4)
вектор, противоположный
вектору
![]() ,
обозначается
,
обозначается![]() .
Их сумма дает нулевой вектор
.
Их сумма дает нулевой вектор![]() .
.
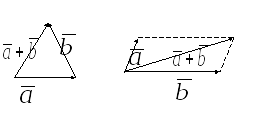
Правило треугольника Правило параллелограмма
Рис. 4.2
Определение.
Разность
![]() есть сумма
есть сумма![]() (рис.4.3).
(рис.4.3).

Рис.4.3
Определение.
Произведением вектора
![]() на вещественное число
на вещественное число![]() называется любой вектор
называется любой вектор![]() ,
удовлетворяющий следующим условиям:
,
удовлетворяющий следующим условиям:
а)
вектор
![]() коллинеарен вектору
коллинеарен вектору![]() ;
;
б)
![]() ;
;
в)
векторы
![]() и
и![]() направлены одинаково если
направлены одинаково если![]() и противоположно направлены если
и противоположно направлены если![]()
Свойства умножения вектора на число
1.
Для любых действительных чисел
![]() и любого вектора
и любого вектора![]() верно равенство
верно равенство![]() .(ассоциативность)
.(ассоциативность)
2. Умножение векторов на число дистрибутивно относительно сложения чисел
![]() (дистрибутивность).
(дистрибутивность).
3.
Умножение векторов на число дистрибутивно
относительно сложения векторов
![]()
4.
![]() .
.
Применяя линейные операции над векторами мы можем составлять суммы векторов умноженных на некоторые вещественные числа.
Определение.
Выражение вида
![]() ,
где
,
где![]() –
произвольные постоянные, называетсялинейной
комбинацией
векторов
–
произвольные постоянные, называетсялинейной
комбинацией
векторов
![]() .
.
С помощью введенных выше линейных операций мы можем преобразовать выражения, составленные из линейных комбинаций: раскрывать скобки, приводить подобные члены, переносить некоторые слагаемые в другую часть равенства с противоположным знаком.
Свойства линейной комбинации
1.
Если
![]() –
параллельны, то каждая их линейная
комбинация параллельна им.
–
параллельны, то каждая их линейная
комбинация параллельна им.
2.
Если
![]() – компланарны, то каждая их линейная
комбинация компланарна с ними.
– компланарны, то каждая их линейная
комбинация компланарна с ними.
Определение.
Пусть дана линейная комбинация
![]() ,
если
,
если![]() только при условии, что
только при условии, что![]() ,
тогда линейная комбинация векторов
называетсятривиальной
линейной
комбинацией, если
,
тогда линейная комбинация векторов
называетсятривиальной
линейной
комбинацией, если
![]() ,
и существует хотя бы один
,
и существует хотя бы один![]() ,
то
,
то![]() –нетривиальная
линейная
комбинация.
–нетривиальная
линейная
комбинация.
Определение.
Если существуют такие
![]() ,
что
,
что![]() – нетривиальная линейная комбинация,
то говорят, что
– нетривиальная линейная комбинация,
то говорят, что![]() -линейно
зависимы.
В противном случае, т.е. если
-линейно
зависимы.
В противном случае, т.е. если
![]() – тривиальная линейная комбинация, то
– тривиальная линейная комбинация, то![]() –линейно
независимы.
–линейно
независимы.
Теорема.
Векторы
![]() линейно зависимы тогда и только тогда,
когда один из них является линейной
комбинацией остальных.
линейно зависимы тогда и только тогда,
когда один из них является линейной
комбинацией остальных.
Доказательство.
Необходимость.
Докажем, что если векторы
![]() линейно зависимы, то один из них является
линейной комбинацией остальных.
Поскольку векторы линейно зависимы,
то, согласно определению, существует
линейно зависимы, то один из них является
линейной комбинацией остальных.
Поскольку векторы линейно зависимы,
то, согласно определению, существует![]() ,
при котором
,
при котором![]() .
.
Пусть
![]() ,
тогда
,
тогда![]() .
Т.е. вектор
.
Т.е. вектор![]() является линейной комбинацией остальных.
является линейной комбинацией остальных.
Достаточность.
Докажем, что если один из векторов
![]() является линейной комбинацией остальных,
то векторы линейно зависимы. Пусть
является линейной комбинацией остальных,
то векторы линейно зависимы. Пусть![]() – линейная комбинация остальных
векторов, тогда
– линейная комбинация остальных
векторов, тогда![]() – линейно зависимы, поскольку
– линейно зависимы, поскольку![]() при том, что
при том, что![]() .
.
Теорема.
1.
Если хотя бы один из векторов
![]() ,
является нулевым, то эти векторы линейно
зависимы.
,
является нулевым, то эти векторы линейно
зависимы.
2. Любые два коллинеарных вектора линейно зависимы, и наоборот, два линейно зависимых вектора коллинеарные.
3. Каждые три компланарных вектора линейно зависимы, и наоборот, три линейно зависимых вектора компланарны.
4. Каждые четыре вектора линейно зависимы.
Доказательство. (Приведем доказательство 1–го и 2–го утверждений теоремы, остальные доказываются аналогично).
1. Поскольку среди векторов есть нулевой, значит, в их линейной комбинации перед нулевым вектором может стоять любой ненулевой элемент, а перед остальными векторами будут стоять нулевые элементы, это и означает линейную зависимость векторов.
2.
Докажем, что если два вектора
![]() коллинеарны, то они линейно зависимы.
Если хотя бы один из векторов
коллинеарны, то они линейно зависимы.
Если хотя бы один из векторов![]() нулевой, то они линейно зависимы в силу
предыдущего утверждения теоремы.
нулевой, то они линейно зависимы в силу
предыдущего утверждения теоремы.
Если
оба вектора ненулевые, то из свойства
коллинеарности векторов
![]() следует, что существует действительное
число
следует, что существует действительное
число![]() такое, что
такое, что![]() или
или![]() ,
поскольку
,
поскольку![]() и
и![]() отличны от нуля
отличны от нуля![]() и
и![]() линейно зависимы.
линейно зависимы.
Докажем
теперь, что два линейно зависимых вектора
-
![]() и
и![]() коллинеарны. Поскольку
коллинеарны. Поскольку![]() и
и![]() линейно зависимы, следовательно, по
определению, существуют действительные
числа
линейно зависимы, следовательно, по
определению, существуют действительные
числа![]() и
и![]() ,
хотя бы одно из них отлично от нуля,
такие, что
,
хотя бы одно из них отлично от нуля,
такие, что![]() ,
пусть
,
пусть![]() ,
тогда
,
тогда![]() ,
пусть
,
пусть![]() ,
имеем
,
имеем![]() ,
согласно свойству произведения вектора
на число, это и означает коллинеарность
векторов
,
согласно свойству произведения вектора
на число, это и означает коллинеарность
векторов![]() и
и![]() .
.
Базис.
Определение. Базисом на прямой называется любой ненулевой вектор лежащий на этой прямой или коллинеарный с ней.
Определение. Базисом на плоскости называются два неколлинеарных вектора лежащих на этой плоскости или параллельных ей, взятые в определенном порядке.
Определение. Базисом в пространстве называют три некомпланарных вектора, взятых в определенном порядке.
Определение.
Говорят, что три линейно независимых
вектора
![]() образуютбазис
в пространстве
образуютбазис
в пространстве
![]() ,
если каждый вектор этого пространства
можно представить как линейную комбинацию
этих векторов, т.е.
,
если каждый вектор этого пространства
можно представить как линейную комбинацию
этих векторов, т.е.![]() .
Числа
.
Числа![]() называются координатами вектора
называются координатами вектора![]() в базисе
в базисе![]() и вектор
и вектор![]() обычно записывают как
обычно записывают как![]() .
.
Выражение
![]() называется линейной комбинацией вектора
или разложением по базису.
называется линейной комбинацией вектора
или разложением по базису.
Запись
![]() называется координатной формой записи
вектора.
называется координатной формой записи
вектора.
Равные векторы в одном базисе имеют равные компоненты.
При
умножении вектора на число каждая его
координата умножается на это число,
т.е. если
![]() ,
то
,
то![]() =
=![]() .
.
При
сложении двух векторов их координаты,
стоящие перед соответствующими базисными
векторами, складываются, т.е.
![]() =
=![]() .
.
Утверждение. Любые три некомпланарных вектора, взятые в определенном порядке, образуют базис пространства.
Любые два неколлинеарных вектора на плоскости, взятые в определенном порядке, образуют базис на этой плоскости.
Любой ненулевой вектор, лежащий на прямой, образует базис на этой прямой.
Теорема.
Каждый вектор, параллельный какой-либо прямой, может быть разложен по базису на этой прямой.
Каждый вектор, параллельный какой-либо плоскости, может быть разложен по базису на этой плоскости.
Каждый вектор может быть разложен по базису в пространстве.
Компоненты вектора в каждом случае определяются однозначно.
Доказательство.
1.
Поскольку вектор, параллельный прямой,
и вектор, лежащий на прямой, ненулевые,
существует число α такое, что
![]() положим,
что
положим,
что![]() .
.
2.
![]() ,
вектор
,
вектор![]() является диагональю параллелограмма,
построенного на векторах
является диагональю параллелограмма,
построенного на векторах![]() .
.
3.
![]() ,
вектор
,
вектор![]() является диагональю параллелепипеда,
построенного на векторах
является диагональю параллелепипеда,
построенного на векторах![]() .
.
4.
Доказательство единственности разложения
вектора по определенному базису будем
вести от противного.
![]()
![]()
![]() и
и![]() ,
тогда
,
тогда
![]()

![]() .
.
П
![]()
![]() – противоречие некомпланарности
векторов
– противоречие некомпланарности
векторов![]() .
.
Определение.
Аффинные
координаты в пространстве определяются
заданием базиса
![]() и некоторой точкой
и некоторой точкой![]() ,
называемой началом координат.Аффинными
координатами
точки М называются координаты вектора
,
называемой началом координат.Аффинными
координатами
точки М называются координаты вектора
![]() (относительно
базиса
(относительно
базиса![]() ).
).
Определение.
В случае декартовой прямоугольной
системы координат базисом
![]() являются векторы единичной длины,
лежащие на координатных осях и
сонаправленные с ними
являются векторы единичной длины,
лежащие на координатных осях и
сонаправленные с ними![]() ,
,![]() ,
,![]() ,
,![]() .
Векторы взаимно ортогональны
.
Векторы взаимно ортогональны![]() и их модули равны единице
и их модули равны единице![]() .
.
Т.е.
векторы
![]() являются ортонормированным базисом
декартовой системы координат. Базисные
векторы имеют координаты
являются ортонормированным базисом
декартовой системы координат. Базисные
векторы имеют координаты![]() ,
,![]() ,
,![]() .
.
Тогда
каждый вектор
![]() может, и притом единственным образом,
быть разложен по декартовому прямоугольному
базису
может, и притом единственным образом,
быть разложен по декартовому прямоугольному
базису![]() ,
т.е. существует такая тройка чисел
,
т.е. существует такая тройка чисел![]() ,
что справедливо равенство
,
что справедливо равенство![]() ,
,![]() – декартовы прямоугольные координаты,
где
– декартовы прямоугольные координаты,
где![]() ,
,![]()
![]() тогда
тогда![]() ,
,![]() ,
,![]() где
где![]() – углы между вектором
– углы между вектором![]() и осями
и осями![]() соответственно (рис. 4.5), а косинусы
называются направляющими косинусами
вектора.
соответственно (рис. 4.5), а косинусы
называются направляющими косинусами
вектора.
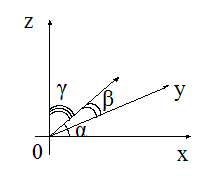
Рис. 4.5
Лекция 5
Проекция вектора и ее свойства. Деление отрезка в заданном отношении. Скалярное произведение векторов
Цель: Изучить понятие проекции и ее свойства, методику деления отрезка в данном отношении, скалярное произведение векторов, его свойства, физическое приложение.
Определение.
Проекцией
вектора
![]() на вектор
на вектор![]() ,
обозначается
,
обозначается![]() называется число, равное
называется число, равное![]() где
где![]() – угол между векторами
– угол между векторами![]() и
и![]() (рис.5.1).
(рис.5.1).
B
О
пр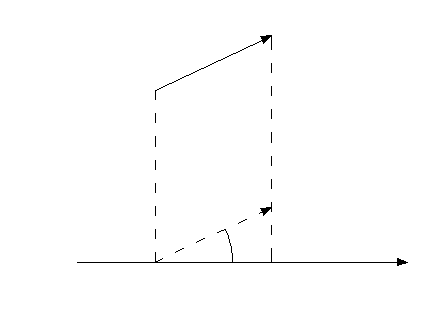
![]()
![]()
![]()
Рис. 5.1.
Свойства проекции
Проекция суммы векторов равна сумме проекций составляющих
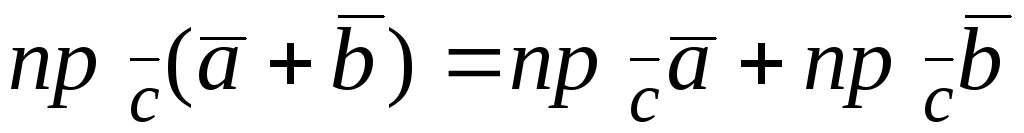 (рис. 5.2).
(рис. 5.2).
Р ис.
5.2
ис.
5.2
2)
Проекция произведения вектора на число
равна произведению числа на проекцию
данного вектора
![]() (рис. 5.3).
(рис. 5.3).
Р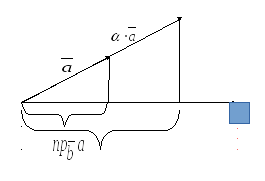 ис
5.3.
ис
5.3.
Теорема. Чтобы найти компоненты вектора, нужно из координат его конца вычесть координаты его начала, т.е.
![]() ,
где
,
где
![]() ,
,![]() (рис. 5.4).
(рис. 5.4).

Рис. 5.4
Найдем
координаты точки
![]() ,
которая делит
,
которая делит![]() в отношении
в отношении![]() (
(![]() ).
Отношение
).
Отношение![]() ,
в котором произвольная точка
,
в котором произвольная точка![]() делит отрезок
делит отрезок![]() (Рис. 5.5) удовлетворяет равенству
(Рис. 5.5) удовлетворяет равенству![]() .
.

![]()
![]()
![]()
![]()
![]()
Рис.5.5.
Пусть
![]() ,
а
,
а![]() ,
тогда разложим обе части равенства по
базису
,
тогда разложим обе части равенства по
базису![]() ,
тогда
,
тогда![]() ,
,![]() ,
,
![]()
т.к.
![]() ,
следовательно
,
следовательно
![]() .
.
![]()
![]() (5.1)
(5.1)
Когда
![]() делит
отрезок пополам, имеем:
делит
отрезок пополам, имеем:
![]()
![]()
![]() . (5.2)
. (5.2)
Скалярное произведение векторов
Определение. Скалярным произведением двух векторов называется число (скаляр) равное произведению длин этих векторов на косинус угла между ними:
![]() (5.3)
(5.3)
где
![]() -
угол между векторами
-
угол между векторами![]() .
Обозначают скалярное произведение как
.
Обозначают скалярное произведение как![]() .
.
Т.к.
![]() ,
то скалярное произведение можно вычислить
по формуле
,
то скалярное произведение можно вычислить
по формуле
![]() или
или![]() (5.4)
(5.4)
Физический
смысл скалярного произведения: работа
постоянной силы при прямолинейном
перемещении ее точки приложения.
![]() .
.
Свойства скалярного произведения
1)
![]() (коммутативность).
(коммутативность).
Непосредственно следует из коммутативности произведения чисел;
2)
![]() (дистрибутивность).
(дистрибутивность).
Для
доказательства этого свойства
воспользуемся линейным свойством
проекции и формулой, связывающей
скалярное произведение и проекцию.
Поскольку
![]() и
и
![]() ,
тогда
,
тогда
![]()
![]() =
=
![]() ;
;
Скалярный квадрат вектора равен квадрату модуля этого вектора:
![]() (5.5)
(5.5)
Выполняется
для любого вектора
![]() ,
следует из определения, поскольку угол
,
следует из определения, поскольку угол![]() между вектором
между вектором![]() и
и![]() равен нулю, тогда
равен нулю, тогда![]() ;
;
4) Скалярный множитель можно выносить за знак скалярного произведения
![]()
где
![]() -
произвольное действительное число.
-
произвольное действительное число.
Доказывается
по аналогии со свойством 2. Поскольку
![]() и
и
![]() ,
тогда
,
тогда
![]() ;
;
5) Скалярное произведение равно нулю тогда и только тогда, когда их скалярное произведение равно нулю.
![]() (5.6)
(5.6)
Доказательство.
Докажем,
что если векторы ортогональны, то их
скалярное произведение равно нулю.
Действительно, если
![]() и
и![]() ортогональны, следовательно,
ортогональны, следовательно,![]() -
угол между векторами
-
угол между векторами![]() равен
равен![]() ,
тогда
,
тогда![]() ,
тогда из определения следует, что
,
тогда из определения следует, что![]() .
.
Докажем
теперь, что если скалярное произведение
векторов
![]() равно нулю, то они ортогональны. Пусть
оба вектора ненулевые, (т.к. в противоположном
случае доказательство тривиально,
поскольку нулевой вектор не имеет
определенного направления и его можно
считать ортогональным любому вектору).
Тогда
равно нулю, то они ортогональны. Пусть
оба вектора ненулевые, (т.к. в противоположном
случае доказательство тривиально,
поскольку нулевой вектор не имеет
определенного направления и его можно
считать ортогональным любому вектору).
Тогда![]() и
и![]() ,
поэтому
,
поэтому![]() только в том случае, если
только в том случае, если![]() ,
т.е. векторы
,
т.е. векторы![]() должны быть ортогональны.
должны быть ортогональны.
6)
векторы ортонормированного базиса
декартовой прямоугольной системы
координат
![]() удовлетворяют соотношениям:
удовлетворяют соотношениям:
![]() ,
,
![]() т.к. векторы попарно ортогональны
т.к. векторы попарно ортогональны
![]() .
.
Если
базисные векторы
![]() ортогональны, то для каждого вектора
ортогональны, то для каждого вектора
![]() координаты в данном базисе будут равны:
координаты в данном базисе будут равны:![]()
![]()
![]() ,
поскольку
,
поскольку
![]() –
ортонормированный базис, тогда
–
ортонормированный базис, тогда
![]() .
.
Геометрический
смысл скалярного произведения: с
помощью скалярного произведения можно
вычислить проекцию вектора
![]() на вектор
на вектор![]() ,
и косинус угла между векторами:
,
и косинус угла между векторами:
![]()
![]() (5.7)
(5.7)
![]()
![]() (5.8)
(5.8)
Теорема.
Если базис ортонормированный и
![]() ,
,![]() ,
то
,
то
![]() (5.9)
(5.9)
где
![]()
![]() –
координаты векторов в ортонормированном
базисе.
–
координаты векторов в ортонормированном
базисе.
Доказательство.
Поскольку
![]() и
и![]() ,
тогда найдем скалярное произведение
векторов используя свойства дистрибутивности
и ассоциативности:
,
тогда найдем скалярное произведение
векторов используя свойства дистрибутивности
и ассоциативности:
![]()
![]()
![]() =
=
=
![]()
![]()
![]()
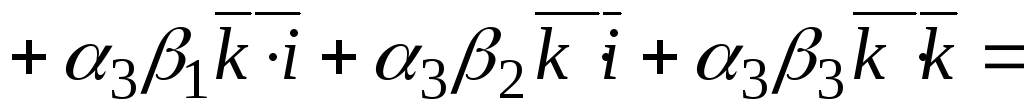
![]() .
.
Следствие.
Необходимым
и достаточным условием ортогональности
векторов
![]() и
и![]() является условие
является условие![]() .
.
Следствие.
Длина
(модуль) вектора
![]() равна
равна![]() .
.
Следствие.
![]() ,
где
,
где![]() -
угол между векторами
-
угол между векторами![]() .
.
Следствие.
Если
![]() ,
тогда:
,
тогда:
![]() .
.
Лекция 6
Векторное произведение векторов, смешанное произведение векторов, основные свойства. Условия ортогональности, коллинеарности, компланарности векторов.
Цель: Изучить векторное и смешанное произведение векторов, их свойства, методы вычисления, условия ортогональности, компланарности и коллинеарности векторов.
Определение.
Векторным
произведением
двух векторов
![]() ,
обозначают
,
обозначают![]() называется вектор
называется вектор![]() удовлетворяющий трем условиям:
удовлетворяющий трем условиям:
1) Модуль вектора равен площади параллелограмма, построенного на этих векторах
![]() (6.1)
(6.1)
2)
Вектор ортогонален перемножаемым
векторам:
![]() т.е. ортогонален плоскости построенного
на этих векторах параллелограмма
т.е. ортогонален плоскости построенного
на этих векторах параллелограмма
3)
![]() составляют правую тройку векторов
(рис.6.1).
составляют правую тройку векторов
(рис.6.1).

Рис. 6.1
Свойства векторного произведения
1)
![]() (антикоммутативность)
(антикоммутативность)
Свойство следует из перемены ориентации векторов;
2)
Скалярный множитель можно вынести за
скобку
![]() ;
;
3)
![]() (дистрибутивность);
(дистрибутивность);
4) Векторный квадрат равен нуль-вектору:
![]() (6.2)
(6.2)
Свойство непосредственно вытекает из определения векторного произведения
Теорема.
Чтобы
векторы
![]() и
и![]() были коллинеарны, необходимо и достаточно,
чтобы их векторное произведение равнялось
нулю.
были коллинеарны, необходимо и достаточно,
чтобы их векторное произведение равнялось
нулю.
![]() (6.3)
(6.3)
Доказательство.
Докажем,
что если
векторы
коллинеарны, то их векторное произведение
равно нулю. Действительно, т.к. векторы
![]() и
и![]() коллинеарны, значит, угол
коллинеарны, значит, угол![]() между ними составляет
между ними составляет![]() либо
либо![]() .
Тогда
.
Тогда![]() ,
т.е. длина вектора, полученного в
результате перемножения коллинеарных
векторов, равна нулю, это возможно только
у нулевого вектора.
,
т.е. длина вектора, полученного в
результате перемножения коллинеарных
векторов, равна нулю, это возможно только
у нулевого вектора.
Докажем
теперь, что если векторное произведение
равно нулю, то векторы коллинеарны.
Пусть оба вектора
![]() и
и![]() ненулевые (в противном случае доказательство
тривиально), тогда
ненулевые (в противном случае доказательство
тривиально), тогда![]() и
и![]() ,
поэтому
,
поэтому![]() только в том случае, если
только в том случае, если![]() ,
т.е. векторы
,
т.е. векторы![]() должны быть коллинеарны.
должны быть коллинеарны.
Теорема.
В ортонормированном базисе декартовой
прямоугольной системы координат
![]() компоненты векторного произведения
могут быть вычислены по формуле:
компоненты векторного произведения
могут быть вычислены по формуле:
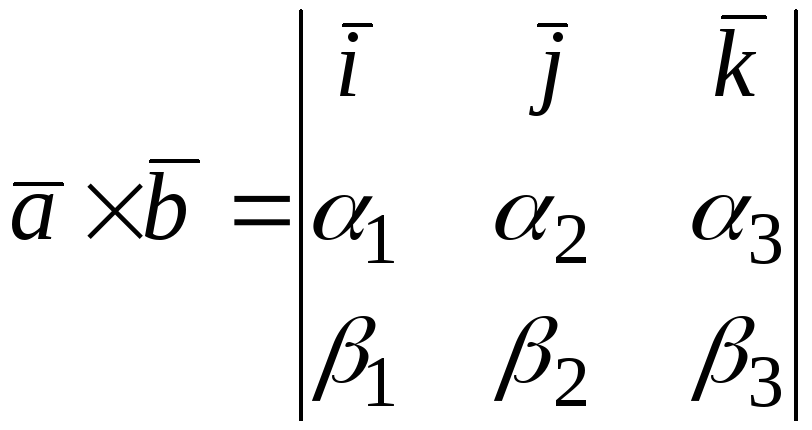 (6.4)
(6.4)
где
![]() ,
,![]() .
.
Доказательство.
Поскольку
![]() и
и
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
тогда
![]()
![]()
![]()
![]()
=(учитывая выше записанные равенства, упрощаем полученное выражение)
![]()
![]()
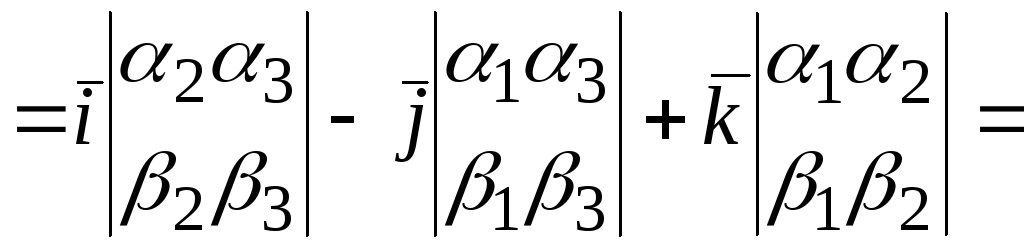
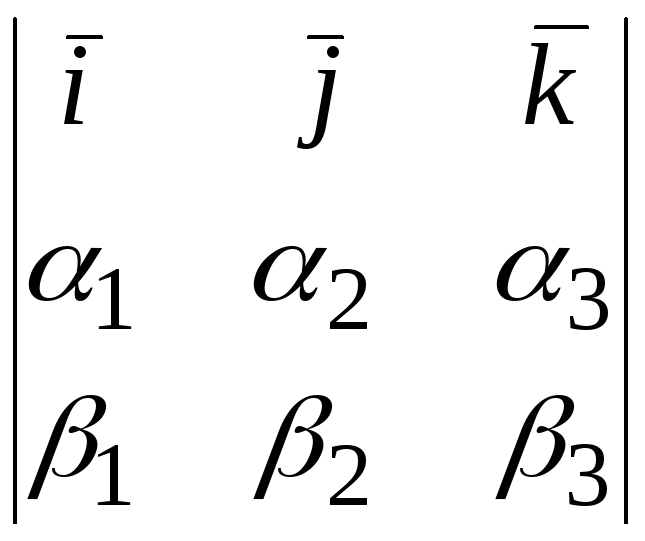 .
.
Вместо
![]() можно взять любой ортонормированный
базис.
можно взять любой ортонормированный
базис.
Теорема (о коллинеарных векторах). Если два вектора коллинеарны, то их координаты пропорциональны:
![]() (6.5)
(6.5)
Доказательство.
Пусть
![]() и
и![]() ,
т.к. вектор
,
т.к. вектор
![]() коллинеарен
коллинеарен
![]() ,
тогда
,
тогда
![]() ,согласно
предыдущей теореме, выполняются
равенства
,согласно
предыдущей теореме, выполняются
равенства
![]()
![]()
![]()
![]() ,
получаем пропорцию
,
получаем пропорцию
![]() .
.
Геометрический смысл векторного произведения
Поскольку
![]() ,
то значение длины векторного произведения
совпадает с значением площади
параллелограмма, построенного на
векторах
,
то значение длины векторного произведения
совпадает с значением площади
параллелограмма, построенного на
векторах
![]() как на сторонах.
как на сторонах.![]()
![]() – площадь параллелограмма, построенного
на векторах
– площадь параллелограмма, построенного
на векторах![]() как на сторонах.
как на сторонах.
![]() –площадь
треугольника, построенного на векторах
–площадь
треугольника, построенного на векторах
![]() .
.
Пример.
Найти площадь треугольника![]()
![]() построенного на векторах
построенного на векторах![]() и
и![]() ,
если
,
если![]() ;
;![]() ;
;![]() .Решение.
.Решение.![]()
![]()
![]()
![]()
![]()
Смешанное произведение
Определение.
Под смешанным
произведением
векторов
![]() подразумевают число обозначаемое
подразумевают число обозначаемое![]() и получающееся в результате скалярного
произведения вектора
и получающееся в результате скалярного
произведения вектора![]() на векторное произведение
на векторное произведение![]() .
.
Теорема
(геометрический
смысл смешанного произведения).
Смешанное произведение трех некомпланарных
векторов
![]() по модулю равно объему параллелепипеда,
построенного на сомножителях.
по модулю равно объему параллелепипеда,
построенного на сомножителях.
![]()
![]() ,
причем
,
причем
![]() - имеет знак «
- имеет знак «![]() »
если
»
если![]() образуют правую тройка и «
образуют правую тройка и «![]() »
если
»
если![]() -
левая тройка.
-
левая тройка.
Доказательство.
![]() –объем
параллелепипеда, где
–объем
параллелепипеда, где
![]()
![]() –
площадь основания,
–
площадь основания,
![]() –
высота параллелепипеда,
–
высота параллелепипеда,
![]() -
угол между вектором
-
угол между вектором![]() и вектором
и вектором![]() (рис.
6.2), тогда
(рис.
6.2), тогда
![]() .
.

Рис. 6.2
Следствие.
![]()
![]() –
объем пирамиды.
–
объем пирамиды.
Свойства смешанного произведения
1)
![]() ,
данное свойство позволяет записывать
смешанное произведение в виде
,
данное свойство позволяет записывать
смешанное произведение в виде![]() .
Действительно, из коммутативности
скалярного произведения следует, что
.
Действительно, из коммутативности
скалярного произведения следует, что![]() ,
докажем, что
,
докажем, что![]() ,
равенство очевидно, поскольку и справа,
и слева стоит объем параллелепипеда,
построенного на одних и тех же векторах,
знаки совпадают, поскольку векторы
,
равенство очевидно, поскольку и справа,
и слева стоит объем параллелепипеда,
построенного на одних и тех же векторах,
знаки совпадают, поскольку векторы![]() -
имеют одинаковую ориентацию;
-
имеют одинаковую ориентацию;
2) При перестановки местами двух соседних множителей, смешанное произведение меняет знак на противоположный
![]() .
.
Данное свойство следует из антикоммутативности векторного произведения.
3)
![]() .
Действительно, т.к. выполняется первое
свойство, тогда
.
Действительно, т.к. выполняется первое
свойство, тогда
![]() ,
согласно линейным свойствам скалярного
произведения, получаем равенство.
,
согласно линейным свойствам скалярного
произведения, получаем равенство.
Теорема
(смешанное
произведение векторов в ортонормированном
базисе).
В ортонормированном базисе
![]() смешанное произведение может быть
вычислено по формуле:
смешанное произведение может быть
вычислено по формуле:
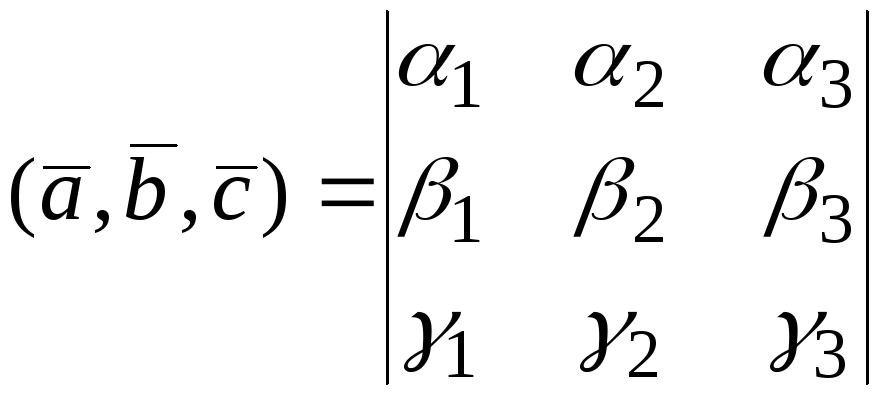 (6.6)
(6.6)
Доказательство.
Действительно, смешанное произведение
равно скалярному произведению векторов
![]() и
и![]() ,
поскольку координаты
,
поскольку координаты![]()
![]() ,
для скалярного произведения векторов
в координатах получим
,
для скалярного произведения векторов
в координатах получим![]()
![]() =
=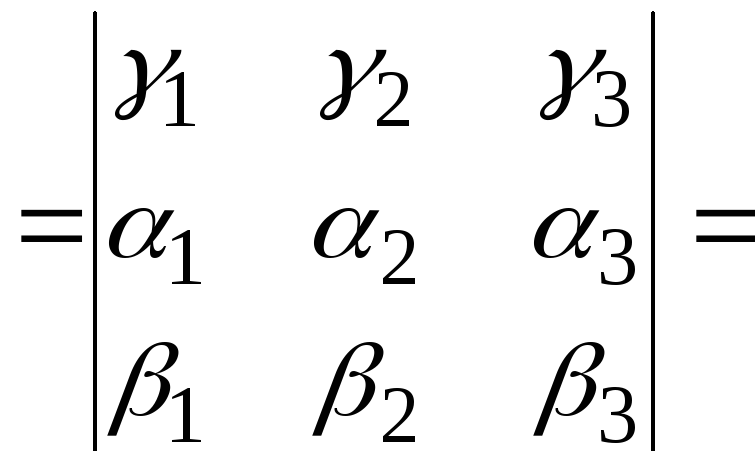 (т.к.
четное число перестановок не меняет
знак определителя) =
(т.к.
четное число перестановок не меняет
знак определителя) =
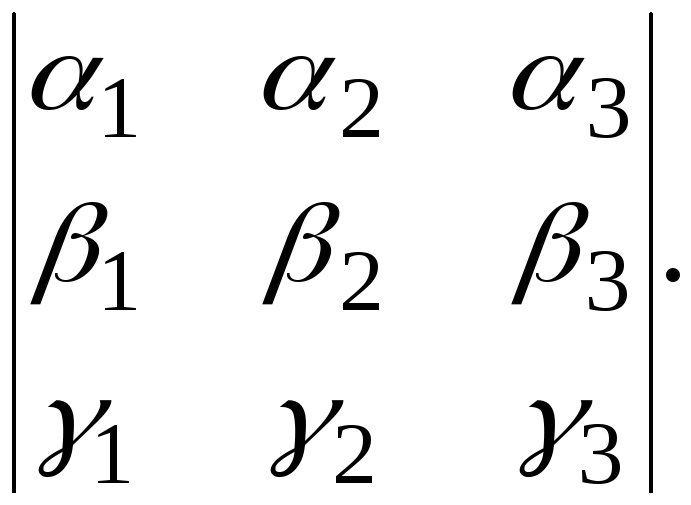
Теорема
(о
компланарных векторах). Для
того, чтобы
![]() были компланарны, необходимо и достаточно,
чтобы их смешанное произведение равнялось
нулю, т.е. выполняется равенство:
были компланарны, необходимо и достаточно,
чтобы их смешанное произведение равнялось
нулю, т.е. выполняется равенство:
![]()
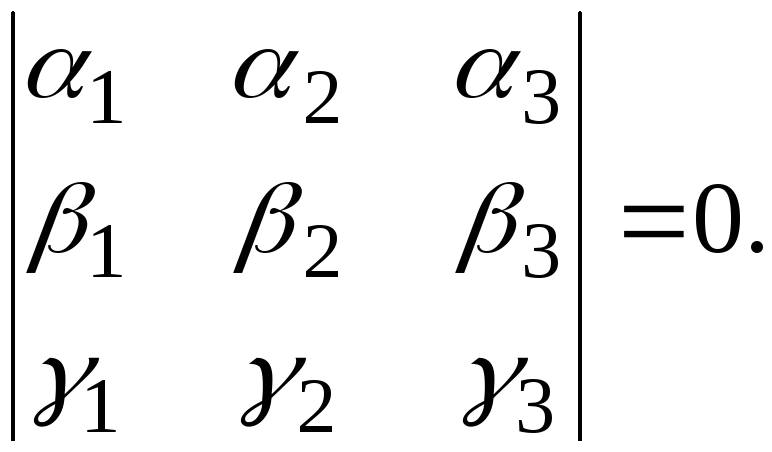 (6.7)
(6.7)
В самом деле, если векторы компланарны, то они по определению лежат в одной плоскости или в параллельных плоскостях, следовательно, объем параллелепипеда, построенного на этих векторах, будет равен нулю, учитывая запись смешанного произведения в координатной форме, получаем требуемое равенство. В обратную сторону доказательство аналогично.
Следствие.
Смешанное произведение трех векторов
два из которых совпадают, равно нулю,
например,
![]() .
.
Действительно, поскольку такие векторы заведомо компланарны, их сшешанное произведение будет равно нулю.
Определение.
Вектор
![]() –
называетсядвойным
векторным произведением.
–
называетсядвойным
векторным произведением.
