
Свойства определителя
Все свойства определителя следуют из определения определителя и свойств конечных сумм, приводятся без общих доказательств с демонстрацией на примере определителей 2-го и 3-го порядков.
Свойство 1. Равноправность строк и столбцов. Определитель не меняет своего значения при замене всех его строк соответствующими столбцами
![]() (11.4)
(11.4)
Т.е.
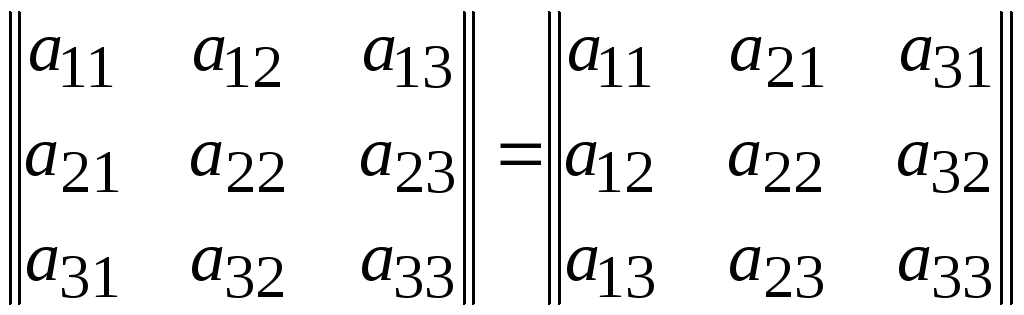 .
.
Для доказательства этого свойства достаточно вычислить определители в левой и правой частях равенства и убедиться в равенстве полученных при этом членов.
В связи с этим свойством в дальнейшем вместо слов «строка» или «столбец» будем говорить просто «ряд», подразумевая их равноправность.
Свойство 2. При перестановке двух параллельных рядов определителя его модуль сохраняет прежнее значение, а знак меняется на противоположный
Пример:
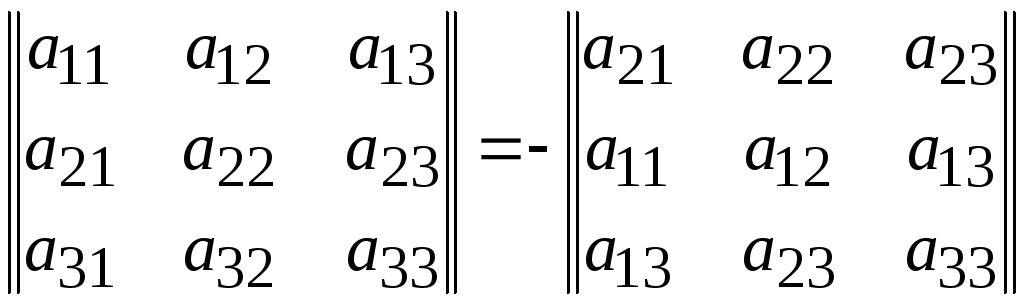 .
.
Для доказательства этого свойства достаточно вычислить по правилу треугольника определители, стоящие в правой и левой частях равенства.
Следствие 1: Определитель с двумя одинаковыми рядами равен нулю.
Действительно,
при перестановке двух одинаковых рядов
абсолютное значение определителя не
изменится, а, с другой стороны, в силу
свойства 2 изменит знак на противоположный,
т.е.
![]() ,
значит
,
значит![]() ,
следовательно,
,
следовательно,![]() .
.
Следствие 2. Сумма произведений элементов какого либо ряда на алгебраические дополнения параллельного ряда равна нулю.
Действительно, все такие разложения представляют из себя определители, содержащие два одинаковых ряда:
![]()
![]()
![]()
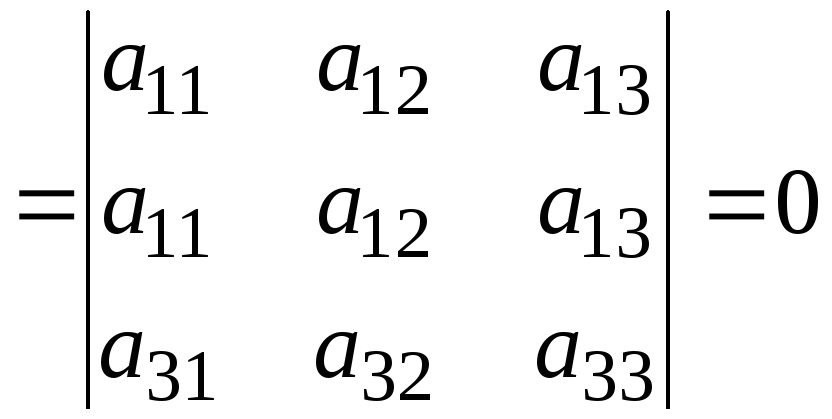
Свойство 3. Общий множитель элементов какого либо ряда можно выносить за знак определителя.
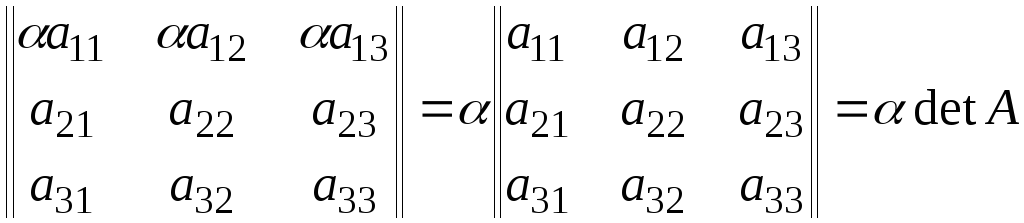 .
.
Действительно,
поскольку определитель можно вычислить,
раскладывая его по элементам строки
(столбца), вычислим определитель,
раскладывая его по элементам строки,
умноженной на число
![]() ,
тогда каждое слагаемое будет содержать
множитель
,
тогда каждое слагаемое будет содержать
множитель![]() ,
который может быть вынесен за скобку.
,
который может быть вынесен за скобку.
Следствие 1. Если все элементы какого-либо ряда равны нулю, то определитель равен нулю.
Следствие 2. Если все элементы какого-либо ряда определителя пропорциональны соответствующим элементам параллельного ряда, то определитель равен нулю.
Действительно,
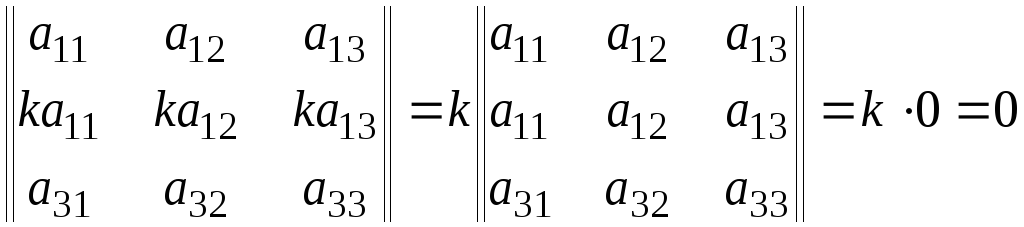
Свойство
4.
Линейное свойство определителя. Если
в определителе
![]() -го
порядка некоторая
-го
порядка некоторая![]() -ая
строка представляет собой сумму двух
слагаемых, то определитель может быть
представлен в виде суммы двух определителей.
Первый определитель будет иметь в
-ая
строка представляет собой сумму двух
слагаемых, то определитель может быть
представлен в виде суммы двух определителей.
Первый определитель будет иметь в![]() -ой
строке первые из упомянутых слагаемых
, элементы в остальных строках будут
такими же, как и в исходном определителе,
а второй определитель в
-ой
строке первые из упомянутых слагаемых
, элементы в остальных строках будут
такими же, как и в исходном определителе,
а второй определитель в![]() -ой
строке будет иметь вторые из упомянутых
слагаемых, а остальные строки будут
совпадать с исходным определителем,
т.е.
-ой
строке будет иметь вторые из упомянутых
слагаемых, а остальные строки будут
совпадать с исходным определителем,
т.е.
![]() .
.
Это
свойство следует из определения
определителя, если разложить его по
элементам
![]() -ой
строки, а затем воспользоваться
распределительным законом суммы.
-ой
строки, а затем воспользоваться
распределительным законом суммы.
Определение. Элементарными преобразованиями матрицы называются следующие преобразования:
1) умножение строки (столбца) на число отличное от нуля;
2) прибавление к одной строке (столбцу) другой строки (столбца);
3) перестановка строк (столбцов).
Свойство
5.
Если к элементам некоторой строки
(столбца) определителя прибавить
соответствующие элементы другой строки
(столбца), умноженные на произвольный
множитель
![]() ,
то величина определителя не изменится.
,
то величина определителя не изменится.
Свойство 6. Определитель треугольной матрицы равен произведению диагональных элементов.
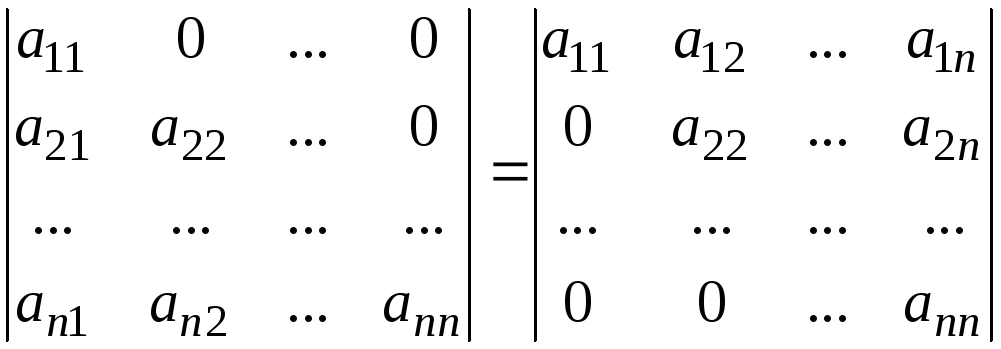 =
=![]() .
.
нижний треугольный верхний треугольный
определитель определитель
Определение.
Минором
![]() -ого
порядка
матрицы
-ого
порядка
матрицы
![]() называется детерминант матрицы порядка
называется детерминант матрицы порядка![]() ,
образованный элементами, стоящими на
пересечении выбранных
,
образованный элементами, стоящими на
пересечении выбранных![]() строк и столбцов. Каждая матрица имеет
столько миноров данного порядка,
сколькими способами можно выбрать
номера строк и столбцов. Если матрица
строк и столбцов. Каждая матрица имеет
столько миноров данного порядка,
сколькими способами можно выбрать
номера строк и столбцов. Если матрица![]() квадратная, то каждому минору
квадратная, то каждому минору
![]() –ого
порядка
сопоставляется дополнительный
минор,
который по определению есть определитель
матрицы порядка (
–ого
порядка
сопоставляется дополнительный
минор,
который по определению есть определитель
матрицы порядка (![]() ),
составленный из элементов, оставшихся
после вычеркивания
),
составленный из элементов, оставшихся
после вычеркивания
![]() строк
и столбцов.
строк
и столбцов.
Лекция 12
Линейные комбинации строк и столбцов. Базисные строки и столбцы. Линейная независимость. Ранг матрицы. Вычисление ранга.
Цель: изучить понятие линейной комбинации и линейной независимости строк и столбцов матрицы, методы вычисления ранга и определения базисного минора.
В теме «матрицы и действия над ними» мы ввели понятия матрицы строки и матрицы столбца,
Определение.
Столбец
![]() назовем линейной комбинацией столбцов
назовем линейной комбинацией столбцов![]() одинаковой высоты, если при некоторых
числах
одинаковой высоты, если при некоторых
числах![]() имеет место равенство:
имеет место равенство:
![]() (12.1)
(12.1)
Или в развернутом виде:
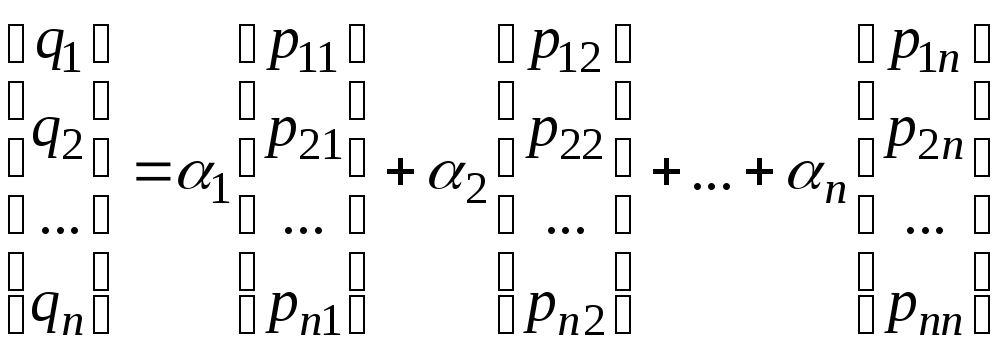 .
.
В силу определения умножения матриц на число и операции сложения последнее равенство можно представить в виде системы равенств, составленных для каждого элемента:
![]() ;
;
![]() ;
;
…
![]() .
.
По
аналогии с линейной комбинацией введем
понятие линейной независимости строк
и столбцов матрицы. Пусть
![]() - столбец у которого все элементы равны
нулю.
- столбец у которого все элементы равны
нулю.
Определение.
Система из
![]() столбцов
столбцов![]() называется линейно независимой, если
из равенства
называется линейно независимой, если
из равенства![]() следует,
следует,![]() .
В противном случае, если не все
.
В противном случае, если не все![]() (
(![]() ),
система столбцов линейно зависима.
),
система столбцов линейно зависима.
Все утверждения записанные для столбцов, справедливы и для строк матрицы.
Пример: Столбцы
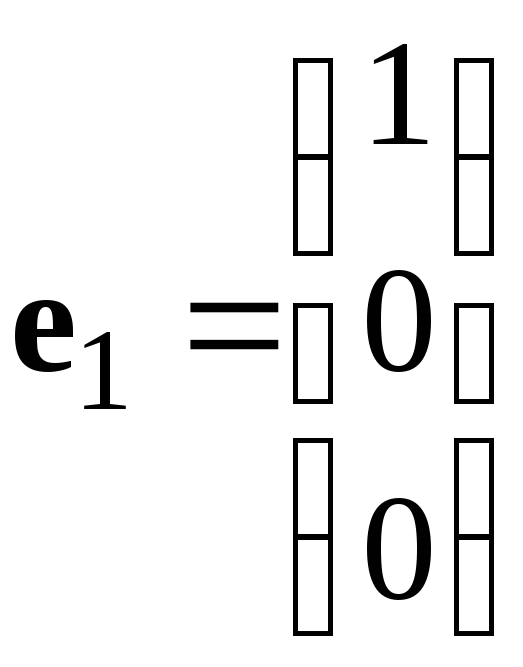 ,
,
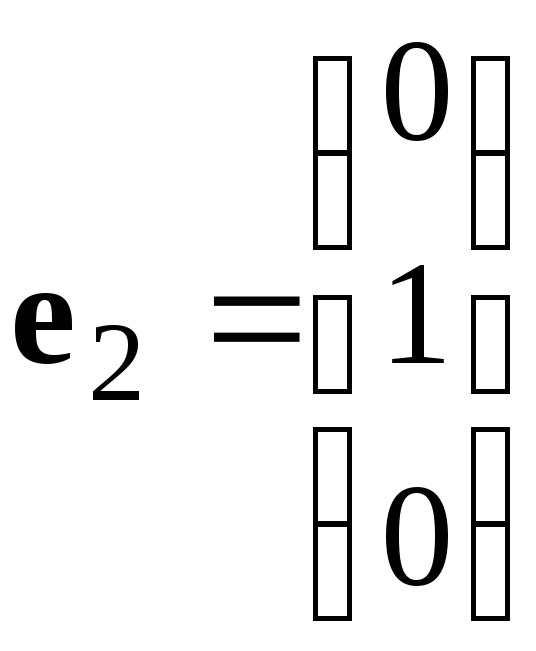 ,
,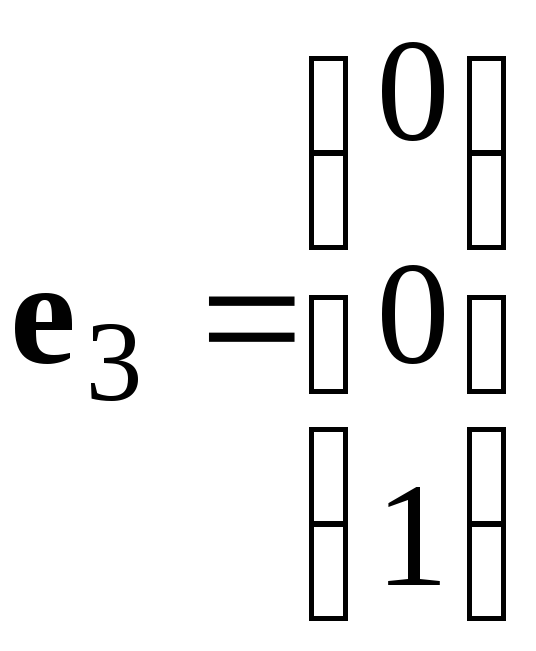
линейно независимы, т.к. их линейная комбинация
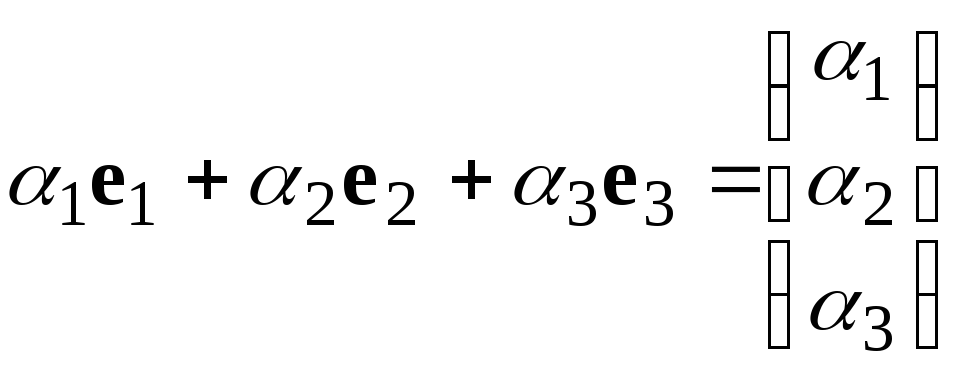
равна
нулевому столбцу, только в случае, когда
![]() ,
т.е. является тривиальной.
,
т.е. является тривиальной.
