
- •Пишкова Наталья Евгеньевна Основные методы построения графиков функций
- •1.Параллельный перенос
- •Перенос (сдвиг) вдоль оси ординат
- •1.2 Перенос вдоль оси абсцисс
- •2.Отражение
- •2.3.Построение графиков чётной и нечётной функций
- •2.4. Построение графика обратной функции
- •3. Деформация (сжатие и растяжение)
- •3.1 Сжатие (растяжение) графика вдоль оси ординат
- •3.2. Сжатие (растяжение) графика вдоль оси абсцисс
- •4. Комбинация переноса, отражения и деформации
3. Деформация (сжатие и растяжение)
3.1 Сжатие (растяжение) графика вдоль оси ординат
Рассмотрим
функцию вида y=A![]() ,
где A>0.
Нетрудно заметить, что при равных
значениях аргумента ординаты графика
этой функции будут в A
раз больше ординат графика функции
y=f(x)
при A>1
или в
,
где A>0.
Нетрудно заметить, что при равных
значениях аргумента ординаты графика
этой функции будут в A
раз больше ординат графика функции
y=f(x)
при A>1
или в
![]() раз меньше ординат графика функцииy=f(x)
при A<1.
Таким образом, получаем следующее
правило.
раз меньше ординат графика функцииy=f(x)
при A<1.
Таким образом, получаем следующее
правило.
Для
построения графика функции y=A![]() следует построить график функции y=f(x)
и увеличить его ординаты в A
раз при A>1
(произвести растяжение графика вдоль
оси ординат) или уменьшить его ординаты
в
следует построить график функции y=f(x)
и увеличить его ординаты в A
раз при A>1
(произвести растяжение графика вдоль
оси ординат) или уменьшить его ординаты
в
![]() раз приA<1
(произвести сжатие графика вдоль оси
ординат). Полученный график является
графиком функции y=A
раз приA<1
(произвести сжатие графика вдоль оси
ординат). Полученный график является
графиком функции y=A![]() .
.
Пример 13. Построить график функции y=2cos x.
Р е ш е н и е: Строим график функции y=cos x (рис.16 – пунктирная кривая) и растяжением этого графика вдоль оси ординат в 2 раза получаем график функции y=2cos x (сплошная кривая).
Пример
14. Построить
график функции y=![]() x2.
x2.
Р
е ш е н и е: Строим график функции y=x2
и сжатием этого графика в 3 раза вдоль
оси ординат получаем график функции
y=![]() x2
(рис.17).
x2
(рис.17).
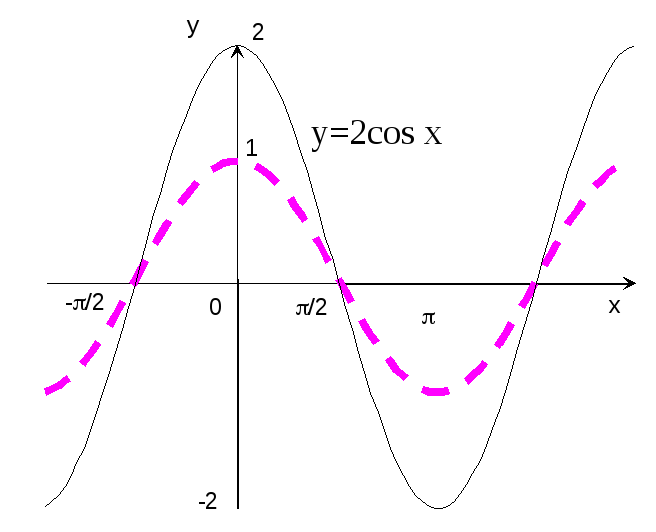
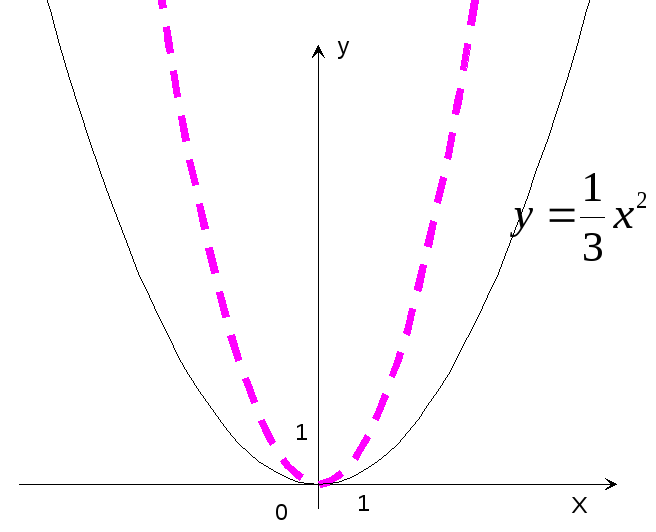
Рис.16 Рис.17
3.2. Сжатие (растяжение) графика вдоль оси абсцисс
Пусть требуется построить график функции y=f(x), где >0. Рассмотрим функцию y=f(x), которая в произвольной точке x=x1 принимает значение y1=f(x1).
Очевидно, что функция y=f(x) принимает такое же значение в точке x=x2, координата
к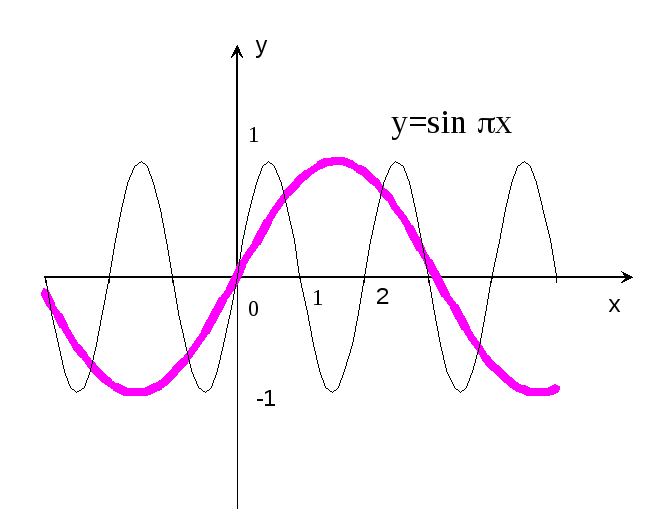 оторой
определяется равенствомx1=x2,
или x2=
оторой
определяется равенствомx1=x2,
или x2=![]() ,
причём это равенство справедливо для
совокупности всех значений x
из области определения функции.
Следовательно, график функции y=f(x)
оказывается сжатым (при >1)
или растянутым (при <1)
вдоль оси абсцисс относительно графика
функции y=f(x).
Таким образом, получаем следующее
правило.
,
причём это равенство справедливо для
совокупности всех значений x
из области определения функции.
Следовательно, график функции y=f(x)
оказывается сжатым (при >1)
или растянутым (при <1)
вдоль оси абсцисс относительно графика
функции y=f(x).
Таким образом, получаем следующее
правило.
Для
построения графика функции y=f(x)
следует построить график функции y=f(x)
и уменьшить его абсциссы в
раз при >1
(произвести сжатие графика вдоль оси
абсцисс) или увеличить его абсциссы в
![]() раз при<1
(произвести растяжение графика вдоль
оси абсцисс). Полученный график является
графиком функции y=f(x).
раз при<1
(произвести растяжение графика вдоль
оси абсцисс). Полученный график является
графиком функции y=f(x).
П
Рис. 18![]() x.
x.
Р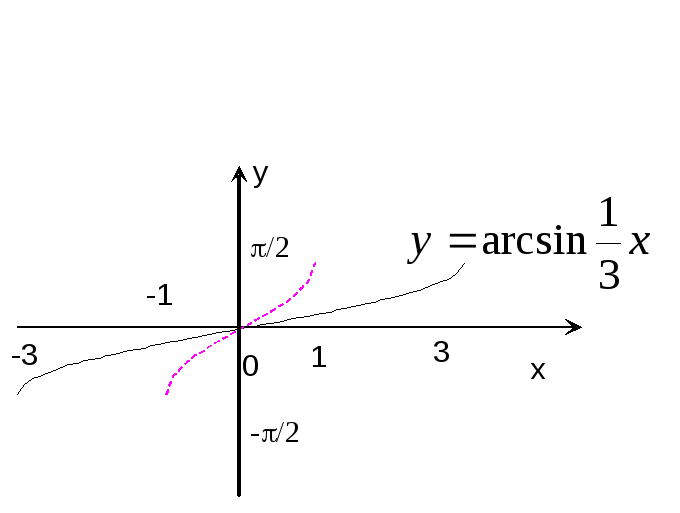 е ш е н и е: Строим график функции
е ш е н и е: Строим график функции
![]() x
(рис.18 – пунктирная кривая), и проводя
его сжатие в
раз вдоль оси абсцисс, получаем график
функции
x
(рис.18 – пунктирная кривая), и проводя
его сжатие в
раз вдоль оси абсцисс, получаем график
функции
![]() x
(сплошная кривая). Период этой функции
уже равен не 2,
а
x
(сплошная кривая). Период этой функции
уже равен не 2,
а
![]() =2.
График пересекает ось абсцисс в точкахx=0,
=2.
График пересекает ось абсцисс в точкахx=0,![]() …
.
…
.
Пример
16. Построить
график функции
![]() .
.
Р
е ш е н и е: Строим график функции
![]() и, растянув его вдоль оси абсцисс в 3
раза, получаем график функции
и, растянув его вдоль оси абсцисс в 3
раза, получаем график функции![]() .
.
4. Комбинация переноса, отражения и деформации
Рис.
19
Рассмотрим,
как с учётом изложенного следует,
например, построить
график функции вида y=Af(x+a)+b.
Запишем
исходную функцию в виде y=Af
[
( x+![]() ) ] +b
и схему поэтапного её упрощения
(последовательность преобразований):
) ] +b
и схему поэтапного её упрощения
(последовательность преобразований):
1
 .y=Af
[
( x+
.y=Af
[
( x+![]() ) ] + b
; перенос оси абсцисс на b
единиц;
) ] + b
; перенос оси абсцисс на b
единиц;
2
 .y=Af
[
( x+
.y=Af
[
( x+![]() ) ]; перенос оси ординат на
) ]; перенос оси ординат на
![]() единиц;
единиц;
3. y=Af [ x ]; отражение графика относительно оси абсцисс
( этап
выполняется только приA<0);
этап
выполняется только приA<0);
4 .y=A·
f
(x); сжатие
или растяжение графика
.y=A·
f
(x); сжатие
или растяжение графика
вдоль оси ординат;
5. y=f (x) отражение графика относительно оси ординат
( этап
выполняется только при<0);
этап
выполняется только при<0);
6 .y=f
(
x); сжатие
или растяжение вдоль оси абсцисс;
.y=f
(
x); сжатие
или растяжение вдоль оси абсцисс;
7. y=f ( x);
Проводя построение графика шаг за шагом в порядке, обратном порядку упрощения вида функции с учётом всех указанных правил, получим график исходной функции.
Пример 17. Построить
график функции y=![]() .
.
Р
 е ш е н и е: Схема построения графика :
е ш е н и е: Схема построения графика :
y
 =
=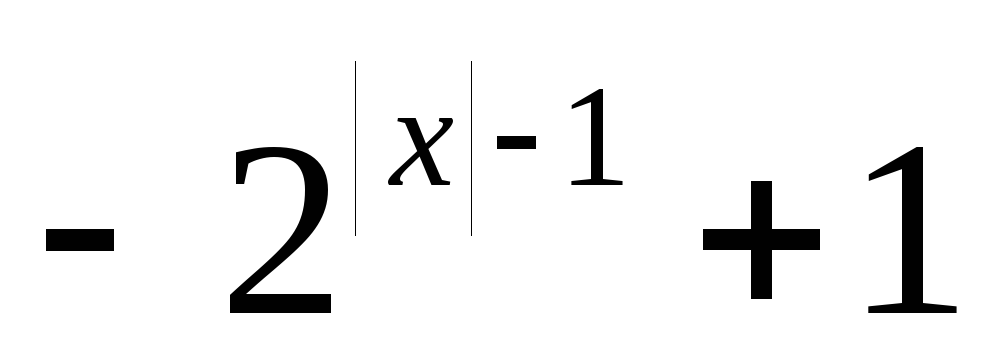
x
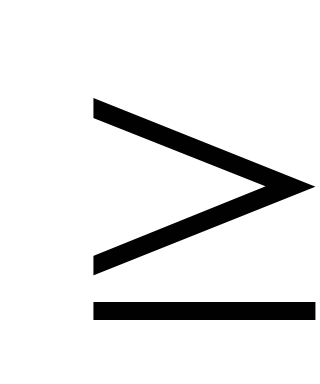 0,
y=
0,
y=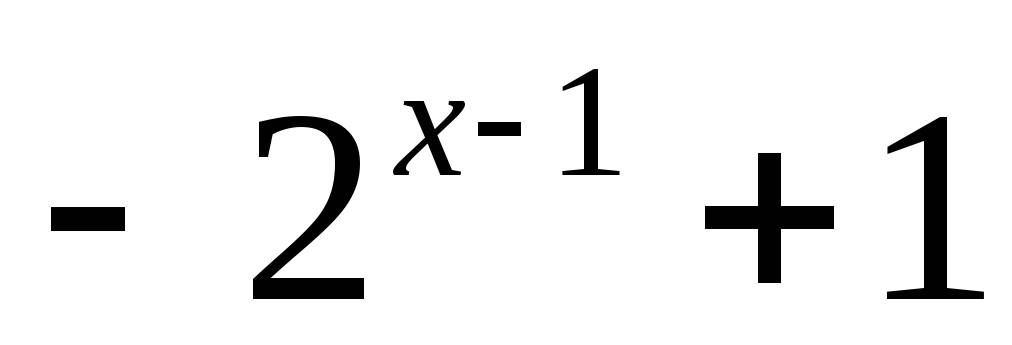 ;
;y=
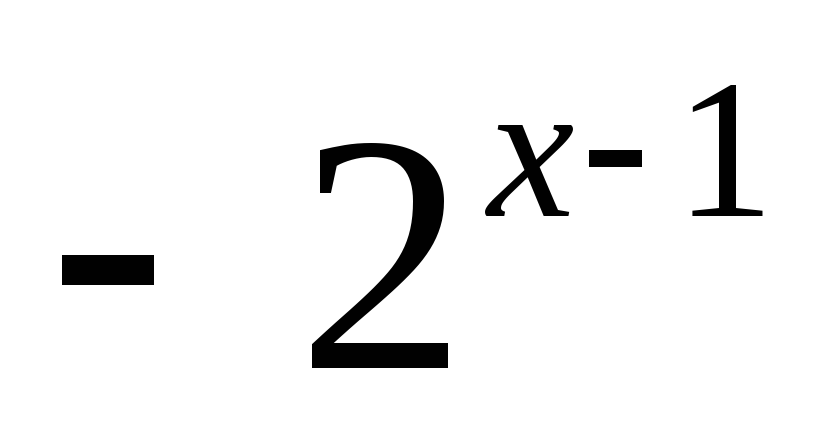 ;
;у=
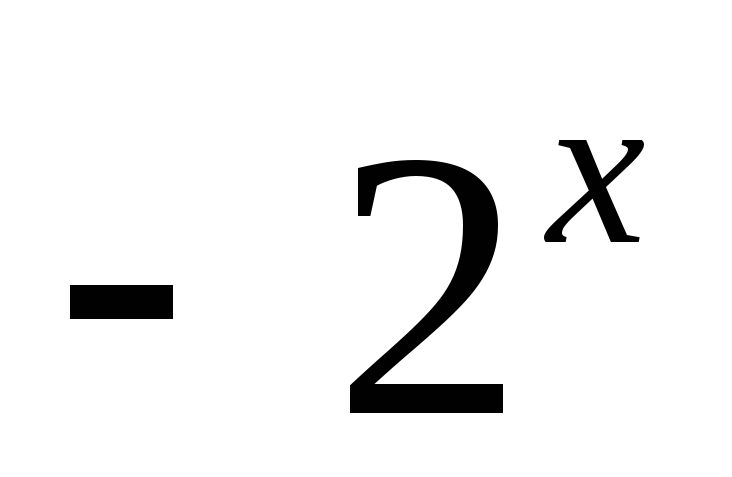 ;
;y=
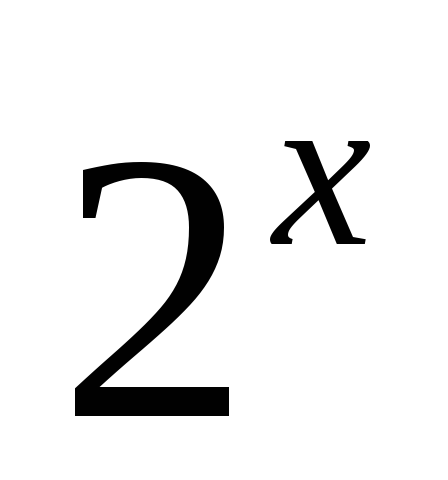 ;
;
Итак,
построение графика исходной функции
следует начинать с построения графика
функции y=![]() .
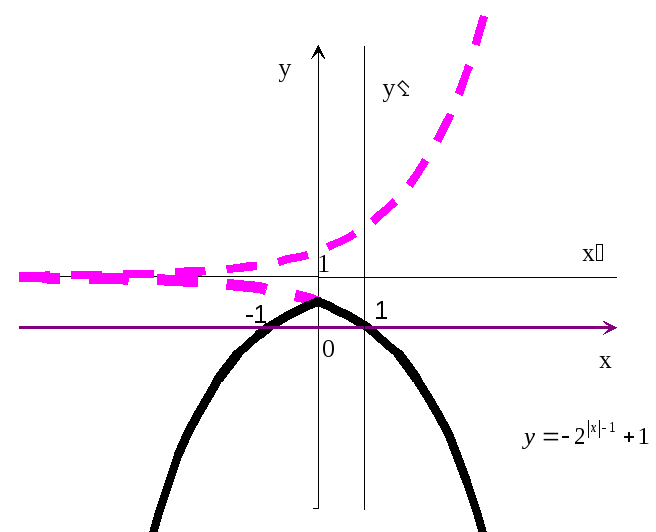
График (рис.20) пересекает ось ординат
в точке
.
График (рис.20) пересекает ось ординат
в точке![]() (из условияx=0),
а ось абсцисс в точках x=1
(из условия y=0,
т.е.
(из условияx=0),
а ось абсцисс в точках x=1
(из условия y=0,
т.е.![]() =0).
=0).
 В
заключении отметим, что порядок упрощения
целесообразно проводить в следующей
последовательности.
В
заключении отметим, что порядок упрощения
целесообразно проводить в следующей
последовательности.
Использование чётности или нечётности функции.
Перенос осей.
Отражение и деформация.
Построение же графика, как обычно, выполняется в обратной последовательности.
Рис.20
Задание для самостоятельного выполнения
Ниже приводятся тексты заданий для самостоятельного выполнения. Вам необходимо построить графики функций, оформить работу отдельно от решений по другим предметам и выслать в адрес Хабаровской краевой заочной физико-математической школы.
М.11.2.1 С помощью элементарных преобразований постройте графики следующих функций:
y=x2-2;
y=(x+1)2;
y=sin
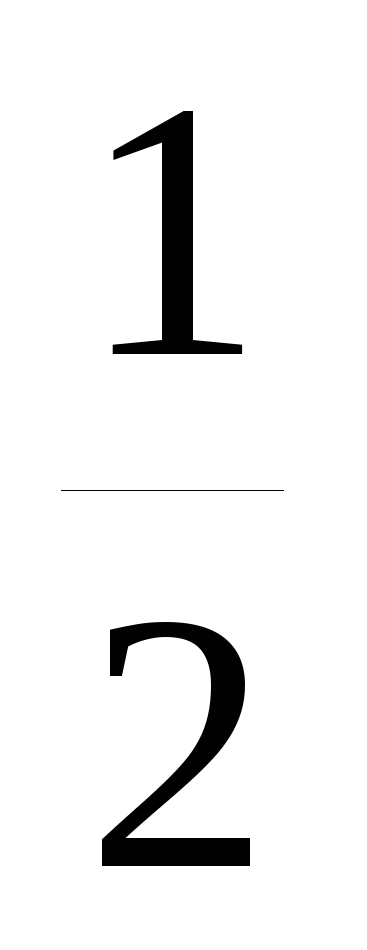 x;
x;y=- 3sin x;
y=tg
 ;
;
М.11.2.2. Написать последовательность преобразований и построить графики следующих функций:
y=
 ;
;y=(x-1)3+2;
y=ln (1-x);
y=tg(-
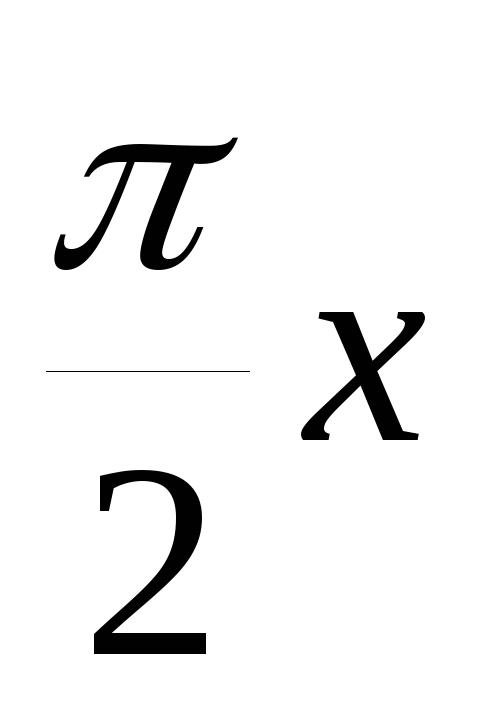 );
);y=
 cos(2x-1)-2.
cos(2x-1)-2.
Хабаровская краевая заочная физико-математическая школа
