7-8

7. Ангармонизм колебания решетки. Тепловое расширение.

V – потенциальная энергия. V=V, - совокупность смещения всех атомов. , a–постоянная решетки, расстояние до соседней ячейки. VПервые два слагаемых в разложении можно не брать , так как потенциальная энергия равна 0 в положении равновесия. т.к. это константа. V= - ангармонизм.

Рассмотрим одномерную цепочку из атомов. X- равновесное расстояние.

- ряд Тейлора, β>0, положим , , . Для каждого воспользуемся каноническим распределением: вероятность того, что zпопадает z..z+dz, , 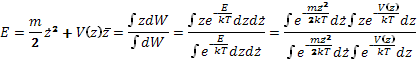преобразуем , , , , , -среднее отклонение от равновесия, 1 следствие нелинейности колебаний атомов в кристалле: линейное расширение (а-расстояние между атомами) α- коэффициент линейного расширения. . 2 конечная теплопроводность твердого тела: распространение тепла в твоердом веществе представляет собой диффузию фоновов. Ангармонизм приводит к тому, что фононы взаимодействуют друг с другом, длина свободного пробега резко уменьшается, как следствие уменьшеается коэфициент теплопроводности.

8. Модель свободных электронов в проводнике. Уровень Ферми и температура Ферми. Вырождение.

В самом грубом приближении: электроны свободно движутся внутри потенциального ящика.

ε- энергия электрона «от дна».

n=1 неопределенность гейзенберга:, ()³ – объем, занимаемый одним электрнным состоянием в фазовом пространстве.

Найдем сколько существует электронных состояний с энергией меньшей данной.

Z(E) – число электронных состояний. , - объем в фазовом пространстве. . Если рассматривать систему при Т=0, то энергия последнего заполненного состояния называется энергией (уровень) Ферми. Е_F- уровень ферми.

N- число валентных электронов. – концентрация, - энергия Ферми. Оценка Определим температуру Ферми Т_Fиз следующих соображений (k-постоянная Больцмана). Характерная энергия электрона. Е>>kTотсюда следует что электронный газ вырожден. (вырожденный Ферми – газ)