
Расходимость и интенсивность
.docxИзмерение распределения интенсивности излучения
Регистрация распределения интенсивности излучения является необходимым этапом для определения всех пространственно-энергетических параметров пучка, в том его сечений, проекций и моментов различных порядков. Параметры пучка, определенные в дальней зоне характеризуют его расходимость.
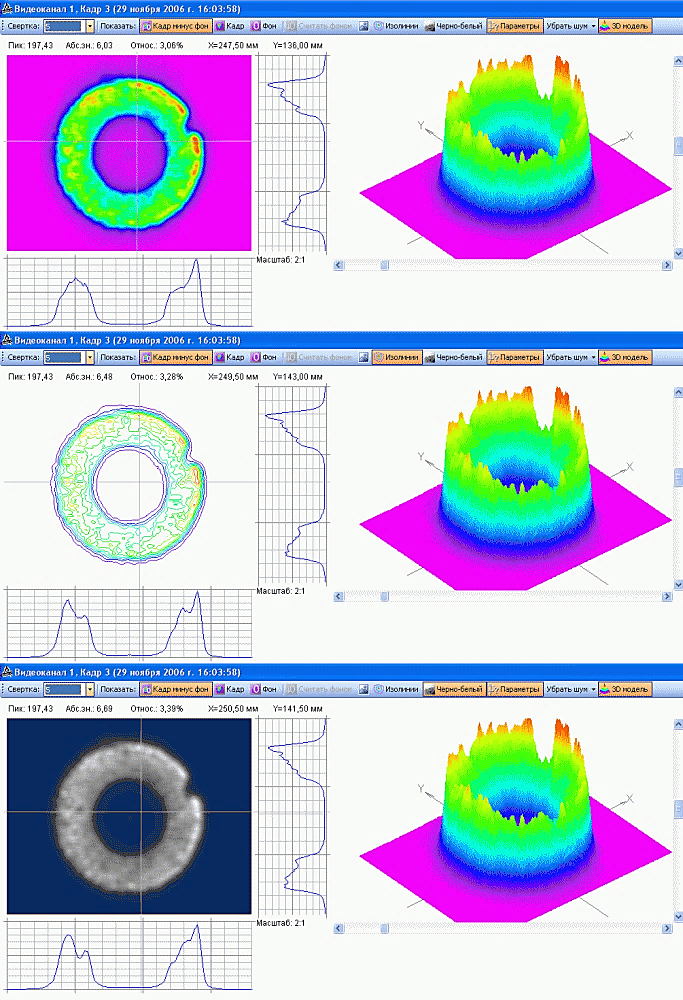
Три варианта отображения распределения интенсивности в ближней зоне:
с помощью цветовой зависимости; в виде изолиний; изменением яркости черно-белого изображения
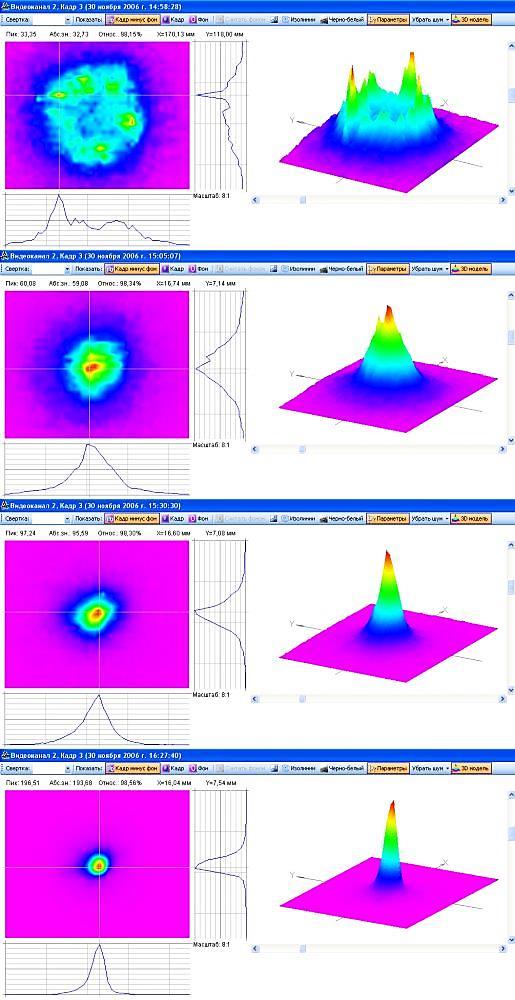
Регистрация интерфрограмм
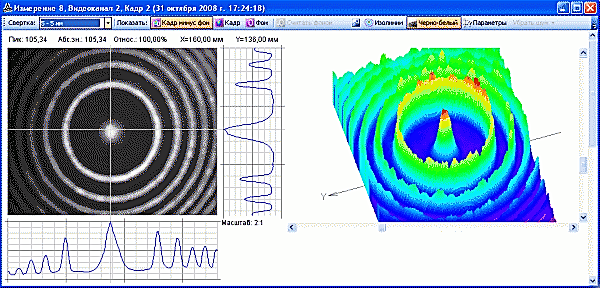
Гауссово распределение. Основные соотношения
Гауссово распределение известно всем. Но каждый раз, когда надо прикинуть соотношение параметров при оценке реального распределения, возникают трудности (надо либо искать книжку с таблицами, либо считать на компьютере).
Предельно упрощенный подход к проблеме (в случае одномерного распределения) изображен на рисунке.
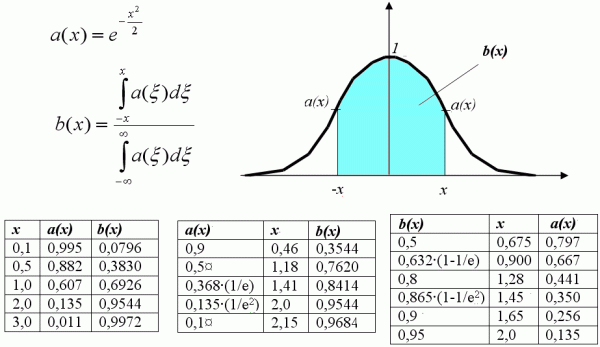
Здесь:
- х – отклонение от центра распределения, нормированное на «сигму» (на среднеквадратическое отклонение - СКО);
- а(х) – ордината Гауссова распределения, соответствующая х и нормированная на максимум распределения;
- b(х) – доля полной площади под кривой распределения а(х), заключенная в пределах от (–х) до (+х).
Поскольку из трех указанных величин в реальной жизни аргументом может быть любая, то приведены три таблицы, связывающие их.
Физический смысл приведенных соотношений поясним следующими примерами (в предположении, что ситуация дает достаточные основания полагать распределение Гауссовым). .
1. Ширина линии излучения определена по уровню 0,5 от максимума. Какая доля полной мощности распространяется в пределах этой ширины. Ответ: 0,76.
2. Результат измерений с вероятностью 0,95 должен находиться в некоторых пределах. Каковы эти пределы? Ответ: ±2 СКО.
3. По какому уровню интенсивности следует измерять ширину линейного пучка полупроводникового лазера, в пределах которой должно быть сосредоточено 0,9 полной мощности. Ответ: по уровню 0,256 от максимальной интенсивности.
Двумерное осесимметричное Гауссово распределение легко получается вращением функции а(х) вокруг центральной оси (х, при этом, становится радиусом). Для его описания удобно дополнительно использовать функциюс(х), соответствующую доле полного объема под поверхностью двумерного распределения в пределах круга радиусом х (см. рисунок).

Осесимметричное Гауссово распределение обладает уникальными свойствами. Например,
функция а(х) не только описывает изменение плотности в центральном сечении (а при нормировании на единицу и в любом другом сечении), но и распределение в любой проекции двумерного распределения.
Аналогично, функция b(х) , соответствует не только доле полной площади под кривой сечения, заключенной в пределах от –х до +х, но и доле полного объема под поверхностью в пределах полосы шириной 2х.
Очевидно, что при увеличении х функция b(х) нарастает быстрее, чем функция с(х).
Кроме того, нетрудно показать, что для любого х значение с(х) численно равно 1- а(х). Взаимосвязь всех параметров отражена в таблице.
Физический смысл приведенных соотношений поясним следующими примерами.
Допустим, мы располагаем сканирующим измерителем ширины пучка с использованием тонкой щели или края ножа. Пучок непрерывного излучения можно считать Гауссовым. Тогда:
1.Для измерения диаметра пучка, в пределах которого содержится 0,5 полной мощности необходимо определить ширину полосы, в пределах которой содержится 0,7620 полной мощности.
2. Для измерения диаметра пучка по уровню 0,135 (1/е2) интенсивности необходимо определить ширину полосы, в пределах которой содержится 0,9544 полной мощности.
Измерение расходимости лазерного излучения
Измерение расходимости пучка лазерного излучения основано на предварительной регистрациираспределения интенсивности излучения по сечению пучка в дальней зоне. Дальнейшая математическая обработка этого распределения позволяет определить его сечения, проекции, а также ряд моментов различных порядков. На этой основе и определяется угловая ширина пучка, т.е. его расходимость.
Советские стандарты и соответствующая практика предусматривали два определения расходимости пучка.
По интенсивности: плоский угол при вершине конуса вращения вокруг оптической оси, средняя сила излучения (энергии или мощности) на образующих которого составляет заданный уровень от максимальной силы излучения в данном пучке.
По энергии: плоский угол при вершине конуса вращения вокруг оптической оси, в пределах которого распространяется заданная доля излучения (энергии или мощности) от полного излучения пучка.
Оптической осью при этом считалась линия, проходящая через энергетический центр (центр тяжести) пучка в дальней зоне, т.е. на бесконечном удалении от лазера. Об эллиптичности пучков вопрос ставился, как правило, только как о временном недостатке, подлежащим устранению в ходе дальнейших работ.
В практическом применении того или иного из двух указанных критериев, а также того или иного «заданного уровня» наблюдался разнобой, обусловленный попытками ответить на два вопроса: - какой параметр и по какому уровню лучше отражает назначение лазера? - какой параметр и по какому уровню может быть проще и надежнее измерен? Только естественное желание, чтобы параметр был еще и наиболее репрезентативным для проведения сопоставительного анализа с другими лазерами, в том числе с зарубежными, несколько сужало выбор. В результате, как правило, использовались 4 варианта: - 2 уровня по интенсивности 0,5 или 1/е2 =0,135; - 2 уровня по энергии 0,5 или (1-1/е2)=0,865.
В настоящее время в плане подготовки к вступлению в ВТО, происходит присоединение России к международным стандартам, в том числе и в области измерения лазерных параметров. В отличие от советской «свободы выбора» стандарт ISO 11146 устанавливает одно-единственное определение расходимости как углового размера, определенного на основе вторых моментов (двух дисперсий и одного смешанного момента) распределения силы изучения (энергии или мощности) в пучке. В первых редакциях этого стандарта было, правда, примечание, что он не распространяется на лазеры с неустойчивыми резонаторами и, вообще, на пучки с резко ограничивающей апертурой. Однако в последних редакциях это примечание исчезло, что наводит на размышления.
Разумеется, для Гауссовых пучков данное определение никаких возражений не вызывает, тем более что для них данный угол равен углу по интенсивности на уровне 1/е2 =0,135 и углу по энергии на уровне (1-1/е2)=0,865. Однако в случаях, когда распределение в пучке сильно отличается от Гауссова, слепое следование указанному стандарту может оказаться нецелесообразным (см. примеры ниже).
Для понимания сути проблемы при измерении расходимости рассмотрим 8 вариантов волнового фронта на выходной апертуре лазера и 8 соответствующих распределений излучения в дальней зоне, формирующихся в результате свертки отдельных составляющих расходимости. Они разбиты на 2 группы: 1)пучки с резко ограничивающей апертурой и 2)Гауссовы пучки. У пучков первой группы интенсивность выходящего излучения на краю пучка резко падает до нуля, благодаря чему наблюдается относительно сильная дифракция. У Гауссовых пучков, конечно, тоже есть ограничивающая апертура, но ее край проходит там, где интенсивность выходящего излучения пренебрежимо мала, а диаметр отсчитывается там, где интенсивность излучения составляет 0,135 от максимального значения. Все варианты схематически отображены на рисунке.
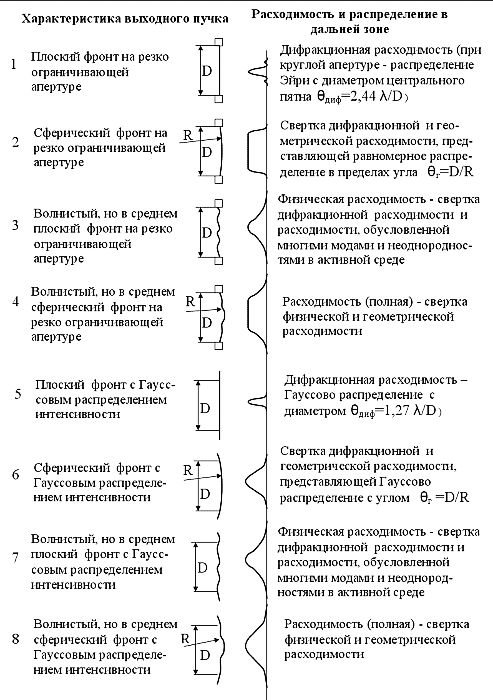
1. Расходимость пучка идеального излучателя с плоским фронтом определяется только дифракцией на выходной апертуре. Расчет может быть проведен для выходной апертуры любой конфигурации. Для круглой апертуры с диаметром D эта (дифракционная ) расходимость обычно оценивается угловым размером диаметра первого темного кольца на картине Эйри, в пределах которого распространяется 0,84 полной энергии или мощности). Эта составляющая присутствует всегда. 2.При сферическом волновом фронте с радиусом R (неважно сходящемся или расходящемся) на выходной апертуре, основную роль играет геометрическая составляющая расходимости, определяемая соотношением D/R . Эта составляющая, в принципе, сравнительно легко устраняется установкой в пучке в нужном месте подходящей линзы. 3.Если волновой фронт, оставаясь в среднем плоским, в более мелком масштабе имеет неровности, обусловленные как наличием многих мод так и неоднородностями активной среды, расходимость пучка значительно превышает дифракционную и называется физической. Эта составляющая расходимости является самой важной как для разработчиков, так и для потребителей. Она определяет так называемую фокусируемость пучка. В отличие от геометрической она уменьшается непросто и за ее уменьшение идет тяжелая и изнурительная борьба. 4.Наиболее общий случай пучка с резко ограничивающей апертурой, когда присутствуют все составляющие расходимости. 5.Гауссов пучок диаметром D с плоским фронтом, распространяясь в пространстве, всегда сохраняет Гауссову форму (если не учитывать влияние атмосферы). Дифракционная расходимость такого пучка несколько превышает отношение длины волны к диаметру пучка. В пределах этого угла (почти в два раза меньшего, чем у излучателя с резкой апертурой) распространяется 0,865 полного излучения (энергии или мощности). 6. Сферический фронт также не оказывает влияния на форму распределения. Пучок везде остается Гауссовым, но его угловое уширение из-за геометрической составляющей расходимости определяется соотношением D/R . 7. Физическая расходимость обусловленная как наличием многих мод так и неоднородностями активной среды, разумеется, имеет в общем случае не Гауссову форму, и, как указывалось ранее определяет фокусируемость пучка. 8. Полная расходимость включает все составляющие. Ее форма будет значительно отличаться от Гауссовой только при большой физической расходимости.
С точки зрения проведения практических измерений наиболее эффективным методом измерения расходимости является метод фокального пятна. При этом используется то обстоятельство, что линейные размеры в фокусе безаберрационной линзы строго пропорциональны угловым размерам в дальней зоне. В частности это относится к диаметру d и углу расходимости . Коэффициентом пропорциональности является фокусное расстояние линзы F . Таким образом, угол расходимости равен d/ F. Практические аспекты применения метода фокального пятна обсудим с использованием рисунка (все углы для наглядности утрированы).
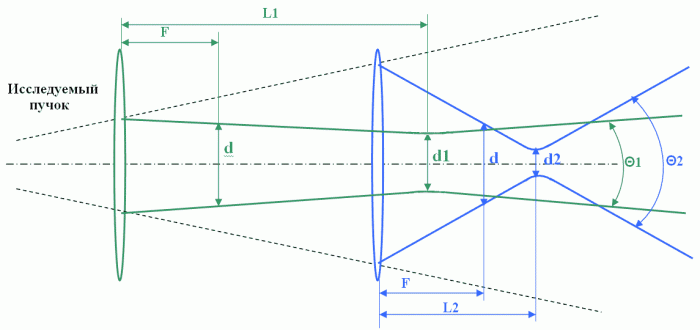
Бросается в глаза, что в зависимости от положения линзы в расходящемся пучке фокусировка пучка осуществляется по-разному. При близком расположении линзы к излучающей апертуре лазера (зеленый вариант) перетяжка пучка расположена далеко за фокусом линзы и имеет большой поперечный размер. При более дальнем расположении линзы перетяжка сильно уменьшается в размере и приближается к фокусу линзы.
Возникает вопрос: есть ли какие – либо инварианты, не зависящие от положения линзы? Есть; и их - два: 1) распределение интенсивности в фокусе линзы не зависит от ее положения; соответственно идентичными сохраняются значения диаметра d пятна и расходимости d/ F по любому критерию и по любому уровню; 2) произведение диаметра перетяжки на угол расходимости сфокусированного пучка , являющееся параметром качества пучка ВРР (Beam Parameter Product).
Если первый инвариант (полная расходимость) определяется непосредственно в ходе одного эксперимента, то для определения второго требуется дополнительная работа. В частности необходимо уточнить положение перетяжки и значение ее диаметра, а также определить угол расходимости сфокусированного пучка. Кроме того, если расходимость по п.1) может определяться по любому критерию, то для диаметра перетяжки, и для угла расходимости, используемых при определении параметра ВРР согласно п.2), в общем случае в качестве критерия пригоден только второй момент.
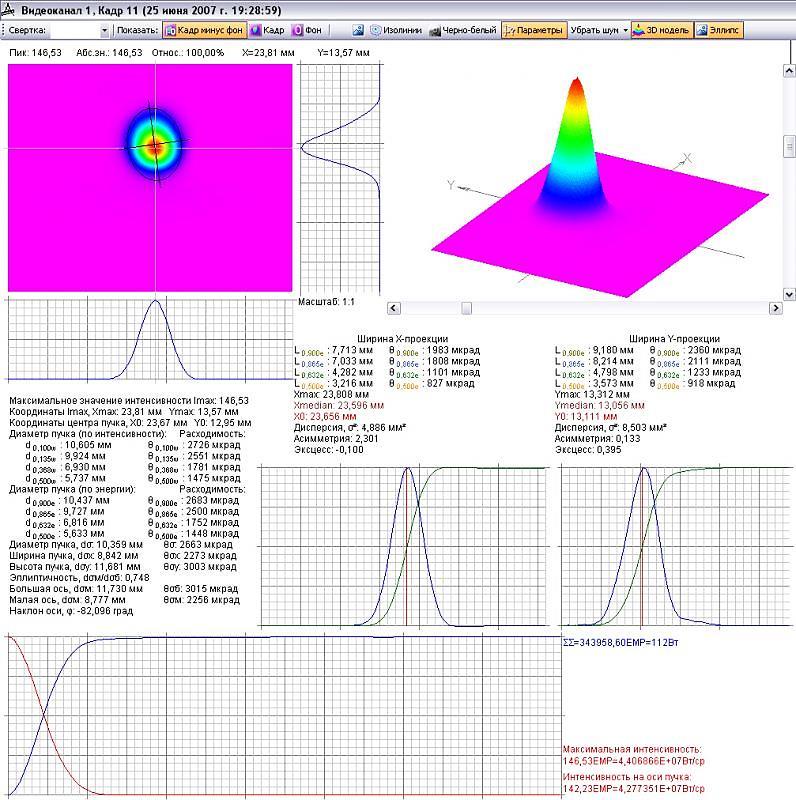
Качество лазерного пучка. Пример измерения.
В советской практике качество лазерного пучка стандартами не регламентировалось и, как правило, оценивалось «в дифракциях». Например, выражение «в пучке три дифракции» означало, что расходимость пучка в три раза больше дифракционной. При этом подразумевалось, что расходимость исследуемого пучка уже «очищена» от геометрической составляющей, поскольку в противном случае «количество дифракций» могло быть чрезмерно большим и давать явно заниженную оценку качества пучка. Оценка дифракционной расходимости производилась с использованием модели идеального излучателя с соответствующей выходной апертурой. В частности, для излучателя с круглой апертурой со значением диаметра пучка на выходной апертуре лазера D и длиной волны λ дифракционная расходимость определялась по формуле:
![]()
В пределах этого угла (первого темного кольца на картине Эйри) содержится 84% полной энергии излучения.
Что касается расходимости, то она измерялась по уровню интенсивности 0,135 (1/е2) от максимальной, исходя из тех соображений, что в пределах этого угла (по крайней мере для Гауссова пучка ) содержится практически такая же доля (86,5%) энергии.
Современные международные стандарты явно тяготеют к рекомендациям для исследований преимущественно Гауссовых пучков и группируются, в основном, вокруг двух оценок качества: ВРР иМ2 .
ВРР ( beam parameter product - произведение параметров пучка), определяется как произведение диаметра пучка в перетяжке на полный угол раходимости излучения (мм мрад). (Примечание: В некоторых источниках параметр ВРР определяют как произведение радиуса пучка в перетяжке на половину угла расходимости, т.е. величину в четыре раза меньшую. Поэтому, с целью исключения ошибки, лучше уточнить, что имеется в виду).
На практике измерение ВВР проводят с помощью фокусировки пучка безаберрацонной линзой.
Чем ВРР меньше, тем лучше качество пучка, т.е. тем под меньшим углом (на большем расстоянии) его можно собрать в меньшее по размеру пятно.
Оба сомножителя должны измеряться по второму моменту. ВРР явно зависит от длины волны и в дифракционном пределе равен 4λ/π .(два луча предельно высокого -дифракционного качества с длинами волн 10,6 мкм и 1,064 мкм по параметру ВРР отличаются на порядок -13,5 мм мрад для первого и 1,355 мм мрад для второго).
Параметр М2 , также называемый параметром распространения пучка , в соответствии со стандартомГОСТ Р ИСО 11146-1-2008 является наиболее используемым при проведении сопоставительного анализа различных лазеров. Его значение определяется путем деления параметраВРР на дифракционный предел 4λ/π. Таким образом, снимается зависимость параметра качества пучка от длины волны и он становится безразмерной величиной, показывающей во сколько раз он больше параметра дифракционно-ограниченного пучка с этой же длиной волны. Таким образом, М2 позволяет выразить расходимость пучка с диаметром перетяжки d следующим образом:
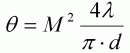
При дифракционной расходимости М2 , естественно, равен 1,0.
