Лекции Шкурбы В.В / Лекции Шкурбы В.В / 2 / LECTURE3

Лекция 3:

Практическое использование

табличного процессора.

3.1. Методы нахождения нулей функции.

Метод дихотомии.

Дихотомия - половинное деление.

…

Метод Ньютона. Касательная.

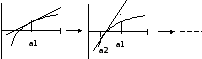
- уравнение касательной в т.х1

Далее находим точку пересечения касательной с осью ОХ

Процесс продолжается до тех пор, пока не будет достигнуто искомое значение.

Метод Ньютона эффективнее дихотомии и является итеративным.

Итеративный метод - метод вычисления следующего значения по предыдущему.

В табличных процессорах циклические вычисления производятся с помощью макрокоманд.

	A	............	AA	AB	AC
1	2			{Let \k,1}	Задание начальных значений k
2	4		\c	{Calc}	Метка и подсчет
3	7			{Let \k,\k+1}	Присвоение нового значения k
4				{If \k>N}{Quit}	Сравнение k и N
.......				{Branch \c}	Переход на метку
300

3.2. Леонтьевская модель межотраслевых связей

в табличном процессоре.

	1	2	3
400	50	150	100	100
500	100	200	150	50
600	150	150	150	150

, ãäå - валовый продукт i-ой отрасли

- продукт i-ой отрасли, потребленной j-ой отраслью.

- конечный продукт i-ой отрасли.

- технологический коэффициент (количество продукции i-й отрасли, затрачиваемой на единицу продукции j-й отрасли, определяемое технологией производства).

Леонтьевская формула межотраслевых связей:

;

Таким образом получена система линейных уравнений, позволяющая для каждого конечного продукта (вектор-столбец ) получить значения объема продукции каждой отрасли. Для этого можно использовать метод Зейделя (также итеративный).

В данном случае

Для таких систем последовательность сходится , независимо от порядка вычислений.

Сравнительная характеристика методов решения систем линейных алгебраических уравнений с n неизвестными:

• метод Крамера - 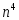вычислений

• ìетод Гаусса - вычислений

• метод Зейделя - 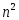вычислений

		.......		.....