2.4 Статистика рынка.

Оценка параметров входящих в основную модель, т.е. ,,, представляет собой статистическую проблему. Поскольку эффективность рынкапринята за ведущий факторF , то можно использовать уже описанную процедуру оценки с помощью МНК, применяемого к наблюдавшимся в прошлом последовательностям эффективностей ,каждой ценной бумаги и рынка в целом.

По аналогии с формулами (25) и учитывая определение (36), запишем выражение для оценок 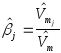;(37) где,- средние значения наблюдавшихся эффективностей ,,-оценка вариации эффективности рынка, -оценка ковариаций эффективности рынка и каждой ценной бумаги.

(38). Здесь T, как и ранее, - число обрабатываемых наблюдений. Для вычисления используется формула(39), где- средний квадрат отклонений от приближающей прямой: (40), интерпретируемый как оценка‘собственных’ вариаций.

Все приведенные оценки основываются только на истории рынка. Для ценных бумаг США расчеты проводятся регулярно. В качестве характеристики рынка в целом, как правило, используется уже упомянутый SP 500 Index. Аналитический отдел известной фирмы Merrill Lynch and Co., Inc. Ежемесячно составляет отчет ‘Market Sensivity Report’, содержащий таблицы, где для каждой из 500 фирм указаны вычисленные оценки величин бета, альфа, R-squared, ‘собственных’ вариаций (точнее, , называемых остаточными стандартными отклонениями в процентах). Указываются также характеристики точности оценок бета и альфа. В качестве истории ценных бумаг используются данные за последние 5 лет.

Приведем для иллюстрации одну строку из таблицы за ноябрь 1979г.

Sec. name	10/79 Close Price	Beta	Alpha	R-sqr.
TIME Inc.	43.250	1.24	1.39	0.36

Resid. Std Dev.	Std. of Beta	Error of Alpha	Adjusted Beta	Numb. of Observ.
6.84	0.21	0.9	1.16	60

B предпоследнем столбце указана величина, именуемая ‘приспособленная бета’, , вычисленная по формуле(41).

Такое приспособление позволяет улучшить прогнозирующие свойства исторической оценки бета () и основывается на гипотезе, что поведение акций, длительно котируемых на рынке, имеет тенденцию постепенно приближаться к поведению рынка в целом, т.е.приближается к 1. Вместе с тем это положение достаточно дискуссионно.

Более эффективным является введение поправок к ‘историческим’ бета на основе анализа влияния других факторов.

Статистические исследования рынка США показали, например, что эффективной является формула (42) гдеk₀- число, зависящее от того, к какому сектору экономики принадлежит данная корпорация (например 0,45 для базовых отраслей и 0,25 - для транспорта), k₁ равно 0,58, а коэффициент k₂ ,отражающий влияние размера S_j компании на оценку бета, отрицателен и равен -0,1. При этом размер S_j вычисляется как десятичный логарифм суммарной стоимости акций, выраженной в млн. долл. (например для компании с капиталом 100 млн. долл. принимается S_j=2).Формула (43) свидетельствует о том, что зависимость акций от поведения рынка различна в различных отраслях (например снижение общей эффективности рынка влияет на курс акций транспортных компаний слабее, чем на курс акций компаний, работающих в базовых отраслях) и что курс акции более крупных компаний менее чувствителен к колебаниям эффективности рынка. Подчеркнем, что формулы типа (41),(42) - лишь частные случаи более общего подхода, в котором исторические данные корректируются с помощью дополнительной информации о перспективах работы корпораций-эмитентов.