2.2 Метод ведущих факторов.

Как уже подчеркивалось, в экономической жизни все взаимосвязано, но есть факторы которые влияют сразу на все показатели. Например, уровень цен на ближневосточную нефть влияет на котировку акций почти всех компаний США, поскольку эта нефть покрывает более половины энергетических потребностей США. Если цена на нефть поднимается, то станет дороже бензин для автомобилей, уменьшиться спрос на бензин, на сами автомобили, на металл для их изготовления, повысятся цены на сельскохозяйственные продукты, поскольку затраты на топливо- основной компонент из себестоимости.

Рассмотрим один из таких ведущих факторов, не определяя пока его природу. Обозначим его F и будем считать, что эффективности всех вложений зависят от него. Простейшая форма зависимости- линейная, так что примем гипотезу (24). Как проверить такую гипотезу и оценить значение величин?

Простейшая процедура- метод наименьших квадратов (МНК).

Нанесем на диаграмму (рис.1) точки, каждая из которых имеет координаты , т.е. значения эффективностиj-ой ценной бумаги и ведущего фактора за период t. Попытаемся далее провести прямую так, чтобы сумма квадратов отклонения от нее всех точек была минимальной. Тангенс угла наклона этой прямой даст оценку коэффициентов, а отрезок, отсекаемый ею на оси, даст оценкуожидаемого значенияj случайного коэффициента .

Рис.1

Формальная процедура построения такой прямой приводит к следующим простым формулам :

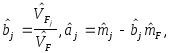где (25); (26),

т.е. - статистические оценки ожидаемых значений эффективностейи фактораF ,- оценки ковариаций эффективности и фактора, а- оценка вариации самого фактора.

Если гипотеза верна, то все отклонения от прямой вверх и вниз действительно являются случайными, и если в будущем возникнет новая ситуация, новая пара величин , то соответствующая точка расположится где-то в окрестности прямой.

Средний квадрат отклонений от прямой, найденный по истории ценной бумаги, дает оценку вариации a_j, которую назовем Ve_j. Такие расчеты можно провести по всем интересующим видам ценных бумаг.

Если ведущий фактор выбран удачно, то его влиянием определяются все случайные колебания эффективности, а собственные случайные отклонения e_j от детерминированной линейной связи оказываются взаимно некоррелированными. Таким образом, приходим к уточненной гипотезе (27), гдеe_j удовлетворяют условию отсутствия корреляции если (28), причем уже было введено обозначение для вариации ‘собственных’ случайностей (29)

Таким образом, при рассмотрении n ценных бумаг подлежат оценке n величин ,n величин ,n собственных вариаций , а также ожидаемое значение и вариация самого фактораи, итого 3n+2 параметров.

Оценить такое количество по (n+1)T значениям, содержащимся в историях (за T периодов) ведущего фактора и всех ценных бумаг, значительно проще и надежнее, чем напрямую оценивать величин ,, как это делалось ранее. Вместе с тем не трудно убедиться, что все величины ,можно вычислить, зная указанные параметры: (30) (31)

Следует, конечно, помнить, что все это упрощение опирается на принятую гипотезу.