2. Статистика финансового рынка.

2.1 Прямой статистический подход.

В развитых странах регулярно публикуются сведения о биржевом курсе ценных бумаг, прежде всего акций ведущих компаний. Таким образом, можно проанализировать последовательности, отражающие историю курсов и выплачиваемых дивидендов за достаточно длительный период. Имея эти данные, можно построить последовательности реальных эффективностей ценных бумаг за каждый квартал согласно определению:

Если R_j- эффективность ценных бумаг j-го вида за период t, то она равна (20), где - цена в начале периодаt, - дивиденды за периодt. В действительности теоретическая формула (1) должна быть уточнена. Следует учесть, что цена покупки (bid price) и цена продажи (ask price) различны, даже если эти операции относятся к одному и тому же периоду времени. Именно эта разность (bid-ask spread) составляет основной источник заработка профессионального торговца акциями (дилера). Эффективность вклада должна оцениваться по общему итогу операции, состоящей из покупки у дилера ценных бумаг по цене (ask price начала периода), получения дивиденда за период и продажа в конце периода (начале следующего) по цене 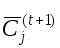(bid-price), которая ниже ask price того же момента на установленный для данного вида ценных бумаг процент (в среднем ~1%, но для акций крупных компаний процент ниже, а для мелких выше, что отражает трудоемкость сбыта менее солидных ценных бумаг). Таким образом, уточненная формула имеет вид: (21).

Предположим, что ряды таких данных подготовлены соответствующей информационной службой. Как связать их с принятой ранее теоретической моделью, в которой эффективности трактовались как случайные величины?

Логически простейший путь заключается в следующем: предположим, что наблюдаемые последовательности {, t=1,...,T; j=1,...,n} являются реализациями, выборками из совокупности случайных величин {},и , более того, значения эффективностей в будущем () также являются реализацией той же совокупности.

Эта гипотеза открывает принципиальную возможность статистической оценки параметров, характеризующих величины .

В соответствии с правилами статистики можно ввести оценки математических ожиданий как средних по выборкам: (22),(23).

Напомним некоторые особенности оценок. Не вдаваясь в тонкости математической статистики, подчеркнем лишь, что точность оценок тем выше, чем больше имеется исходных данных, и тем ниже, чем больше оцениваемых величин.

Реальные цифры таковы. Число ведущих компаний, акции которых котируются на биржах США и составляют основную (по общей стоимости) часть рынка, обычно оценивается в n=500 (такое число учитывается в наиболее популярном издании ‘Standard and Poor’s Index’). Длительность ежеквартальных временных рядов, имеющих смысл для статистической обработки, T=100 (экономические условия и даже сам список ведущих компаний за период более 25 лет слишком сильно изменяются, чтобы столь устаревшие данные считать представляющими ту же генеральную совокупность).

Таким образом, общий объем информации составляет 5*10⁴ чисел. Оценке же подлежат n величин и различных величин. Приn=500 получаем, что требуется оценить более 10⁵ величин , т.е. больше, чем исходных данных. Поэтому оценки ковариаций окажутся заведомо неточными.

В силу этого обстоятельства прямой статистический подход используется только для вычисления оценок , а также для оценки ковариаций между ‘самыми главными’ акциями в небольшом количестве, например количестве 30, на базе которых выводиться знаменитый индекс Доу-Джонса. При этом число данных 3000, а число оцениваемых величин ~500, что не так уж плохо.

Однако финансовый аналитик обязан давать рекомендации не только по немногим ведущим, а по возможно большему числу компаний, выдвигающих свои ценные бумаги на рынок (например наиболее подробный в США Wilshire Index учитывает 5000 видов ценных бумаг).