МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Государственный Университет Управления

Кафедра Экономической кибернетики

Лабораторная работа №3

по дисциплине:

«Методы социально-экономического прогнозирования»

на тему:

«Прогнозирование состояния социально-экономического объекта на основе восстановления весов критериев оптимальности»

Выполнил: студент ИИСУ

специальности ММиИОЭ IV-1

Мирончук Евгений

Проверила: Писарева О.М.

Москва 1999

Постановка задачи.

На практике управления и прогнозирования деятельности крупных систем особое место занимает задача определения весов частных критериев в критерии оптимальности социально-экономического объекта. Рассмотрим эту проблему в предположении о линейном характере зависимостей в модели планирования производственно-хозяйственной деятельности объекта.

Итак, пусть на практике в неявной форме фирмой решается следующая задача среднесрочного планирования: (система 1)

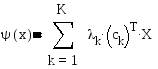
При этом фирма руководствуется в своих решениях некоторой системой предпочтений относительно целей своей деятельности. Формально эта система выражается структурой вектора .

Для восстановления весов _k можно воспользоваться условиями Куна-Таккера. Это необходимые и достаточные условия достижения максимума целевой функции системы 1в точке X₀ Для задачи эти условия имеют вид:

, где

I(X⁰) - множество активных ограничений

J(X⁰) - множество активных ограничений

- градиент функции точке X⁰

y_i - множитель Лагранжа или двойственная оценка соответствующего ограничения.

v_j - неотрицательное число, связанное с соответствующими активными ограничениями подсистемы.

Таким образом X⁰ является оптимальным планом системы 1 в том и только в том случае, если удастся подобрать произвольные числа y_i, и неотрицательные v_j, такие, что выполняется указанное выше векторное равенство. Преобразуя его, получаем следующую систему уравнений (2):

Общее решение системы (2) дает множество возможных весов lk и если оно состоит более чем из одного элемента, то все допустимые наборы весов  входящие в него, могут использоваться для прогнозирования поведения социально-экономического объекта. Если же множество  пусто, это значит, что использованы не все частные критерии или сама схема неправильно описывает систему предпочтений лица принимающего решения от имени объекта.

Этап 1.

На основе исходной информации об условиях функционирования объекта в течение одного периода времени осуществляем математическую формализацию задачи восстановления критерия оптимальности.

Исходные данные. 3-й период.

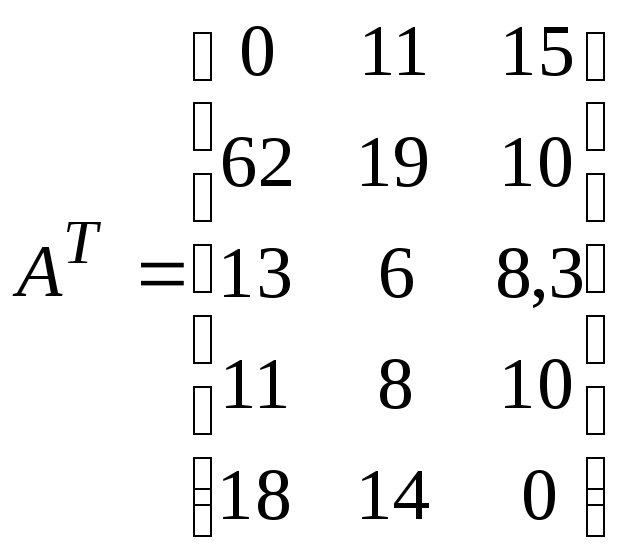
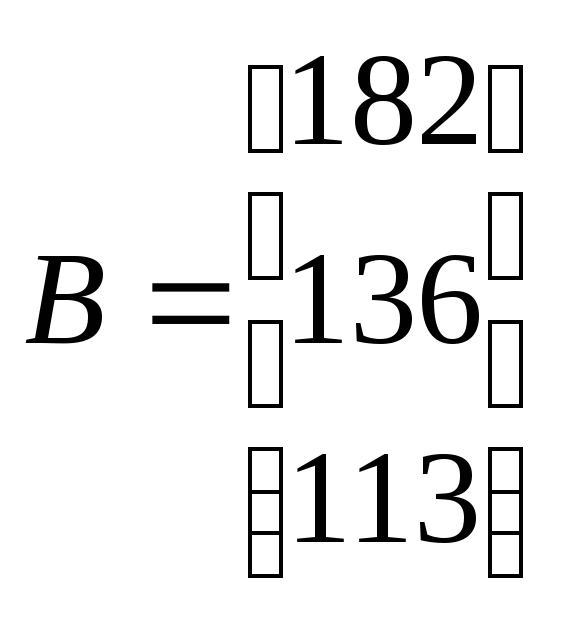
Рассматриваются 2 частных линейных критерия оптимальности, которым соответствуют вектора коэффициентов:

В этих условиях был выбран план:

Множество активных ограничений : I={1,2}

Множество активных ограничений : J={1,2,3}

Запишем систему (2):

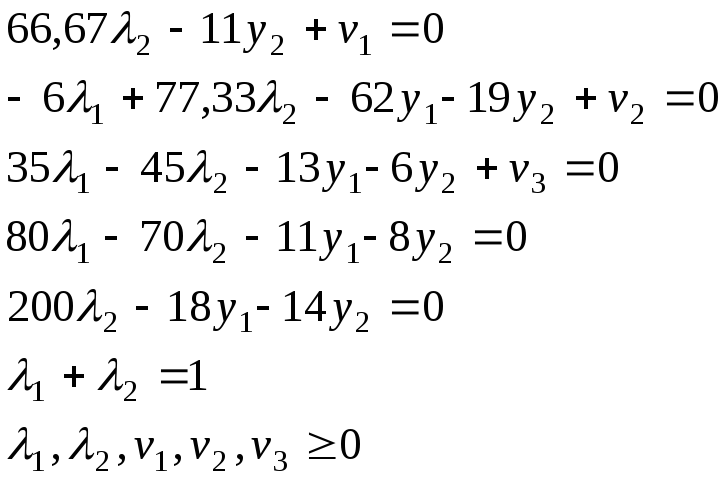
Для того, чтобы найти решение этой системы с помощью пакета BLP преобразуем эту систему следующим образом: введем фиктивные переменные и минимизируем их сумму в целевой функции.

Т.к. у может принимать любой знак, а ВLP предполагает, что на все переменные накладывается ограничение неотрицательности, то будем задавать у с помощью следующего выражения:

.

Решим эту систему с помощью пакета решения задач линейного программирования BLP. Результаты в Приложении №1.

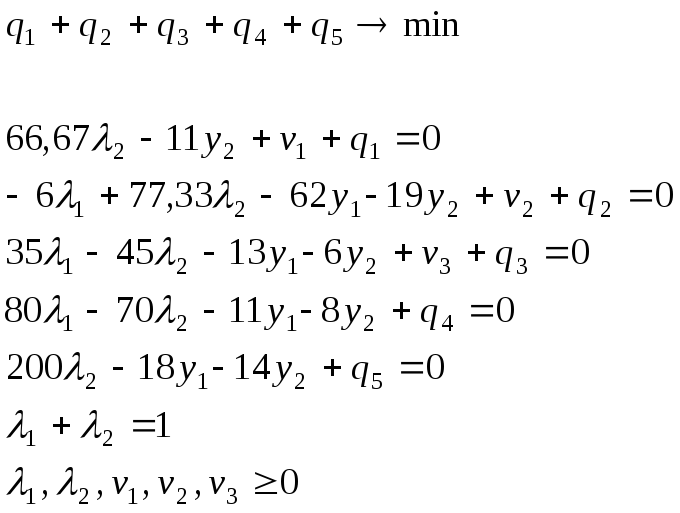
Вектор  имеет вид :

Анализ.

1 Система имеет множество решений (т.к. не все оценочные коэффициенты при небазисных переменных строго положительные). Для нахождения крайних точек решаем две системы, минимизируя соответственно ₁ и ₂.Получаем следующие решения:

Результаты в см. Приложениях №№2,3.

Поэтому общее решение системы задается формулой:

,

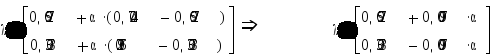где  принадлежит отрезку [0;1].

Этап 2.

Восстановим критерий оптимальности фирмы если существует ряд наблюдений за несколько периодов времени. Для этого решим систему (2) совместно для каждого периода:

Исходные данные. 1-й период.

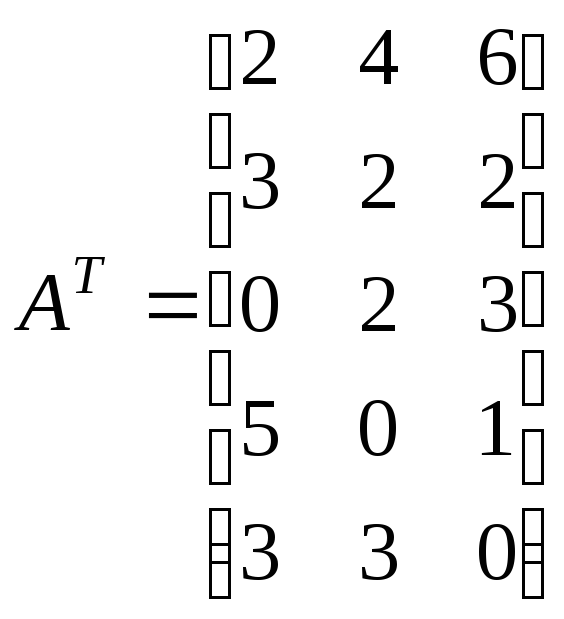
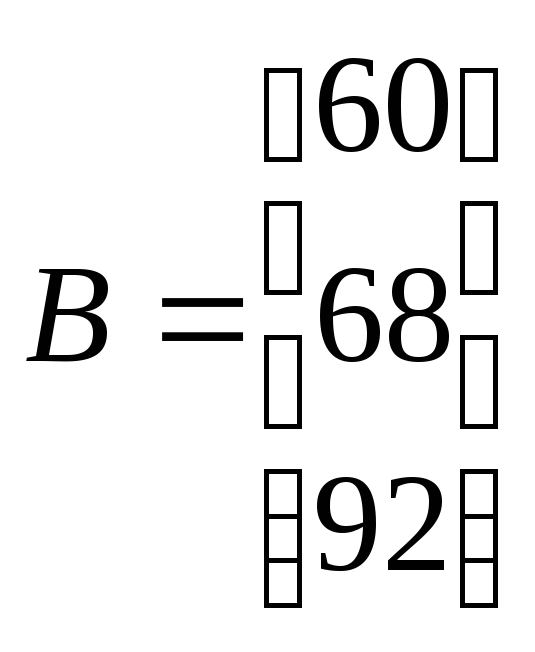
Рассматриваются 2 частных линейных критерия оптимальности, которым соответствуют вектора коэффициентов:

В этих условиях был выбран план:

Множество активных ограничений : I={2,3}

Множество активных ограничений : J={3,4,5}

Запишем систему (2):

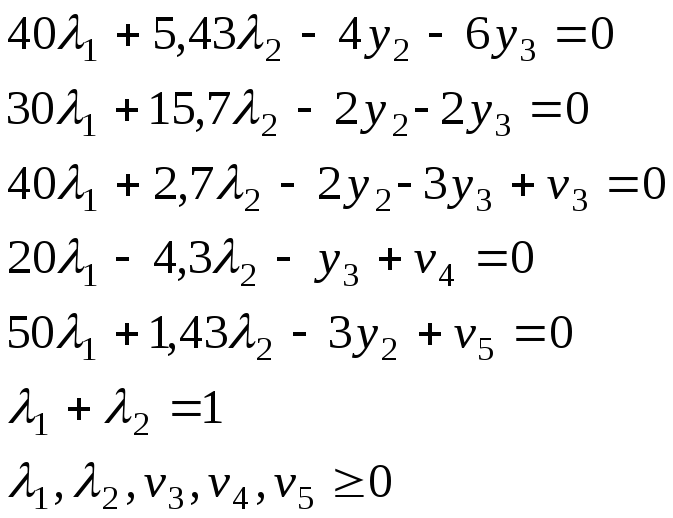
Исходные данные. 2-й период.

Рассматриваются 2 частных линейных критерия оптимальности, которым соответствуют вектора коэффициентов:

В этих условиях был выбран план:

Множество активных ограничений : I={1,2,3}

Множество активных ограничений : J={4,5}

Запишем систему (2):

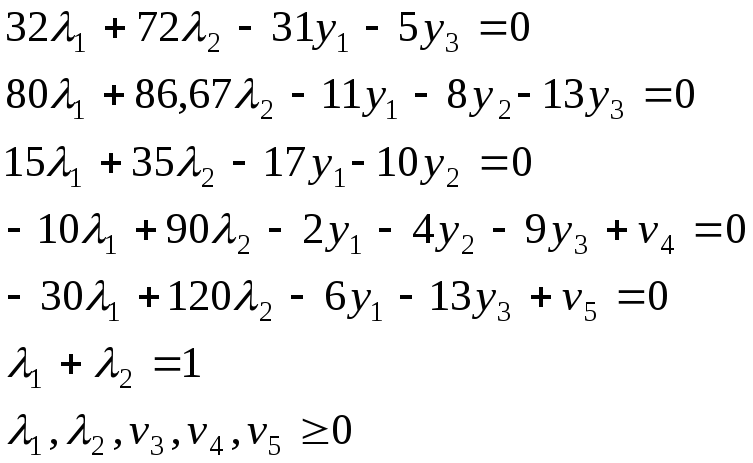
Система для 3-его периода была составлена выше.

Для составления совместной системы воспользуемся следующей предпосылкой: будем минимизировать расстояние от оптимального решения всей системы до оптимальных решений каждой подсистемы в отдельности. Это расстояние можно измерять как сумму модулей отклонений по весам: .

Тогда вектор -как оптимальное решение всей системы - определяется из решения следующей задачи:

Тогда искомая система примет следующий вид:

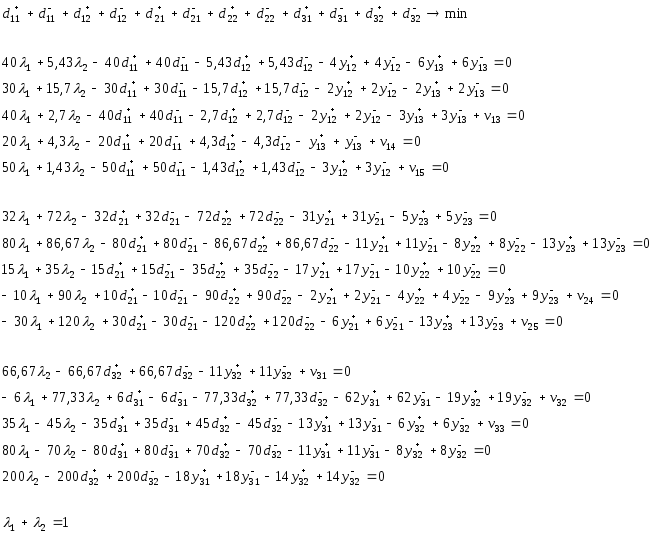
Решая данную систему в пакете BLP получаем единственной оптимальное решение (см. Приложение №4).