
Министерство общего и профессионального образования российской федерации
Государственный Университет Управления
Кафедра Экономической кибернетики
Домашняя работа №1
по дисциплине:
«Методы социально-экономического прогнозирования»
на тему:
«Прогнозирование с использованием авторегрессионных моделей»
Выполнил: студент ИИСУ
специальности ММиИОЭ IV-1
Мирончук Евгений
Проверила: Писарева О.М.
Москва 1999
Исходные данные для выполнения домашней работы №1 представлены в Приложении №1
Как известно аддитивная (или мультипликативная) модель временного ряда состоит из детерминированной (dt) и случайной(t) составляющей:
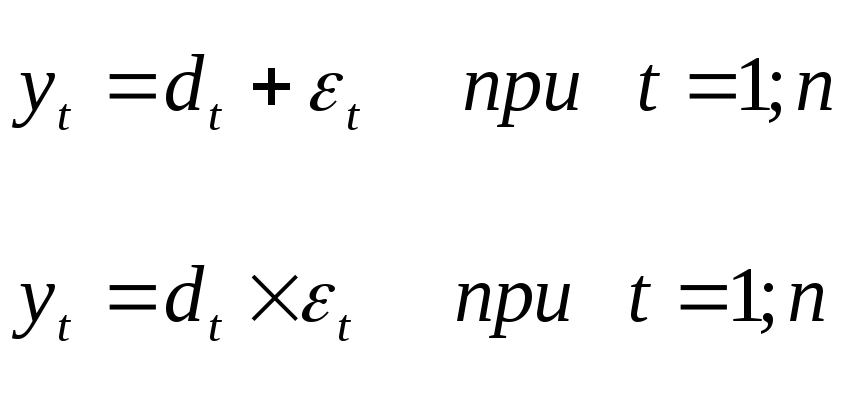
В свою очередь, детерминированная составляющая может включать в себя: тренд (trt), сезонную (st) и циклическую (ct) компоненты
![]()
Опыт показывает, что обычно временной ряд не удается полностью описать одной лишь детерминированной составляющей. Поэтому необходимо исследование поведения случайной составляющей, что и будет сделано в данной работе.
Итак, для изучения случайной составляющей необходимо избавится от детерминированной части временного ряда. Но прежде нужно определить какая из частей детерминированной составляющей присутствует в исходном временном ряде. Из графического представления временного ряда (Приложение №1) можно с большой уверенностью говорить об отсутствии сезонной и циклической составляющей. Определение же трендовой функции предполагает выполнение ряда действий:
проверка гипотезы о наличие тенденции в развитии;
в зависимости от выполнения пункта 1 построение самой трендовой модели.
Данный ряд действий по выявления трендовой составляющей был проделан в лабораторной работе №1. Трендовая функция, наилучшим образом описывающая исходный временной ряд, имела следующий вид:
![]() (полином
4 порядка)
(полином
4 порядка)
Оценки параметров данного тренда приведены в Приложении № 2.
![]()
Теперь можно приступать к непосредственному изучению случайной составляющей, выразив ее следующим образом:
![]()

Далее будем работать с рядом остатков t.
На основе полученного ряда остатков t(30 значений) необходимо определить существует ли их автокорреляция. Если существует, то нужно построить авторегрессионные модели этих остатков. На основе полученных моделей произвести прогноз на один период вперед (на 31 период). Чтобы построить более точный прогноз предполагается провести ряд опытов. Для этого рядtразбивается на два участка: тестовый (25 значений) и проверочный (5 последних значений исх. ряда). Используя, полученные на основе значений тестового участка, авторегрессионные модели, строим прогноз на 5 периодов вперед (дляy). Затем, сравнивая прогнозные значенияyсо значениями проверочного участка, выбираем наилучшую авторегрессионную модель, с помощью которой и будет построен прогноз на 31 период
I.
Авторегрессионые модели можно применять при прогнозировании изучаемых экономических показателей динамического ряда только при выполнении следующих предпосылок:
отклонения от тренда tявляются случайными, не зависящими от времени.
отклонения от тренда tпредставляют собой стационарный в широком смысле случайный процесс.
отклонения от расчетных значений, полученных по авторегрессионной модели, имеют нормальный закон распределения с математическим ожиданием, равным 0.
в ряду отклонений от расчетных значений, полученных по авторегрессионной модели, отсутствует автокорреляция.
Проверим относительно случайной компоненты tгипотезу о том, что она представляет собой стационарный процесс.
Для проверки случайного характера tприменимкритерий серий, основанный на медиане. Суть данного метода заключается в следующем:
Расположим члены анализируемого временного ряда tв порядке возрастания;
Определим выборочную медиану x(n) medпо формуле:

Образуем серии из плюсов и минусов:

Определяем общее число серий (последовательности плюсов и минусов) (t) и протяженность самой длинной серии(t)
Отклонения от тренда будут случайными, если выполнены следующие неравенства при 5 % уровне значимости:
![]()
![]()
Применим данный критерий к нашему ряду t. Расчеты представлены вПриложении №3.
![]()
![]()
![]()
Так как
![]() <
7,91 и
<
7,91 и![]() >
8,199 , то с полной уверенностью можно
сказать, что рядtносит случайный характер и не зависит
от времени.
>
8,199 , то с полной уверенностью можно
сказать, что рядtносит случайный характер и не зависит
от времени.
Для доказательства того, что ряд tпредставляет собой случайный процесс в широком смысле, находятся значения автокорреляционной функции для случайного компонента, используяn, (n-1), (n-2) ... (n-k) числа уровней ряда. В результате получаютrгрупп коэффициентов автокорреляции, в каждой из которых содержится (p+1) коэффициентов. Далее, используяz-критерий Фишера, устанавливается однородность коэффициентов автокорреляции, входящих в одну группу. Однородность коэффициентов автокорреляции дает возможность сделать вывод о том, что отклонения представляют собой стационарный в широком смысле случайный процесс.
Проверим выполнение данного условия для нашего ряда.
Общая формула для расчета коэффициента автокорреляции порядка выглядит следующим образом:
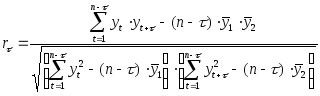
При расчете коэффициентов автокорреляции с ростом порядка число коррелируемых пар уменьшается, а при небольшом числе наблюдений значимыми оказываются высокие коэффициенты корреляции. Отсюда следует, что наибольшее значение должно быть таким, чтобы число пар наблюдений оказалось достаточным для вычисления коэффициентовr. В практике ориентируются на правило n/4. Таким образом, в нашем случае25/4=6,25=6.
|
Количество |
|
Сдвиги | |||||
|
наблюдений |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
25 |
r |
0,15368 |
-0,45087 |
-0,52950 |
0,05033 |
0,27455 |
0,15076 |
|
z |
0,15491 |
-0,48579 |
-0,58945 |
0,05037 |
0,28178 |
0,15191 | |
|
24 |
r |
0,18016 |
-0,46181 |
-0,53302 |
0,05607 |
0,27297 |
0,14908 |
|
z |
0,18215 |
-0,49960 |
-0,59435 |
0,05613 |
0,28007 |
0,15020 | |
|
23 |
r |
0,19396 |
-0,48765 |
-0,56313 |
0,06576 |
0,28786 |
0,16953 |
|
z |
0,19644 |
-0,53297 |
-0,63741 |
0,06586 |
0,29623 |
0,17118 | |
|
22 |
r |
0,19570 |
-0,48641 |
-0,56506 |
0,06542 |
0,28592 |
0,16482 |
|
z |
0,19825 |
-0,53134 |
-0,64023 |
0,06551 |
0,29412 |
0,16634 | |
|
21 |
r |
0,19414 |
-0,48603 |
-0,56562 |
0,06745 |
0,29074 |
0,16222 |
|
z |
0,19664 |
-0,53085 |
-0,64106 |
0,06755 |
0,29937 |
0,16367 | |
|
|
Z ср |
0,18568 |
-0,51611 |
-0,62050 |
0,06108 |
0,29031 |
0,16066 |
|
|
ХИ ^ 2 |
0,02301 |
0,03273 |
0,04668 |
0,00380 |
0,00526 |
0,00575 |
Расчетное значение
![]() (при=0,05;=5).
Видно, что фактическое значение
(при=0,05;=5).
Видно, что фактическое значение![]() меньше
меньше![]() .
.
Следовательно, можно утверждать, что гипотеза об однородности коэффициентов автокорреляции каждой группы принимается. Это означает, что случайный компонент представляет собой стационарный в широком смысле случайный процесс.
Анализируя значения автокорреляционной функции, можно предположить порядок авторегрессионной модели. Из таблицы видно, что начиная с 4 сдвига прослеживается уменьшение значений автокорреляционной функции, т.е. с 4 периода связь с прошлым ослабевает. Это говорит о том, что в данном случае нужно строить авторегрессионые модели не выше 3 порядка.
А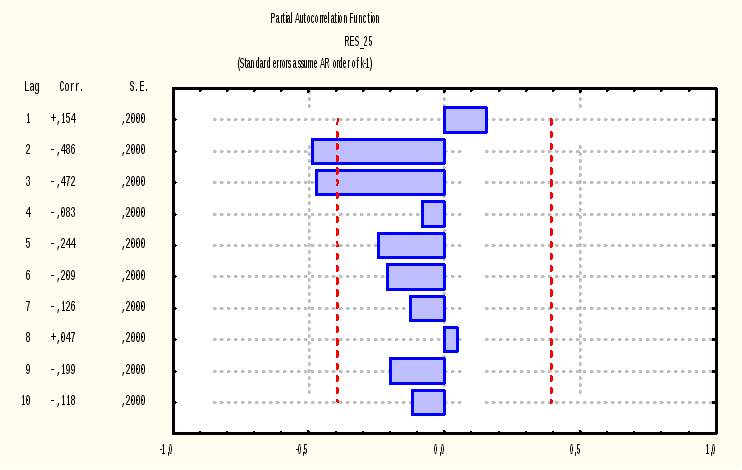 налогичный
вывод (о порядке регрессионной модели)
можно сделать из анализа графика
корелограммы:
налогичный
вывод (о порядке регрессионной модели)
можно сделать из анализа графика
корелограммы:
Из графика видно, что наибольшее значение частная автокорреляционная функция достигает при 2 и 3 сдвигах (2-й и 3-й столбцы выходят за пределы доверительной «трубы»). Следовательно, как уже было сказано выше, мы можем стоить авторегрессионные модели не выше 3 порядка.
Построим две авторегрессионные модели (см. Приложение № 4):
а) модель второго порядка: ![]()
б) модель третьего порядка: ![]()
Проведем дисперсионный анализ:
Для оценки модели в целом рассчитывается F-стат.
![]() ,
где
,
где![]() ,
,![]() .
ЗатемF-стат сравнивается
сF-табл при степенях
свободы
.
ЗатемF-стат сравнивается
сF-табл при степенях
свободы![]() .
ЕслиF-стат >
F-табл, то можно сделать вывод о
значимости модели в целом.
.
ЕслиF-стат >
F-табл, то можно сделать вывод о
значимости модели в целом.
Для оценки параметров модели рассчитывается t-стат.
![]() ,
где
,
где![]() ,
диагональные элементы есть дисперсии
свободного члена и коэффициентов
регрессии,Z- матрица
независимых переменных;
,
диагональные элементы есть дисперсии
свободного члена и коэффициентов
регрессии,Z- матрица
независимых переменных;![]() .
Затемt-стат сравнивается
сt-табл при степени
свободы
.
Затемt-стат сравнивается
сt-табл при степени
свободы![]() .
Еслиt-стат >
t-табл, то делаем вывод о значимости
параметра.
.
Еслиt-стат >
t-табл, то делаем вывод о значимости
параметра.
Для построения доверительного интервала параметров модели воспользуемся следующей формулой:
![]()
Коэффициент детерминации R^2 показывает на сколько точно данная модель описывает динамику изменения показателя во времени.
 .
.
Результаты дисперсионного анализа (см. Приложение №4) показали, что в обеих моделях коэффициент приt-1 незначим (по критерию Стьюдентаtрасчетное<tтабличноепри= 0,05). Следовательно, исключивt-1, нам необходимо построить модели следующего вида:
(1) ![]()
(2) ![]()
Оценка параметров этих моделей будет сделана в ППП STATGRAFICS в режиме REGRESSION ANALYSIS (см. Приложения № 5,6).В итоге получаем:
(1) ![]()
(2) ![]()
Дисперсионный анализ показал, что параметры данных моделей, а также модели в целом значимы.
Теперь посмотрим подчиняется ли ряд остатков zt(обеих моделей) закону нормального распределения.
Для этого необходимо будет рассчитать показатель асимметрии (А) и эксцесса (Э), и их среднеквадратические ошибки АЭ.
Уровни ряда являются нормально распределенными, если выполняются следующие условия (для выборочной совокупности):
![]()
![]() ,
,
где коэффициенты асимметрии и эксцесса определяются по формулам:
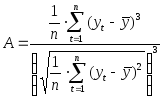
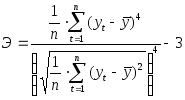
а среднеквадратические ошибки коэффициентов асимметрии и эксцесса - по формулам:
![]()
![]()
Если выполняется хотя бы одно из неравенств:
![]()
![]() ,
,
то данные не являются даже приблизительно нормальными и их применение в дальнейшем анализе не рекомендуется.
Рассчитаем, выше приведенные показатели, для zt, полученного в результате построения модели (1). Расчеты смотрите вПриложении № 7.
![]()
![]()
![]()
![]()
![]() выполняется
выполняется
![]() выполняется
выполняется
![]() не выполняется
не выполняется
![]() не выполняется
не выполняется
Вывод: отклоненияzt, полученные в результате построения модели (1), имеют нормальный закон распределения с математическим ожиданием0.
Теперь проведем подобный расчет для zt, полученного в результате построения модели (2). Расчеты смотрите вПриложении № 8.
![]()
![]()
![]()
![]()
![]() выполняется
выполняется
![]() выполняется
выполняется
![]() не выполняется
не выполняется
![]() не выполняется
не выполняется
Вывод: отклоненияzt, полученные в результате построения модели (2), имеют нормальный закон распределения с математическим ожиданием0.
Теперь необходимо доказать, что в ряду ztотсутствует автокорреляция.
Для доказательства используем критерий
Дарбина-Уотсона. Гипотеза о наличии
автокорреляции проверяется с помощью
случайной величины
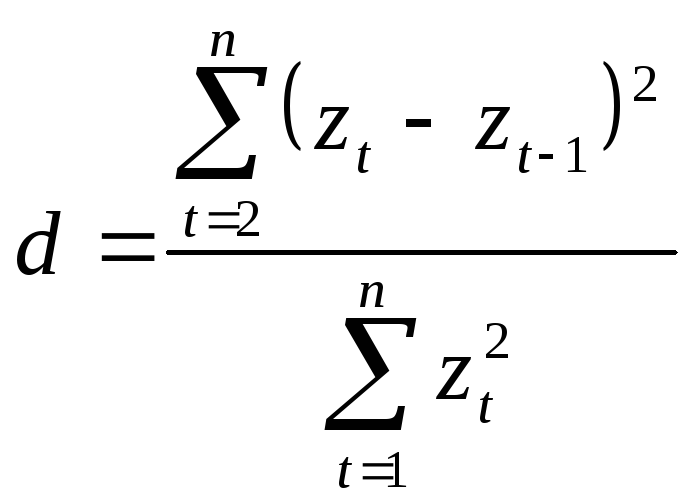 .
.
Возможные значения критерия находятся в интервале 0 - 4. Если авторегрессия в ряду отсутствует, то значение критерия dколеблются вокруг 2. Эмпирическое значениеdсравнивается с табличным значением. При сравнении расчетногоdс табличным может получиться один из трех вариантов:
 - ряд содержит автокорреляцию.
- ряд содержит автокорреляцию.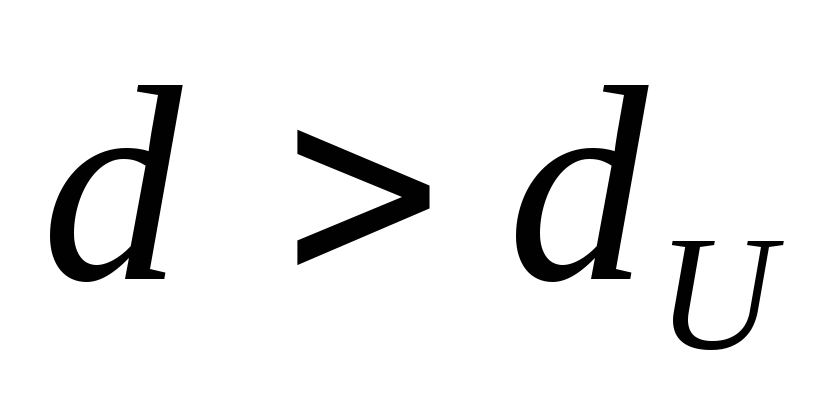 -
автокорреляция отсутствует.
-
автокорреляция отсутствует.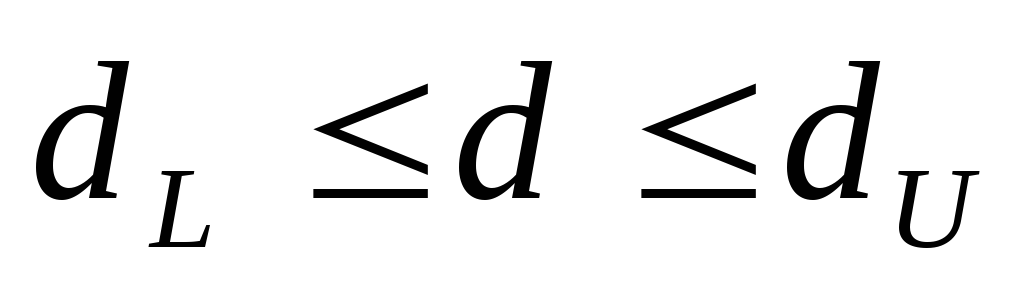 -
необходимо дальнейшее исследование
автокорреляции.
-
необходимо дальнейшее исследование
автокорреляции.
Величина критерия dразлична при положительной и отрицательной
автокорреляции; при отрицательной
автокорреляцииdнаходится
в интервале 2 - 4, тогда для проверки
следует определить величину![]() .
.
Проверим выполнение данного условия для zt, полученного в результате построения модели (1). Расчетное значение статистики Дарбина-Уотсона приведено вПриложении № 5.
![]()
![]()
![]() -
берутся из таблицы распределения
критерия Дарбина-Уотсона (n=25).
-
берутся из таблицы распределения
критерия Дарбина-Уотсона (n=25).
![]()
Вывод: так как![]() ,
то гипотеза об отсутствии автокорреляции
в рядуztпринимается.
,
то гипотеза об отсутствии автокорреляции
в рядуztпринимается.
Проверим выполнение условия для zt, полученного в результате построения модели (2). Расчетное значение статистики Дарбина-Уотсона приведено вПриложении № 6.
![]()
![]()
![]() -
берутся из таблицы распределения
критерия Дарбина-Уотсона (n=25).
-
берутся из таблицы распределения
критерия Дарбина-Уотсона (n=25).
![]()
Вывод: так как![]() ,
следовательно, гипотеза об отсутствии
автокорреляции в рядуztпринимается.
,
следовательно, гипотеза об отсутствии
автокорреляции в рядуztпринимается.
Общий вывод: исходя из проделанных выше расчетов и проверок можно сделать утверждение о возможности использования авторегрессионных моделей (1) и (2) для прогнозирования показателя.
II.
Итак, прогнозные значения y ищем в следующем виде:
![]()
Результаты расчета прогнозных значений t иyt для модели (1) представлены вПриложении №9
|
L |
T+L |
yT+L |
|
1 |
-0,4506 |
24,5960 |
|
2 |
-0,7818 |
24,6049 |
|
3 |
0,2038 |
28,8015 |
|
4 |
0,3535 |
35,6883 |
|
5 |
-0,0922 |
46,2094 |
КТ= 0,080
Результаты расчета прогнозных значений t иyt для модели (2) представлены вПриложении №9
|
L |
T+L |
yT+L |
|
1 |
0,35077 |
25,3974 |
|
2 |
-1,128 |
24,2587 |
|
3 |
-0,95321 |
27,6445 |
|
4 |
0,26113 |
35,5959 |
|
5 |
0,89657 |
47,1982 |
КТ= 0,089
По значению коэффициента Тейла можно сказать, что лучшие прогнозы для ytполучаются при использовании авторегрессионной модели (1). Поэтому, при построении прогноза на 31 период будет использована авторегресионная модель (1) случайной составляющей.
III.
Для удобства построения прогноза на 31 период сделаем следующее:
из уравнения трендовой модели выразим t ;
подставим это t в полученную авторегрессионную модель (1).
В результате преобразований получим модель прогноза:
![]()
Точечный
прогноз на 31 период:
![]()
Построим доверительный интервал прогноза. Для этого воспользуемся следующей формулой:
![]()
В результате получаем (см.Приложение №10):
![]()
![]()
![]()
IV. Оценка точности прогноза от длины периода упреждения при фиксированной длине ретроспективного периода.
|
Период упреждения (L) |
Кт | |
|
Используя при прогнозе модель (1) |
Используя при прогнозе модель (2) | |
|
5 |
0,08 |
0,089 |
|
4 |
0,074 |
0,075 |
|
3 |
0,046 |
0,044 |
|
2 |
0,059 |
0,042 |
Из таблицы видно, что при уменьшении периода упреждения значения Кт заметно уменьшаются.
Приложения
Приложение № 1
|
t |
Y |
Y=a+b*t+c*t^2+d*t^3+e*t^4 |
(t) |
|
1 |
30,0 |
33,4574 |
-3,4574 |
|
2 |
37,4 |
32,0842 |
5,3158 |
|
3 |
31,9 |
33,0748 |
-1,1748 |
|
4 |
36,7 |
35,8636 |
0,8364 |
|
5 |
41,0 |
39,9339 |
1,0661 |
|
6 |
43,7 |
44,8178 |
-1,1178 |
|
7 |
49,7 |
50,0961 |
-0,3961 |
|
8 |
53,9 |
55,3986 |
-1,4986 |
|
9 |
57,4 |
60,4038 |
-3,0038 |
|
10 |
67,6 |
64,8391 |
2,7609 |
|
11 |
63,9 |
68,4806 |
-4,5806 |
|
12 |
71,8 |
71,1533 |
0,6467 |
|
13 |
79,3 |
72,731 |
6,5690 |
|
14 |
81,3 |
73,1365 |
8,1635 |
|
15 |
59,6 |
72,3411 |
-12,7411 |
|
16 |
64,2 |
70,3652 |
-6,1652 |
|
17 |
67,9 |
67,2778 |
0,6222 |
|
18 |
78,8 |
63,197 |
15,6030 |
|
19 |
64,6 |
58,2893 |
6,3107 |
|
20 |
45,7 |
52,7705 |
-7,0705 |
|
21 |
41,0 |
46,9049 |
-5,9049 |
|
22 |
36,8 |
41,0058 |
-4,2058 |
|
23 |
33,9 |
35,4351 |
-1,5351 |
|
24 |
31,6 |
30,6037 |
0,9963 |
|
25 |
28,7 |
26,9714 |
1,7286 |
|
26 |
26,7 |
25,0466 |
1,6534 |
|
27 |
25,1 |
25,3867 |
-0,2867 |
|
28 |
29 |
28,5977 |
0,4023 |
|
29 |
39,7 |
35,3348 |
4,3652 |
|
30 |
42,4 |
46,3016 |
-3,9016 |
Приложение № 2
Polynomial Regression Analysis
-----------------------------------------------------------------------------
Dependent variable: Y
-----------------------------------------------------------------------------
Standard T
Parameter Estimate Error Statistic P-Value
-----------------------------------------------------------------------------
CONSTANT 37,8089 6,4945 5,82168 0,0000
t -6,05758 2,80081 -2,16279 0,0403
t^2 1,81869 0,359059 5,06515 0,0000
t^3 -0,114605 0,0172693 -6,63633 0,0000
t^4 0,00203425 0,000276526 7,35644 0,0000
-----------------------------------------------------------------------------
tтабл(0,05;25)=2,06
Analysis of Variance
-----------------------------------------------------------------------------
Source Sum of Squares Df Mean Square F-Ratio P-Value
-----------------------------------------------------------------------------
Model 7945,15 4 1986,29 60,19 0,0000
Residual 825,073 25 33,0029
-----------------------------------------------------------------------------
Total (Corr.) 8770,23 29
Fтабл(0,05;4;25)=2,76
R-squared = 90,5923 percent
R-squared (adjusted for d.f.) = 89,0871 percent
Standard Error of Est. = 5,74482
Mean absolute error = 3,80267
Durbin-Watson statistic = 1,70505
The StatAdvisor
---------------
The output shows the results of fitting a fourth order polynomial
model to describe the relationship between Y and t. The equation of
the fitted model is
Y = 37,8089-6,05758*t + 1,81869*t^2-0,114605*t^3 + 0,00203425*t^4
Since the P-value in the ANOVA table is less than 0.01, there is a
statistically significant relationship between Y and t at the 99%
confidence level.
The R-Squared statistic indicates that the model as fitted explains
90,5923% of the variability in Y. The adjusted R-squared statistic,
which is more suitable for comparing models with different numbers of
independent variables, is 89,0871%. The standard error of the
estimate shows the standard deviation of the residuals to be 5,74482.
This value can be used to construct prediction limits for new
observations by selecting the Forecasts option from the text menu.
The mean absolute error (MAE) of 3,80267 is the average value of the
residuals. The Durbin-Watson (DW) statistic tests the residuals to
determine if there is any significant correlation based on the order
in which they occur in your data file. Since the DW value is greater
than 1.4, there is probably not any serious autocorrelation in the
residuals.
In determining whether the order of the polynomial is appropriate,
note first that the P-value on the highest order term of the
polynomial equals 1,04666E-7. Since the P-value is less than 0.01,
the highest order term is statistically significant at the 99%
confidence level. Consequently, you probably don't want to consider
any model of lower order.
