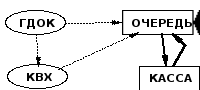
9. Одноканальная система массового обслуживания

П: Имеется кассовое окошко в банке, к которому выстраивается очередь из клиентов, на каждого из которых требуется различное время обслуживания. Как только касса освобождается, к нему подходит следующий клиент.

SWITCH –условный переключатель по нулю

Ф.Н=SWITCH(А.Н,В.Н,С.Н)

У КАССА.Н=WAIT(ОЧЕР.ПН)

Д ГДОК=WHOLE(RAND(O,5),0)

Д КВХ.Н=SWITCH(1,0,ГДОК.Н)

Д ДО.Н=LFIFO(ГДОК.Н,КВХ.Н,КАССА.Н,20,1)

Т ОЧЕР.НБ=FIFO(ГДОК.Н,КВХ.Н,КАССА.Н,20,1)

При имитации одноканальной СМО функции WAITиFIFOорганизуют контур, в результате которого появляется «холостой» ход между обслуживанием двух заявок. Для уничтожения «холостого» хода в последний шаг периода активности выходWAIT1, аWAIT=0,999 (т.е.WAITпопадает в режим открытие по ключу). Это позволяет на последнем шаге «периода активности» приоткрывать очередь и выбирать очередную заявку. Для компенсации 0,0001 в первом шаге «периода активности» выходWAIT=1,001. Для одиночных заявок выходWAIT=0,999.

Время	ГДОК	ОЧЕР	КАССА	ДО
0	3(3,25)	3	0	0
1	1(1,75)	0	1,001	1
2	1(1,25)	0	1	2
3	2(2,56)	1	0,999	2
4	4(4,06)	1	0,999	2
5	3(3,45)	2	0,999	2
6	1(1,63)	0	1,001	3
7	2(2,33)	4	0,999	3
8	3(3,45)		1,001	4
9	4(4,02)		1	5

10. Адаптация имитационной модели одноканальной смо

Адаптировать модель кассового окошечка блоком, определяющим для каждой заявки время от прихода заявки до поступления ее на обслуживающий элемент, при этом собственное время обслуживания не учитывается.

У КАССА.Н=WAIT(ОЧЕР.ПН)

* генератор длительности обслуживания клиентов

Д ГДОК.Н=WHOLE(RAND(0,5),0)

Д КВХ.Н=SWITCH(1,0,ГДОК.Н)

*очередь времен прихода клиентов

Д ОВПК.Н=FIFO(ВРЕМЯ,КВХ.Н,КАССА.Н,20,1)

*время простоя клиента

Д ВПК.Н=(ВРЕМЯ-ОВПК.Н)*SWITCH(0,1,ОВПК.Н)

Т ОЧЕР.НБ=FIFO(ГДОК.Н,КВХ.Н,КАССА.Н,20,2)

Очередь ОВПК, для которого используется, работает синхронно с очередью, но хода в очередь поступает заявка, выраженная в виде потенциального времени обслуживания, то одновременно в ОВПК поступает время прихода заявки. Когда регулирующие переменные КАССА выбирает из ОЧЕР числовое значение периода обслуживания заявки, то синхронно из ОВПК выходит время прихода этой заявки. Если из текущего времени вычесть время прихода заявки, то это будет время простоя заявки в очереди.

ОЧЕР- время обслуживания клиента

ОВПК- очередь, время прихода клиента

11. Имитация Марковского процесса / Имитация Марковских процессов

Адаптировать базовую модель склада блоком, в котором поступление описывается Марковским процессом с матрицей перехода

| 0,2 0,8 |

| 0,3 0,7 |

причем в первом состоянии поставляется 300 единиц, а во втором – 100. Выборка постоянна и равна 200.

* склад

У С.Н=С.П+ПОС.ПН-ВЫБ.ПН

* дополнительный уровень

У ДУ.Н=ДУ.П+ВХДУ.ПН-ВЫДУ.ПН

* входной темп дополнительного уровня

Т ВХДУ.НБ = (1-ДУ.Н)*EVENT(0,3)

* выходной темп дополнительного уровня

Т ВЫДУ.НБ=ДУ.Н*EVENT(0,8)

* поступление

Т ПОС.НБ=SWITH(100,300,ДУ.Н)

* выборка

Т ВЫБ.НБ=200

EVENT – событие

Ф.Н = EVENT(А.Н)

Ф(t) = 1 с вероятностьюA(t)

Ф(t) = 0 с вероятностью (1-A(t))