Лабораторная работа №1

по курсу "Компьютерная томография"

МОДЕЛИРОВАНИЕ ЗАШУМЛЕННЫХ ИЗОБРАЖЕНИЙ. ОЦЕНКА ВИЗУАЛЬНОГО КАЧЕСТВА ЦИФРОВЫХ

ИЗОБРАЖЕНИЙ. КРИТЕРИИ КАЧЕСТВА

Цель работы: исследование процесса искажения цифрового изображения, ознакомление с критериями оценки качества изображения, проведение оценки качества изображения, сравнительный анализ полученных оценок качества изображения в зависимости от наложенной на исходное изображение модели шума.

1. Модель процесса искажения изображения [1]

Как показано на Рис. 1, модель процесса ис­кажения изображения предполагает действие некоторого искажающего оператора на исходное изображение , что после добавления аддитивного шума дает искаженное изображение .

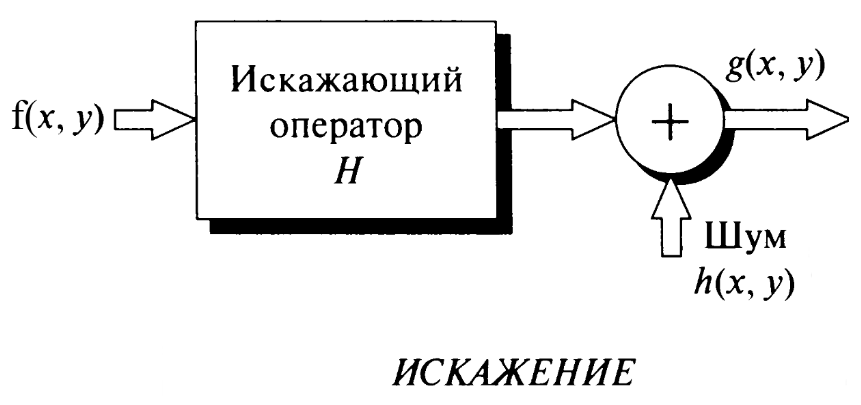
Рис. 1. Модель процесса искажения изображения

Искаженное изображение может быть представлено в пространственной области в виде:

,

где – функция, представляющая искажающий оператор в пространственной области, а символ «» используется для обозначения свертки.

Основные источники шума на цифровом изображении — это сам про­цесс его получения (оцифровки), а также процесс передачи. Работа сен­соров зависит от различных факторов, таких как внешние условия в процессе видеосъемки и качество сенсоров. Например, в процессе по­лучения изображения с помощью фотокамеры с ПЗС матрицей, основ­ными факторами, влияющими на величину шума, являются уровень освещенности и температура сенсоров. В процессе передачи изобра­жения могут искажаться помехами, возникающими в каналах связи.

Например, при передаче изображения с использованием беспровод­ной связи, оно может быть искажено в результате разряда молнии или других возмущений в атмосфере.

В рамках данной работы будем иметь дело с описанием поведения шума в пространственной об­ласти, которое основано на статистических свойствах значений ярко­сти компоненты шума в модели на Рис. 1. Эти значения яркости могут рассматриваться как случайные величины, характеризующиеся функцией плотности распределения вероятностей. Ниже даны приме­ры функций плотности распределения вероятностей, которые наибо­лее часто встречаются в приложениях, связанных с обработкой изоб­ражений.

Гауссов шум. Математическая простота, характерная для работы с моделями гауссова шума (также называемого нормальным шумом) как в пространствен­ной, так и в частотной области, обусловила широкое распростране­ние этих моделей на практике. На самом деле эта простота оказыва­ется столь привлекательной, что зачастую гауссовы модели используются даже в тех ситуациях, когда их применение оправда­но, в лучшем случае, лишь частично.

Функция плотности распределения вероятностей гауссовой слу­чайной величины задается выражением

, (1)

где представляет собой значение яркости, — среднее значение слу­чайной величины (математическое ожидание), — ее среднеквадратическое отклонение (СКО). Квад­рат среднеквадратического отклонения называется дисперсией ве­личины . График этой функции представлен на Рис. 2а.

Шум Релея. Функция плотности распределения вероятностей шума Релея задается выражением

(2)

Математическое ожидание и дисперсия для этого распределения имеют вид и .

График плотности распределения вероятностей шума Релея пред­ставлен на Рис. 2б. Обратите внимание на местоположение нача­ла координат и на то обстоятельство, что график имеет асимметричную (перекошенную вправо) форму. Распределение Релея бывает по­лезно для приближения асимметричных гистограмм.

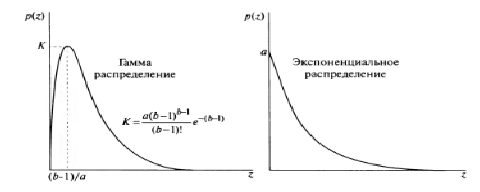
Рис. 2. Функции плотности распределения вероятностей

Шум Эрланга (гамма шум). Функция плотности распределения вероятностей шума Эрланга задается выражением

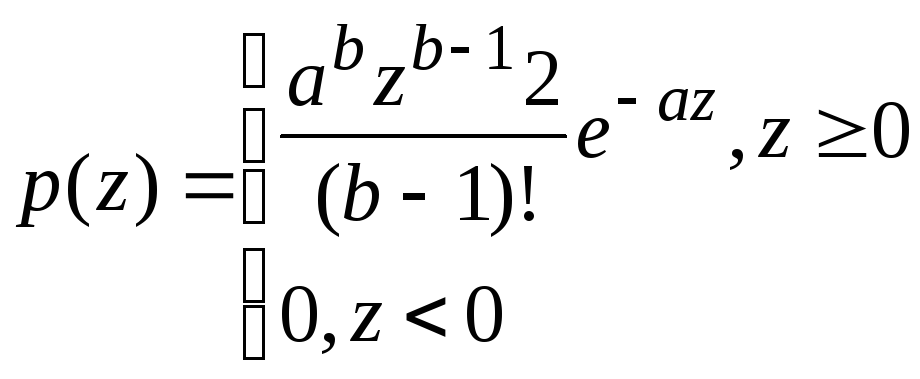, (3)

где , — положительное целое число и символ «!» обозначает факториал. Математическое ожидание и дисперсия для этого распределения имеют вид и .

На Рис. 2в представлен график плотности этого распределения. Выражение часто называют гамма распределением, хотя, стро­го говоря, это название относится к распределению более общего вида, когда не является целым, а в знаменателе стоит гамма-функ­ция . Рассматриваемый частный случай правильнее называть рас­пределением Эрланга.

Экспоненциальный шум. Функция плотности распределения вероятностей экспоненциального шума задается выражением

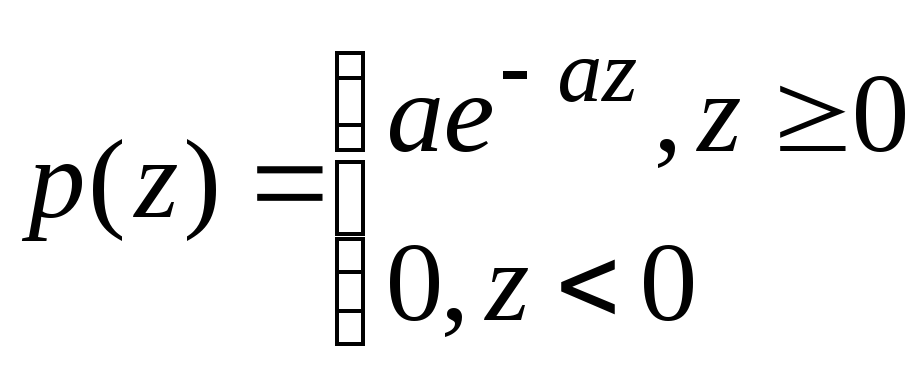, (4)

где . Среднее и дисперсия для этого распределения имеют вид и.

Заметим, что это распределение является частным случаем рас­пределения Эрланга с . На Рис. 2г представлен график плот­ности этого распределения.

Равномерный шум. Функция плотности распределения вероятностей равномерного шу­ма задается выражением

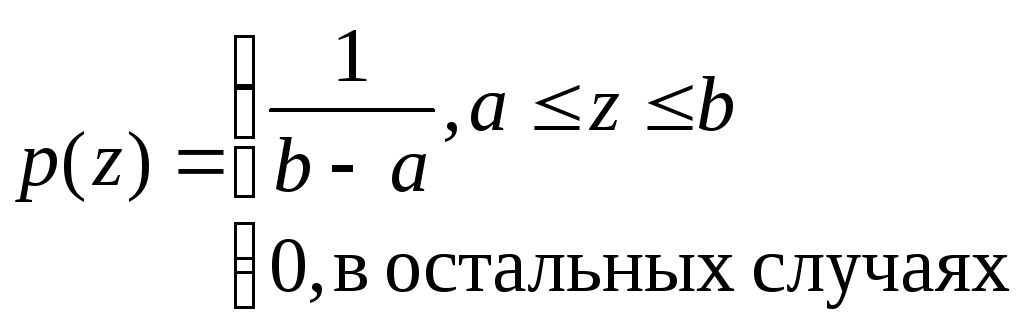, (5)

Среднее значение для этого распределения равно , а дисперсия .

На Рис. 2д представлен график плотности этого распределения.

Импульсный шум. Функция плотности распределения вероятностей (биполярного) импульсного шума задается выражением

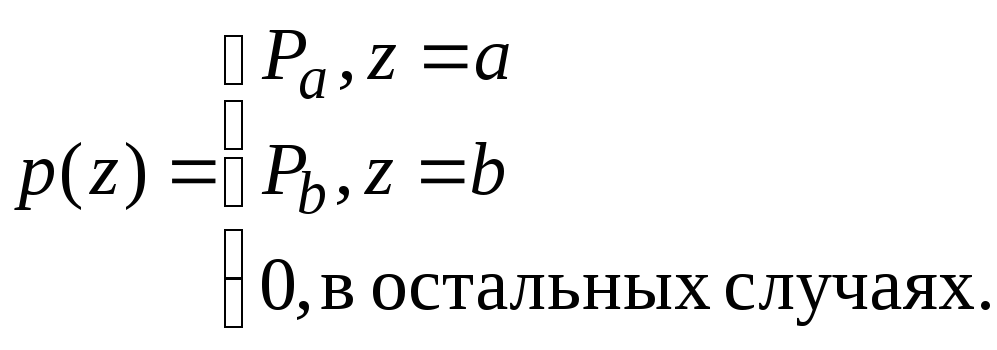(6)

Если , то пиксель с яркостью выглядит как светлая точка на изо­бражении. Пиксель с яркостью a выглядит, наоборот, как темная точ­ка. Если одно из значений вероятности (или ) равно нулю, то им­пульсный шум называется униполярным. Если ни одна из вероятностей не равна нулю, и в особенности если они приблизительно равны по величине, импульсный шум походит на крупицы соли и перца, слу­чайно рассыпанные по изображению. По этой причине импульсный шум называют также шумом типа «соль и перец».