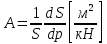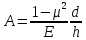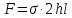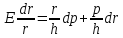Ткань кровеносных сосудов (сосудистая ткань)

Структура сосудистой стенки:

1) внутренний слой = интима = эндотелиальные клетки + подэндотелиальный слой;

2) средний слой = концентрические эластические оболочки с волокнами одного направления + гладкомышечные клетки между ними;

3) наружная оболочка = адвентиция = крупные пучки эластичных волокон с поперечными связями;

4) эластичная базальная мембрана = толстые эластичные волокна, расположенные вдоль сосуда + коллагеновые волокна по окружности сосуда + поперечные связи.

Рис.7.4. Зависимость напряжения σ стенок кровеносных сосудов от величины деформации ε.

Механические свойства кровеносных сосудов определяются главным образом свойствами коллагена, эластина и гладких мышечных волокон. Содержание этих составляющих сосудистой ткани изменяется по ходу кровеносной системы: отношение эластина к коллагену в общей сонной артерии – 2:1, а в бедренной артерии – 1:2. С удалением от сердца увеличивается доля гладких мышечных волокон, в артериолах они уже являются основной составляющей сосудистой ткани. Общая зависимость напряжения σ стенок кровеносных сосудов от величины деформации ε представлена на рис.7.4.

В физиологических условиях ткани кровеносных сосудов представляют собой нелинейный упругий малосжимаемый анизотропный материал. При этом механические свойства стенки определяются главным образом свойствами средней сосудистой оболочки, состоящей из коллагена, эластина и гладких мышечных волокон. При низком давлении решающую роль в процессе деформирования играют волокна эластина, при физиологическом давлении – эластина и коллагена, при высоком давлении – коллагена.

Для артериальных сосудов модуль упругости Е изменяется в широких пределах: от 0,06 до 0,7 МПа. Это связано с тем, что под влиянием нервных и химических воздействий клетки гладких мышечных волокон сокращаются. Благодаря сокращению гладких мышц изменяются размеры кровеносных сосудов и их механические свойства. Если до сокращения мышечных волокон модуль упругости Е=0,01 МПа, то при сокращении (стимуляции) Е=0,1 МПа.

С увеличением расстояния от сердца предельная деформация, соответствующая разрыву стенки артерий, уменьшается. Наибольшую прочность имеет общая сонная артерия (предел прочности в осевом направлении σ=2 МПа, предельная деформация ε=0,61).

С возрастом жёсткость стенок увеличивается, а прочность уменьшается.

Для оценки жёсткости стенки можно воспользоваться расчётной схемой тонкостенной цилиндрической оболочки с использованием параметра A, называемого характеристикой растяжимости. Растяжимость – величина, обратная жёсткости, – определяет общее перемещение под действием суммарной единичной силы. Для стенок кровеносных сосудов растяжимость характеризуется изменением объёма в зависимости от давления. Характеристика растяжимости стенки определяется формулой:

,

(7.2.2)

где: S – площадь отверстия (просвета сосуда), р – избыточное давление.

Если материал стенки изотропный, то величина A может быть рассчитана по формуле:

,

(7.2.3)

где: Е – модель упругости, μ – коэффициент Пуассона (для несжимаемого материала μ=0,5), d – средний диаметр стенки, h – средняя толщина стенки.

Упругость артериальных стенок обусловлена наличием в них эластина. В грудной аорте содержание эластина достигает 30% от сухой массы стенки, в брюшной аорте и других артериях – до 15%.

Деформацию сосуда в целом можно рассматривать как результат действия давления изнутри на упругий цилиндр.

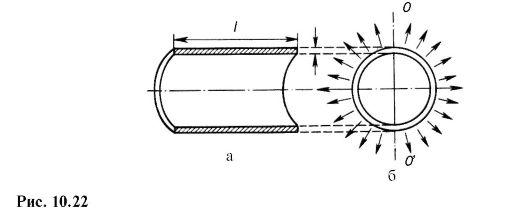
Рассмотрим цилиндрическую часть кровеносного сосуда длиной l, с толщиной стенок h и радиусом внутренней части r. Сечения вдоль и поперек оси цилиндра показаны на рис.7.5. Две половины цилиндрического сосуда взаимодействуют между собой по сечениям стенок цилиндра (заштрихованные области на рис.7.5,а).

Общая площадь этого «сечения взаимодействия» равна 2hl. Если в сосудистой стенке существует механическое напряжение σ, то сила взаимодействия двух половинок сосуда равна:

.

(7.2.1)

Эта сила уравновешивает силы давления на цилиндр изнутри (они показаны стрелками на рис. 7.5,б).

Рис. 7.5. Сечения цилиндрического сосуда вдоль продольной оси (а) и поперёк оси (б).

Силы направлены под разными углами к горизонтальной плоскости (на рисунке). Для того чтобы найти их равнодействующую, следует просуммировать горизонтальные или вертикальные проекции. Проекцией в этом случае будет прямоугольник, одна сторона которого – это длина сосуда l, а друга – внутренний диаметр сосуда d=2r. Тогда равнодействующая сила давления жидкости будет иметь вид:

.

(7.2.2)

Приравнивая (7.2.1) и (7.2.2), получаем , откуда:

.

(7.2.3)

Это уравнение Ламе.

Из (7.2.3) видно что в капиллярах (r→0) напряжение почти отсутствует (σ→0).

Формула (7.2.3) выражает зависимость четырёх величин, и поэтому установить некоторые зависимости с помощью этой формулы затруднительно. Кроме того, уравнение (7.2.3) не включает модуль упругости – основную механическую характеристику упругого тела, поэтому целесообразно преобразовать эту формулу в каком-либо приближённом варианте. Например, попытаться найти зависимость p=f(r).

Продифференцируем (7.2.3) как функцию двух переменных (σ=f(p,r):

.

(7.2.4)

Продифференцирован уравнение Гука (σ=Eε), получим:

.

(7.2.5)

Применительно к цилиндрическому сосуду элементарное изменение относительной деформации можно представить следующим образом:

.

(7.2.6)

Подставляя (7.2.6) в (7.2.5) получим:

.

(7.2.7)

Приравнивая (7.2.4) и (7.2.7), находим:

.

(7.2.8)

Преобразуем это уравнение:

.

(7.2.9)

Если Е велико, а r мало, то тогда , и можно получить приближённую формулу:

.

(7.2.10)

Уравнения (7.2.9) и (7.2.10) могут быть использованы для нахождения связи между давлением и радиусом кровеносного сосуда, а также модуля упругости. При решении вопроса о распространении пульсовой волны количественные соотношения получаются также на основе этих уравнений (формула (7.11), лекция 7, часть 1).

Как правило, в стенках артерий больше эластичных волокон и меньше коллагеновых, чем в стенках вен. Вены же, напротив, более богаты коллагеновыми волокнами. Капилляры имеют эндотелиальный слой, но их стенки лишены мышечной и соединительной ткани. Они относительно пассивны, и их поведение определяется преимущественно процессами, происходящими в примыкающих артериолах и венулах. Лимфатические сосуды по строению сходны с венами, но отличаются от них меньшей толщиной и большей проницаемостью.