Контрольные вопросы Вариант 1 (нечётные порядковые номера в списке группы)

1. Метод Гаусса для решения систем линейных уравнений реализуем:

   1. всегда;

   2. если главный определитель системы не равен нулю;

   3. если все элементы главной диагонали матрицы коэффициентов левых частей уравнения, изменяемой на каждом шаге прямого хода метода, не равны нулю.

2. Метод прогонки для решения систем линейных уравнений:

   1. относится к прямым;

   2. относится к итерационным;

   3. не относится ни к тем, ни к другим.

3. Многочлен 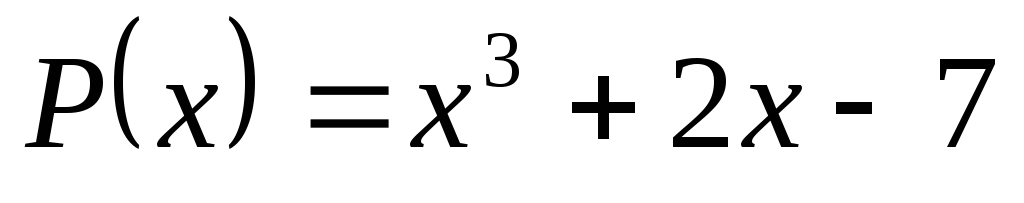имеет действительный корень на интервале:

   1. (-1; 0);

   2. (0; 1);

   3. (1; 2);

   4. на другом интервале.

4. Для приближенного решения уравнения f(x)=0 подобрали отрезок [a;b], на котором находится решение. Тогда формулареализует:

   1. метод половинного деления;

   2. метод хорд;

   3. метод Ньютона (касательных).

5. Функция f(x) имеет график, вид которого показан на рисунке.

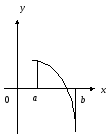
Ищется корень этой функции методом Ньютона. Тогда в качестве начального приближения корня:

1. можно взять a;

2. можно взять b;

3. нельзя взять ни a, ниb.

1. Даны 2 последовательности:

x	2	4	6
y	-4	8	28

Тогда значением сплайна первого порядка, построенного на этих последовательностях, при x=5, будет:

1. 16;

2. 18;

3. 20.

1. У многочлена Чебышева степени 3 коэффициент при старшей степени переменной равен:

   1. 3;

   2. 4;

   3. 8;

   4. 9.

2. По числовым последовательностям xиyпостроили график, показанный на рисунке.

Тогда для них наилучшим образом подойдет:

1. линейный тренд;

2. показательный тренд;

3. полиномиальный тренд.

1. Аппроксимация имеет погрешность порядка:

   1. h;

   2. h²;

   3. h³.

2. Формула для приближенного вычисления определенного интеграла с помощью разбиения отрезка интегрированияявляется формулой:

   1. левых прямоугольников;

   2. правых прямоугольников;

   3. средних прямоугольников;

   4. трапеций;

   5. Симпсона.

3. Локальная погрешность формулы Симпсона пропорциональна:

   1. h;

   2. h²;

   3. h³;

   4. h⁴;

   5. h⁵.

4. Для приближенного решения задачи Коши для обыкновенного дифференциального уравнения первого порядка y’=f(x,y) применена формула. Тогда эта формула реализует:

   1. явный метод Эйлера;

   2. явный метод Рунге-Кутта;

   3. другой метод.

5. Глобальная погрешность явного метода Эйлера пропорциональна:

   1. h;

   2. h²;

   3. h³.

6. Дан числовой ряд . Тогда:

   1. для приближенного вычисления его суммы с точностью до 0,001 достаточно взять 1000 слагаемых;

   2. для приближенного вычисления его суммы с точностью до 0,001 достаточно взять 100 слагаемых;

   3. для приближенного вычисления его суммы с точностью до 0,001 достаточно взять 10 слагаемых;

   4. приближенное вычисление его суммы не имеет смысла, поскольку он расходится.

Вариант 2 (чётные порядковые номера в списке группы)

1. Обратная матрица существует:

   1. у любой квадратной матрицы;

   2. у квадратной матрицы, определитель которой не равен нулю;

   3. у любой матрицы, не обязательно квадратной.

2. Метод Зейделя для решения систем линейных уравнений:

   1. относится к прямым;

   2. относится к итерационным;

   3. не относится ни к тем, ни к другим.

3. Многочлен имеет действительный корень на интервале:

   1. (-2; -1);

   2. (-1; 0);

   3. (0; 1);

   4. на другом интервале.

4. Для приближенного решения уравнения f(x)=0 подобрали отрезок [a;b], на котором находится решение. Тогда на этом интервале:

   1. график функции f(x) должен пересечь ось абсцисс ровно один раз;

   2. график функции f(x) может пересечь ось абсцисс сколь угодно много раз;

   3. график функции f(x) не обязан пересекать ось абсцисс.

5. Функция f(x) имеет график, вид которого показан на рисунке.

Ищется корень этой функции методом Ньютона. Тогда в качестве начального приближения корня:

1. можно взять a;

2. можно взять b;

3. нельзя взять ни a, ниb.

1. Даны 2 последовательности:

x	1	3	5
y	4	12	28

Тогда значением сплайна первого порядка, построенного на этих последовательностях, при x=2, будет:

1. 7;

2. 8;

3. 9.

1. Многочлен Чебышева степени n:

   1. имеет ровно nдействительных различных корней;

   2. имеет ровно nразличных корней, среди которых могут быть комплексные;

   3. может иметь кратные корни.

2. По числовым последовательностям xиyпостроили график, показанный на рисунке.

Тогда для них наилучшим образом подойдет:

1. линейный тренд;

2. показательный тренд;

3. полиномиальный тренд.

1. Аппроксимация имеет погрешность порядка:

   1. h;

   2. h²;

   3. h³.

2. Формула для приближенного вычисления определенного интеграла с помощью разбиения отрезка интегрирования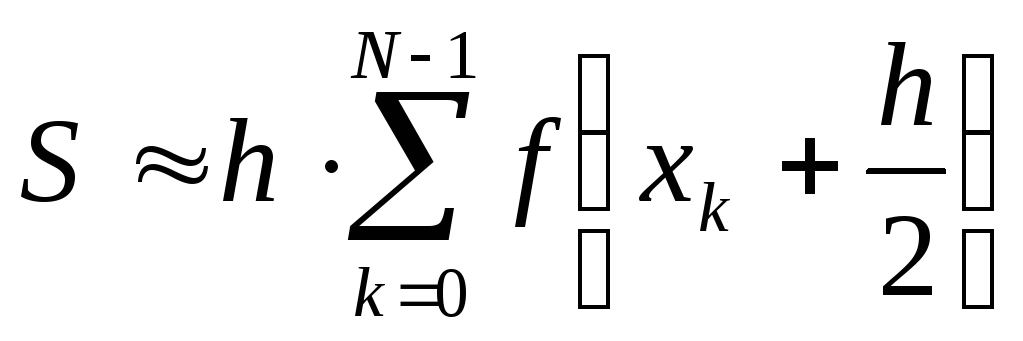является формулой:

   1. левых прямоугольников;

   2. правых прямоугольников;

   3. средних прямоугольников;

   4. трапеций;

   5. Симпсона.

3. Глобальная погрешность формулы Симпсона пропорциональна:

   1. h;

   2. h²;

   3. h³;

   4. h⁴;

   5. h⁵.

4. Задача y’’=x+y+y’,y(0)=0,y(1)=1 является:

   1. задачей Коши;

   2. краевой задачей;

   3. ни той, ни другой.

5. Пусть для приближенного задачи Коши для обыкновенного дифференциального уравнения применен какой-либо метод с локальной погрешностью, пропорциональной h^p. Тогда глобальная погрешность этого же метода будет пропорциональна:

   1. h^p-1;

   2. h^p;

   3. h^p+1.

6. Дан числовой ряд . Тогда:

   1. для приближенного вычисления его суммы с точностью до 0,001 достаточно взять 1000 слагаемых;

   2. для приближенного вычисления его суммы с точностью до 0,001 достаточно взять 100 слагаемых;

   3. для приближенного вычисления его суммы с точностью до 0,001 достаточно взять 10 слагаемых;

   4. приближенное вычисление его суммы не имеет смысла, поскольку он расходится.