Классический метод расчета переходных

процессов в линейных цепях.

ЗАКОНЫ КОММУТАЦИИ.

Внезапное изменение токов и/или напряжений или внезапное изменение

параметров цепи называется коммутацией.

В чисто резистивных цепях не происходит никаких накоплений энергии,

поэтому режим устанавливается мгновенно вслед за коммутацией.

В цепях, содержащих реактивные элементы, требуется время для изменения запасенных энергий (теоретически ¥).

Для мгновенного изменения энергий требуется бесконечно большие мощности

Поскольку и ограничены, следовательно:

1. 2.

1. В любой ветви с индуктивностью ток и магнитный поток в момент коммутации сохраняют те значения, которые они имели до коммутации и их изменения начинаются с этих значений.

2. Напряжение и заряд на емкости сохраняют в момент коммутации те значения, которые они имели до коммутации и их изменения начинаются с этих значений.

Теоретически можно представить мгновенное

изменение тока через индуктивность, однако

это потребует бесконечно большого напряже-

ния.

Аналогично, для мгновенного изменения на-

пряжения на емкости требуется источник с

бесконечно большим током.

Таким образом, при коммутации допускаются изменения

Необходимо учитывать идеализацию, связанную с бестоковой коммутацией.

ПОРЯДОК РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ КЛАССИЧЕСКИМ МЕТОДОМ.

Дифференциальные уравнения по законам Кирхгофа записываются без всяких изменений и ограничений по законам коммутации и по формам сигналов, поэтому они описывают соотношения в цепях при переходных процессах.

Например, для последовательного RLC контура:

d i 1 to

u(t) = R * i + L * ----- + --- ò [i(t) d t] или

d t C 0

То же самое уравнение справедливо и для установившегося процесса:

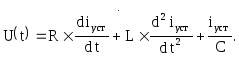
Назовем свободным током разность между истинным переходным током и установившимся:

Вычитаем одно уравнение из другого:

Свободный ток определяется только параметрами самой цепи.

Физически существует только ток i . Поскольку разделение и последующее сложение токов основывается на принципе суперпозиции, то этот прием применим лишь к линейным цепям.

Разложение соответствует математическому приему: решение неоднородного диф. ур. определяется как сумма частного решения неоднородного диф. ур. и общего решения однородного диф. ур.

В общем случае из системы уравнений по законам Кирхгофа для тока в

k-й ветви можно получить:

Решение этого уравнения:

где - корни характеристического уравнения:

Для приведенного примера:

– определяется из начальных условий.

КОРОТКОЕ ЗАМЫКАНИЕ RL ЦЕПИ.

R₀ R

E

L

В момент времени t = 0 ключ замыкается. Ток в цепи до коммутации

E/(R₀+R). Требуется определить ток после коммутации.

Уравнение по закону Кирхгофа:

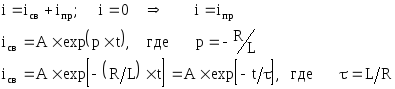
По закону коммутации:

Если бы в цепи протекал переменный ток, то в решении изменится только

A = i(0-).

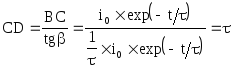
Таким образом, для любой точки проекция касательной в этой точке на ось времени есть величина постоянная const = t.

b

C t D t

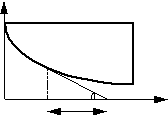
Энергия, рассеиваемая в сопротивлении:

– равна энергии, запасенной в индуктивности.

ВКЛЮЧЕНИЕ RL ЦЕПИ НА ПОСТОЯННОЕ НАПРЯЖЕНИЕ.

R

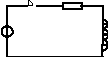E L Решение:

Однородное уравнение:

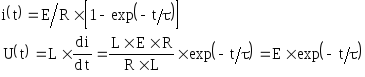
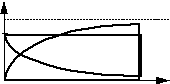i U_L

E i_L i t одно и то же

U_L t

ВКЛЮЧЕНИЕ RL ЦЕПИ НА СИНУСОИДАЛЬНОЕ НАПРЯЖЕНИЕ.

принужденный ток: свободный ток:

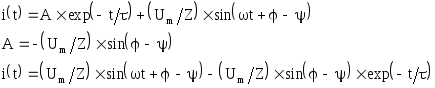
i ¬ i_пр

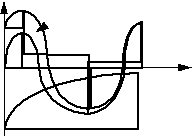i

t

­

i_св

1. j - y = 0 – свободная составляющая отсутствует. В цепи сразу возникает установившийся ток.

2. j - y = p / 2 и t ® ¥, то через т / 2 ток в катушке индуктивности превышает амплитудное значение в 2 раза: i_max £ 2I_{m уст}.

ВКЛЮЧЕНИЕ RC ЦЕПИ НА ПОСТОЯННОЕ НАПРЯЖЕНИЕ.

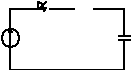
R

E C

Решение:

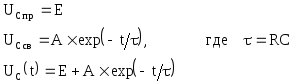
Из начальных условий U_C(0-) = U_C(0+) = 0

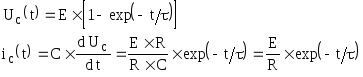
Значение тока в момент включения соответствует накоротко замкнутой ёмкости.

ПЕРЕХОДНЫЕ ПРОЦЕССЫ ПРИ МГНОВЕННОМ ИЗМЕНЕНИИ ПАРАМЕТРОВ ЦЕПИ.

Задача решается по такой схеме:

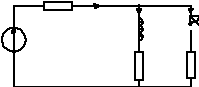
i i₁ i₂

R₁

E L

r R₂

1. Составляются диф. ур.

2. Решаем диф. ур.

3. Определяем постоянные интегрирования из законов коммутации.

Например, для схемы требуется найти токи

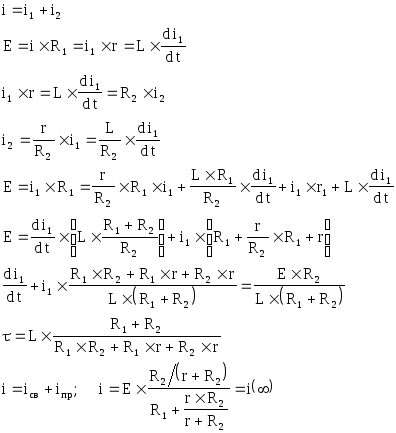
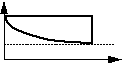
i(0)

i(¥)

t

Переходные процессы при мгновенном изменении параметров цепи (L или C).

Диф. уравнение (схему см. ниже):

Его решение:

R₁ L₁

E R₂

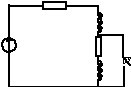
L₂

Однако применение закона коммутации для определения постоянной интегрирования встречает трудности. Это задача с некорректными начальными условиями. Здесь при идеализации задачи предполагаем, что в момент коммутации ток изменяется скачком. Напряжения на индуктивностях будут равны бесконечности при конечном напряжении источника питания. Поэтому приходим к выводу, что напряжения на индуктивностях должны быть равны по величине и противоположны по знаку:

Интегрируем полученное выражение в пределах [0-; 0+]

До коммутации:

После коммутации:

Следовательно:

С другой стороны:

Окончательно:

При определенных соотношениях может быть A = 0:

.

То есть новое установившееся значение тока получаем сразу после коммутации. Если сделать катушку с изоляцией, способной выдержать большое перенапряжение, то простым устройством можно менять ток в индуктивности.

РАЗРЯД КОНДЕНСАТОРА НА RL ЦЕПЬ.

R Уравнение:

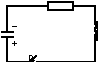U₀ L или:

Составляем характеристическое уравнение: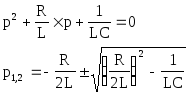

Установившийся режим нулевой, поэтому:

Постоянные интегрирования находятся из условий:

i (0-) = i (0+) Þ A₁ + A₂ = 0

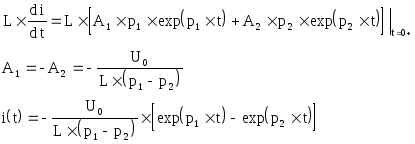
Напряжение на индуктивности:

Напряжение на активном сопротивлении:

Напряжение на емкости:

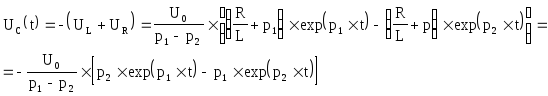Возможные варианты этих зависимостей определяют корни характеристического уравнения:

I. Корни вещественные и различны.

II. Корни вещественные и равны.

III. Корни комплексные.

I. Апериодический разряд:

При этом: p₁ < 0 и p₂ < 0; ïp₂ï > ïp₁ï

Следовательно:

Значит:

1. Ток не меняет своего направления.

2. При U₀ > 0 i < 0.

3. Конденсатор все время разряжается, т.е. U_С > 0.

4. Поскольку ток не меняет своего направления, должен быть максимум.

I_max находят из условия: d i / d t = 0. В это время напряжение на индуктивности равно нулю.

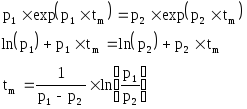
5. U_max находится из условия:

Следовательно:

II. Предельный случай апериодического разряда.

Выражение для тока становится неопределенным:

Для раскрытия неопределенности рассмотрим предел полученного выражения при:

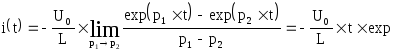
При кратных корнях всегда приходится раскрывать неопределенность.

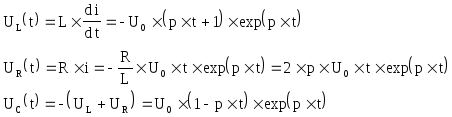
t_m можно найти из условия: U = 0. Откуда t_m = - 1 / p.

Кривые токов и напряжений своей формы не изменяют.

III. Периодический разряд.

Введем обозначения:

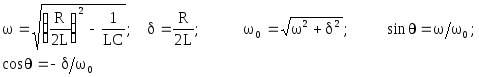
Тогда в случае можно записать

Тогда в данных обозначениях можно записать выражение для тока:

Используя формулу Эйлера можно получить:

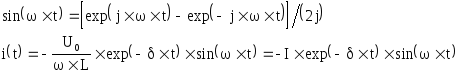
Таким образом, имеем затухающий колебательный процесс. Напряжение на индуктивности:

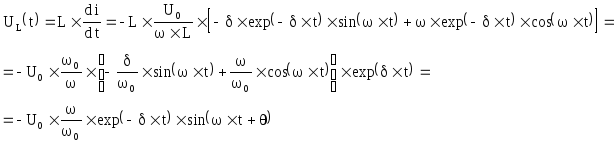Поскольку .

Напряжение на емкости:

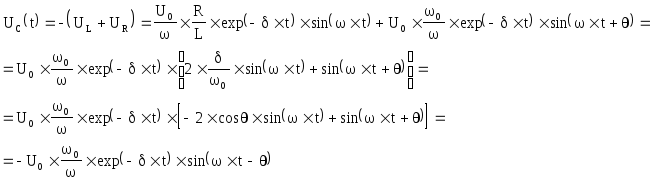используя, что

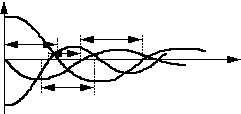
1. Строим ток i(t).

2. 

3. 

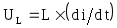
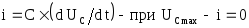
4. Угол q - угол между нулём тока и нулём U_C.

U₀ U_R

q q

q

i t

2p

U_L q

В предельном случае R=0; d=0; q = p/2.

U₀ U_R

t

i

-U₀ U_L

ВКЛЮЧЕНИЕ RLC ЦЕПИ.

L

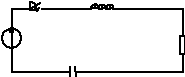
U(t) R

C

Уравнение: или

Решение:

Установившийся режим нулевой: i_уст = 0, поэтому:

Результат аналогичен полученному ранее, за исключением знака. В этом случае:

Напряжение на индуктивности:

Напряжение на активном сопротивлении:

Напряжение на ёмкости:

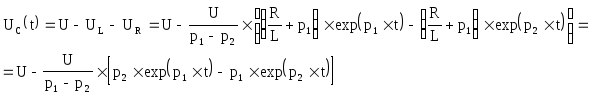
i , U U_C

i_L

t

i , U

U

i_L t

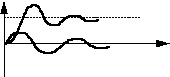
Пусть

Как и ранее

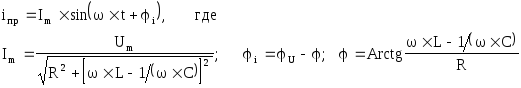Для нахождения постоянных интегрирования составим два уравнения:

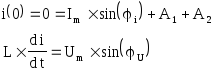
Из этих уравнений модно получить постоянные интегрирования A₁ и A₂:

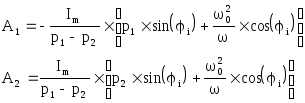
Выражение для тока в случае комплексных корней будет иметь вид:

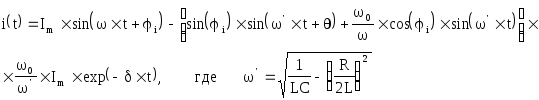Детальный анализ достаточно сложен. Например, если w = w` » w₀, т.е. d << w₀ и q = p / 2. Данные соотношения справедливы для случая, когда контур с малым затуханием включается на напряжение с частотой, равной собственной частоте. Тогда:

i

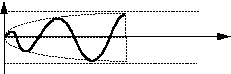
t

Ток изменяется по синусоидальному закону с амплитудой, возрастающей по экспоненте. Если частоты w и w` близки друг к другу, то

В первые периоды близко к 1. Тогда

- это биения колебаний.