Московский Государственный Институт Электронной Техники

(Технический Университет)

Кафедра Высшей Математики - I

КУРСОВАЯ РАБОТА

по “Методам прикладной математики”

на тему

“Приближённое решение краевых задач математической физики методом сеток.”

Выполнил: студент группы МП-35 Забродский Е.И.

Руководитель: Лесин В.В.

Москва, 2000 год.

1. Методические указания и постановка задачи.

1. Тема.

Приближенное решение краевых задач математической физики методом сеток.

1.1 Цель работы.

Изучить основные понятия теории конечно-разностных методов решения краевых задач математической физики и уметь применять их на практике. Численное решение задачи осуществляется на персональной ЭВМ в среде MATLAB. Преимущество использования этой cреды — богатый набор командных программ, реализующих большинство стандартных задач линейной алгебры и методов оптимизации, а также статистической обработки результатов. MATLAB обладает также хорошими графическими возможностями отображения результатов.

1.2 Порядок работы.

1. Познакомиться с основными понятиями метода сеток и методикой численного решения разностных уравнений, аппроксимирующих краевую задачу. Наиболее полно все основные понятия метода сеток изложены в [1,2]. Достаточной теоретической базой может служить методическое пособие [3].

2. Классифицировать уравнение и проверить корректность постановки данной в варианте краевой задачи и соответствие её физическому смыслу.

3. Разобраться с методикой построения явных и неявных разностных схем конечно-разностных систем для данного типа уравнения.

4. Разобраться с устойчивыми методами решения явной и неявной схем.

5. Реализовать программу, осуществляющую решение в среде MATLAB.

6. Получить численные результаты для своего варианта. Оформить их в виде таблиц, построить необходимые кривые и поверхности уровней, иллюстрирующие решение задачи.

7. Оформить курсовую работу в соответствии с общим требованиями к курсовым работам. В теоретической части должны быть кратко освещены следующие вопросы:

• Классификация уравнения. Вскрыть физический смысл тех явлений, которые описываются данной математической постановкой задачи.

• Корректная постановка: граничные и начальные условия и их соответствие физическому смыслу.

• Понятия: сеточный шаблон, порядок аппроксимации разностных схем, сходимость, устойчивость решения.

• Выбор шагов сетки и оценка погрешности метода.

2. Выполнение работы.

2.1. Классификация краевой задачи и её физический смысл

Основное уравнение:

Начальные условия:

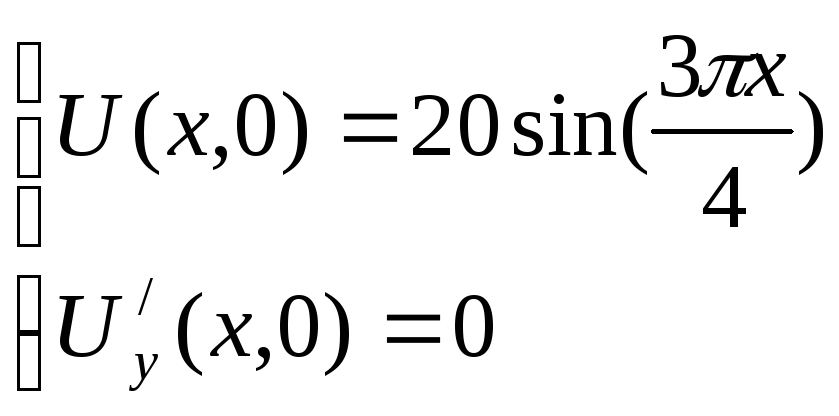
Граничные условия :

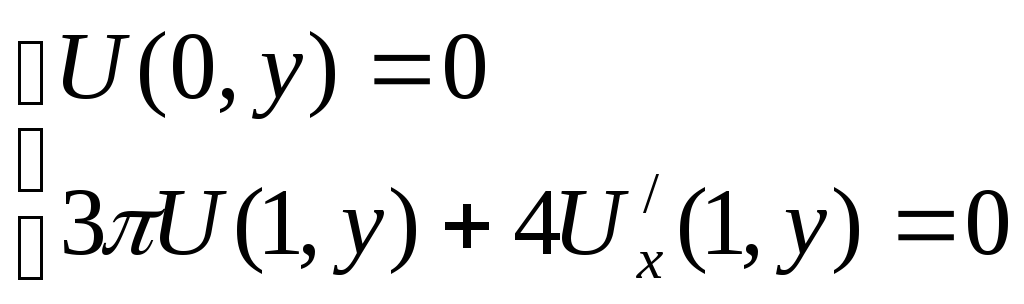
Линейное дифференциальное уравнение второго порядка такого вида относится к уравнениям гиперболического типа. Данное уравнение описывает процесс вынужденных колебаний струны. Рассмотрим струну длиной 1, закрепленную в точках x=0 и x=1. Положение каждой точки струны характеризуется значением координаты x. Пусть U=U(x,t) – вертикальное отклонение струны в точке x в момент времени t от положения равновесия. Так как концы струны закреплены, то

в любой момент времени должны выполняться граничные условия:

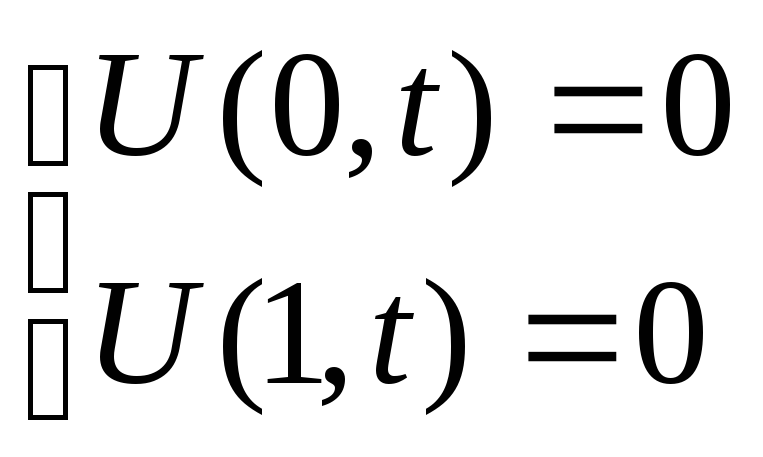
Процесс колебания струны зависит от ее начальной формы и от распределения

скоростей, поэтому задаются начальные условия:

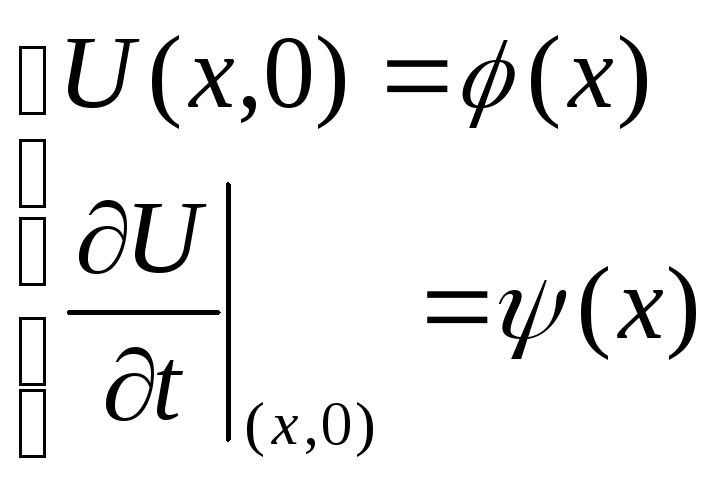
Начальные и граничные условия определяют решение уравнения колебаний

струны.

,

где

,

- натяжение струны, - плотность материала струны,- плотность внешней силы, расчитанная на единицу материала струны.

Если

,

то колебания будут свободными и затухающими. Если концы струны движутся по

заданному закону, то граничные условия принимают вид

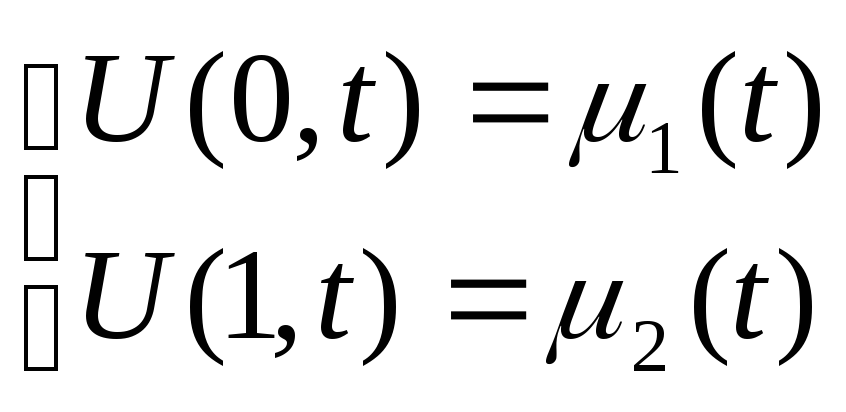
Возможны также и другие типы граничных условий. Итак, первая краевая задача для

уравнения колебаний струны ставится следующим образом:

Найти функцию, определенную в области,

удовлетворяющую уравнению

,

а так же граничным условиям

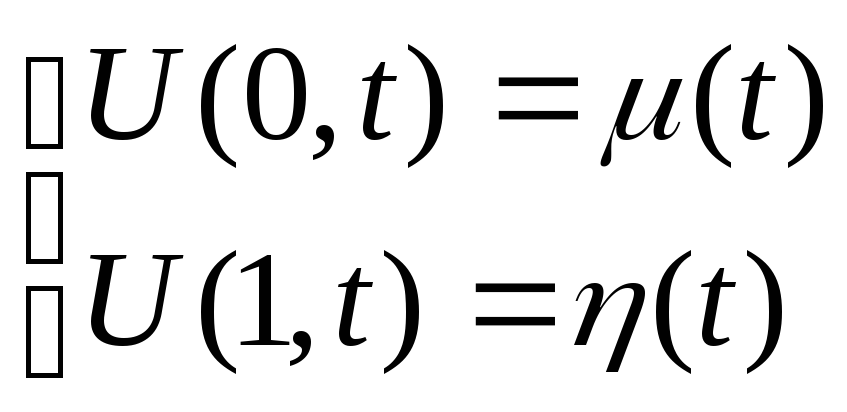
и начальным условиям

,

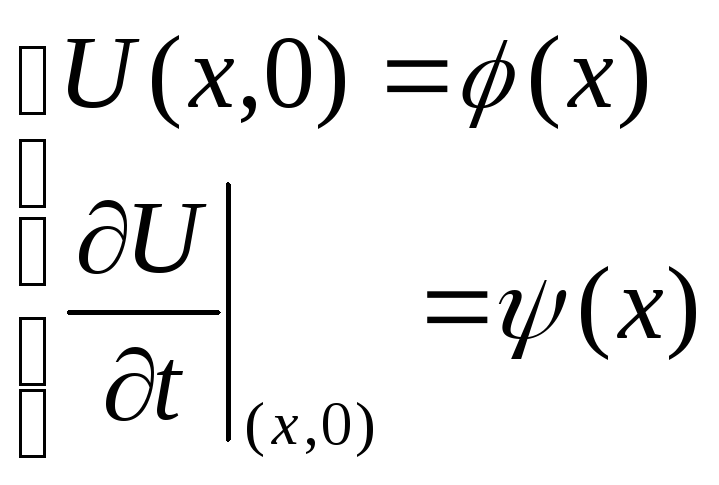где - заданные функции, -известная постоянная.

Метод сеток состоит в сведении решения краевой задачи к решению системы алгебраических уравнений для так называемой «сеточной функции». Для этого область G непрерывного изменения аргумента заменяется областью дискретного его изменения. Дифференциальный оператор заменяется некоторым разностным оператором. Краевые и начальные условия заменяются на соответствующие разностные аналоги.

Выберем в области, где ищется решение дифференциального уравнения, некоторое конечное множество точек, в которых мы будем искать решение уравнения. Ясно, что чем больше мы возьмем таких точек, тем точнее решим уравнение. Множество таких точек называется сеткой, отдельные точки - узлами сетки. Функция, определенная в узлах сетки , называется сеточной функцией.

Пусть дан линейный дифференциальный оператор L , действующий на функцию x . Заменяя входящими в L производные разностными отношениями, получим вместо L разностное выражение L_h_h являющееся линейной комбинацией значений сеточной функции _h на некотором множестве узлов сетки, называемом сеточным шаблоном. Такая приближенная замена L на L_h_h называется аппроксимацией дифференциального оператора разностным оператором.

Говорят, что L_h апроксимирует дифференциальный оператор L с

порядком аппроксимации m>0 в точке x, если