
- •Московский институт электронной техники (Технический университет)
- •Курсовая работа
- •Постановка задачи и её физическая интерпретация.
- •Применение метода сеток при решении уравнения Пуассона.
- •Реализация метода сеток на эвм в среде Matlab.
- •Приложение. Текст основной программы pavel.M.
- •Подпрограммаpav_eps.M определения погрешности при заданном параметре сходимости.
- •Подпрограммаpav_p.M доказывающая сходимость разностной схемы.
- •Литература.
Реализация метода сеток на эвм в среде Matlab.
Будем решать
данную систему методом верхней релаксации,
который является обобщением метода
Зайделя. (Метод верхней релаксации
вырождается в метод Зайделя при параметре
сходимости![]() .)
.)
Применительно к нашей конечно-разностной схеме, метод верхней релаксации записывается в виде:

Данный метод реализован в программе pavel.m (см. Приложение).
Итерационный процесс
сходится для всех
![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству![]() .
Вопрос о выборе оптимального значения
.
Вопрос о выборе оптимального значения![]() из данного промежутка, которое обеспечивало
бы максимальную скорость сходимости
метода верхней релаксации очень сложен
в теоретическом отношении. Но применительно
к конкретной задаче оптимальное значение
параметра сходимости можно определить
из машинного эксперимента. Автором была
написана программаpav_eps.m
(см. Приложние) в средеMatlab для изучения скорости
сходимости в зависимости от параметра
сходимости. За основу алгоритма было
взято решение данного уравнения на
сетке фиксированного размера за
фиксированное число шагов была получена
зависимость погрешности (которую можно
связать с величиной, обратной скорости
сходимости) от параметра сходимости
из данного промежутка, которое обеспечивало
бы максимальную скорость сходимости
метода верхней релаксации очень сложен
в теоретическом отношении. Но применительно
к конкретной задаче оптимальное значение
параметра сходимости можно определить
из машинного эксперимента. Автором была
написана программаpav_eps.m
(см. Приложние) в средеMatlab для изучения скорости
сходимости в зависимости от параметра
сходимости. За основу алгоритма было
взято решение данного уравнения на
сетке фиксированного размера за
фиксированное число шагов была получена
зависимость погрешности (которую можно
связать с величиной, обратной скорости
сходимости) от параметра сходимости![]() .
Графики этой функции на различных
интервалах представлены на рисунках.
.
Графики этой функции на различных
интервалах представлены на рисунках.

Таким образом было
получено оптимальное значение параметра
сходимости![]() .
Это значение и использовалось автором
при конечных вычислениях в программеpavel.m. График найденой
функции и её лини уровня представлены
на рисунках.
.
Это значение и использовалось автором
при конечных вычислениях в программеpavel.m. График найденой
функции и её лини уровня представлены
на рисунках.


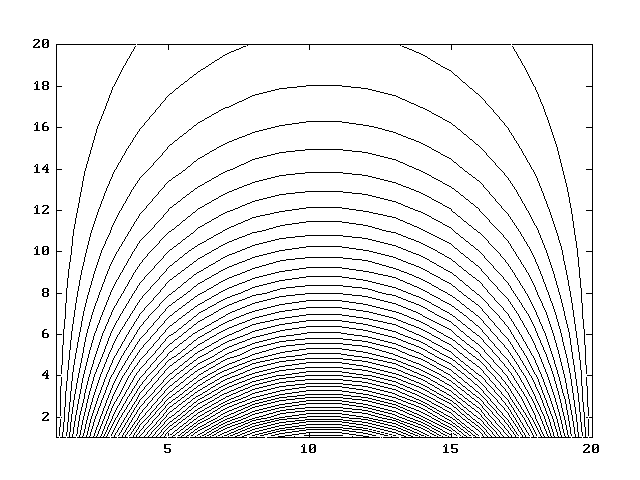
Матрица решения
заданного уравнения для M=N=10,
![]() приведена в Приложении.
приведена в Приложении.
Для доказательства
сходимости полученной конечно-разностной
схемы я проверил условия теоремы,
приведенной в использованной мною
литературе, для матрицы А данной задачи.
Теорема утверждает, что если А –
самосопряженный и положительно
определённый оператор в пространстве
![]() сеточных функций и оператор
сеточных функций и оператор![]() (т.е. положительно определен в
(т.е. положительно определен в![]() ),
тогда стационарный двухслойный
итерационный процесс сходится в норме
),
тогда стационарный двухслойный
итерационный процесс сходится в норме![]() к точному решениюu системы
к точному решениюu системы![]() .
ГдеB=D+L, D - диагональ
матрицы А,L - элементы
матрицы А, расположенные ниже главной
диагонали. Для метода Зайделя
.
ГдеB=D+L, D - диагональ
матрицы А,L - элементы
матрицы А, расположенные ниже главной
диагонали. Для метода Зайделя![]() .
Текст программы pav_p.m,
реализующей эту проверку можно
найти в Приложении. В случае невыполнении
одного из условий теоремы, программа
выдаёт соответствующее сообщение об
ошибке, иначе сообщение о положительном
результате проверки. В данном случае
проверка матрицы А дала положительный
результат.
.
Текст программы pav_p.m,
реализующей эту проверку можно
найти в Приложении. В случае невыполнении
одного из условий теоремы, программа
выдаёт соответствующее сообщение об
ошибке, иначе сообщение о положительном
результате проверки. В данном случае
проверка матрицы А дала положительный
результат.
Также было получено несколько результирующихматриц u1, u2, u3, u4, которые здесь не были зафиксированы.
u1 приeps = 0.001;
u2 при eps = 0.0001;
u3 при eps = 0.00001;
u4 при eps = 0.000001;
Получили следующие нормы разности матриц:
NORM(u1-u2) =
0.0017
![]()
NORM(u2-u3) =
0.00012589
![]()
NORM(u3-u4) =
0.000016398
![]()
Приложение. Текст основной программы pavel.M.
% Ввод числа разбиений по X и по Y.
M = input('Input the grid size on X: ');
N = input('Input the grid size on Y: ');
h1 = 1/M;
h2 = 1/N;
q = h2/h1;
% Ввод погрешности вычислений.
eps = input('Input the quality (eps): ');
% Начальное заполнение искомой матрицы.
u = ones(M+1, N+1);
x = zeros(M+1,1);
y = zeros(N+1,1);
% Аппроксимация правой части
f = -1.*ones(size(u));
for i=1:M,
for j=1:N,
f(i,j)=30*(i/M*i/M+j/N*j/N-i/M-j/N);
end
end
% Аппроксимация граничных условий по X и заполнение служебного
% массива x(i).
for i = 1:(M+1),
u(i,1) = 0;
u(i,N+1) = sin(pi*(i-1)*h1/2);
x(i) = (i-1)*h1;
end
% Аппроксимация граничных условий по Y и заполнение служебного
% массива y(i).
for i = 1:(M+1),
u(i,1) = 0;
u(i,M+1) = 0;
x(i) = (i-1)*h1;
end
for j = 1:(N+1),
u(N+1,j) = 15*exp(pi)*sin(pi*(j-1)*h2);
u(1,j) = 15*sin(pi*(j-1)*h2);
y(j) = (j-1)*h2;
end
k = 0; % Инициализация числа выполненных шагов.
% Ввод параметра сходимости (рекомендуется mu = 1.536).
mu = input('Input the parameter mu ( 1<mu<2 ): ');
% Ввод максимального числа шагов.
MAX = input('Input the maximum number of steps MAX: ');
% Инициализация погрешности вычислений.
A = 100;
% Заблаговременное вычисление коэффициентов для ускорения
% рекуррентной процедуры.
a1 = 1/(2*(1+q^2));
a2 = q^2;
a3 = h2^2*a1;
% Условие продолжения цикла.
while (A > eps)
k = k + 1; % Инкремент числа шагов.
A = 0; % Инициализация погрешности.
for i=2:M,
for j=2:N,
% Собственно сами рекуррентные формулы.
X = a1 * (u(i,j-1) + u(i,j+1) + a2*u(i-1,j) + a2*u(i+1,j)) + a3*f(i,j);
X = mu*X + (1-mu)*u(i,j);
% Вычисление погрешности очередного шага
R = abs(X - u(i,j));
% и выбор наибольшей.
if (R > A) A = R; end
u(i,j) = X;
end
end
% Принудительный выход из цикла по ограничению на число шагов
% с выводом соответствующей диагностики.
if k == MAX
sprintf('%d Steps was made !!!', MAX)
break;
end
end
% Вывод результатов вычислений.
sprintf('Quality of approximation is %f', A)
if (k ~= MAX)
sprintf('Riched by %d steps', k)
end
mesh(x,y,u);
pause;
contour(x,y,u,50);
