Московский Государственный Институт Электронной Техники

(Технический Университет)

кафедра Высшей математики - I

КУРСОВАЯ РАБОТА

по

“Методам прикладной математики”

на тему

“Приближённое решение краевых задач математической физики методом сеток.”

Выполнил: студент

Гр. МП 35 Харитонов Р.Л.

Руководитель:

Москва 1999 г.

Методические указания и постановка задачи.

1. Тема.

Приближенное решение краевых задач математической физики методом сеток.

2. Цель работы.

Изучить основные понятия теории конечно-разностных методов решения краевых задач математической физики и уметь применять их на практике. Численное решение задачи осуществляется на персональной ЭВМ в среде MATLAB. Преимущество использования этой среды —богатый набор командных программ, реализующих большинство стандартных задач линейной алгебры и методов оптимизации, а также статистической обработки результатов. MATLAB обладает также хорошими графическими возможностями отображения результатов.

3. Порядок работы.

1. Познакомиться с основными понятиями метода сеток и методикой численного решения разностных уравнений, аппроксимирующих краевую задачу. Наиболее полно все основные понятия метода сеток изложены в [1,2]. Достаточной теоретической базой может служить методическое пособие [3].

2. Классифицировать уравнение и проверить корректность постановки данной в варианте краевой задачи и соответствие её физическому смыслу.

3. Разобраться с методикой построения неявных разностных схем конечно-разностных систем для данного типа уравнения.

4. Разобраться с устойчивыми методами решения явной и неявной схем.

5. Реализовать программу, осуществляющую решение в среде MATLAB.

6. Получить численные результаты для своего варианта. Оформить их в виде таблиц, построить необходимые кривые и поверхности уровней, иллюстрирующие решение задачи.

7. Оформить курсовую работу в соответствии с общим требованиями к курсовым работам. В теоретической части кратко осветить следующие вопросы:

• Классификация уравнения. Вскрыть физический смысл тех явлений, которые описываются данной математической постановкой задачи.

• Корректная постановка: граничные и начальные условия и их соответствие физическому смыслу.

• Понятия: сеточный шаблон, порядок аппроксимации разностных схем, сходимость, устойчивость решения.

• Выбор шагов сетки и оценка погрешности метода.

Порядок выполнения работы.

1. Классификация краевой задачи и её физический смысл

(*)

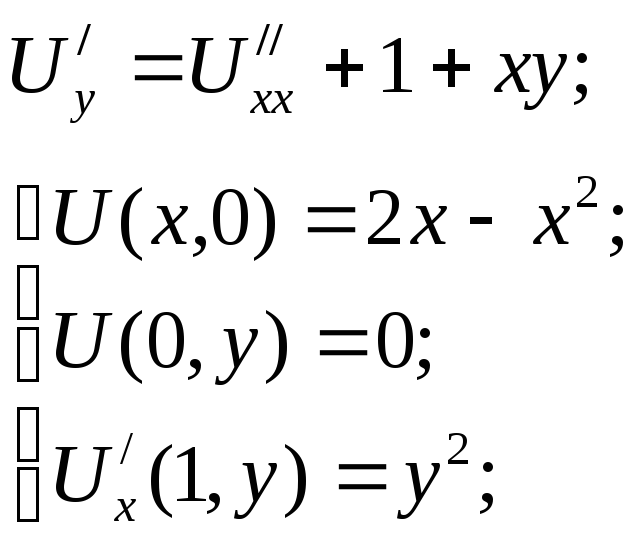
Линейное дифференциальное уравнение второго порядка такого вида относится куравнениям параболического типа. Данное уравнение описывает распределение тепла в однородном стержне длины 1 в зависимости от времени. Здесь переменная у имеет физический смысл времени, поэтому в дальнейшем будет рассматриваться такая задача:

(**)

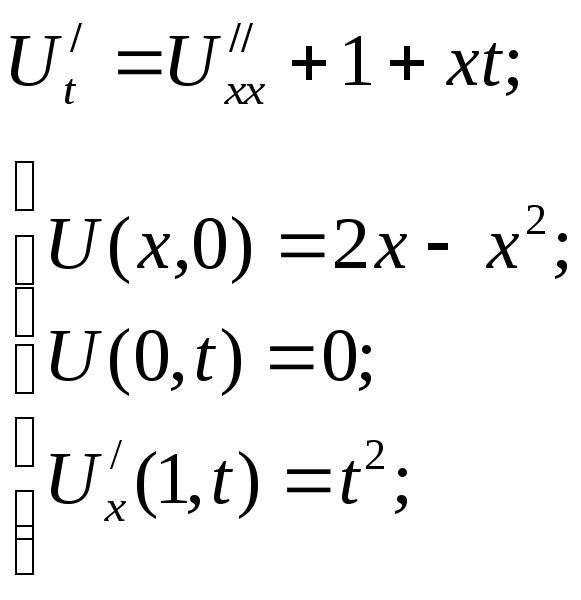гдеи ;

Так как общий вид уравнения теплопроводности имеет вид:

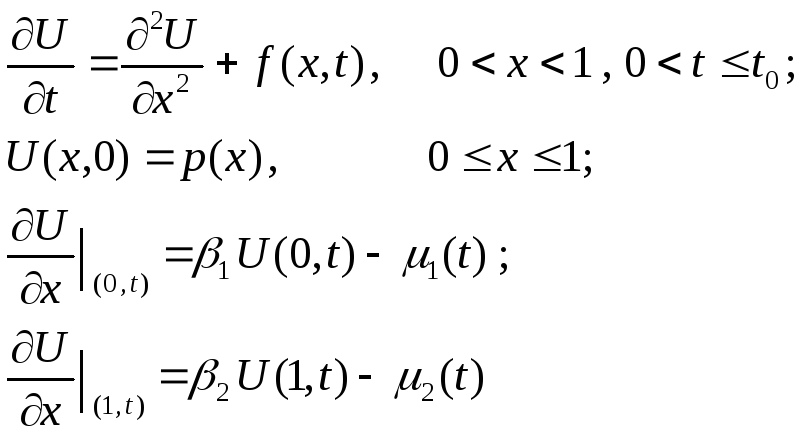
Для нашего случая можно записать:

(***)

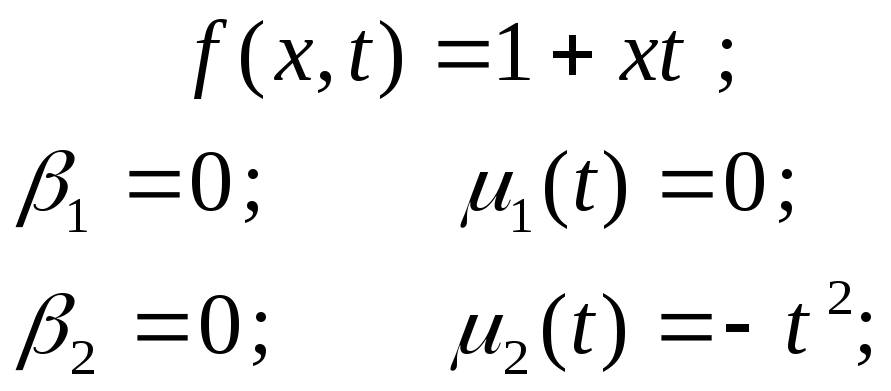В данной задаче начальные и граничные условия имеют следующий смысл.

Начальное условие задает распределение температуры на всём стержне в момент времени .

Граничное условие 3-го рода говорит о том, что на правом конце стержня по закону Ньютона происходит теплообмен с окружающей средой, температура которой в нашем случае зависит от времени и изменяется по указанному закону.

Граничное условие означает, что температура на левом конце стержня не зависит от времени.