IV. Метод сеток

Пусть - сетка в некоторой областиG; - линейное пространство сеточных функций, заданных на;- линейное пространство гладких функций;- норма в;- норма в. Предполагается, что

во-первых, существует оператор проектирования такой, что

для любого,

во-вторых, нормы исогласованы, т.е.

.

Рассмотрим некоторый дифференциальный оператор L, заданный в , и оператор, преобразующий сеточную функциюв сеточную функцию, заданную на.

Погрешностью аппроксимации оператора L разностным оператором называется сеточная функция:

,

в сеточном пространстве , гделюбая функция из.

Если при, то говорят, что разностный оператораппроксимирует дифференциальный операторL. Если при этом

то разностный оператор аппроксимирует дифференциальный операторL с порядком

Порядок выполнения работы

Классификация краевой задачи.

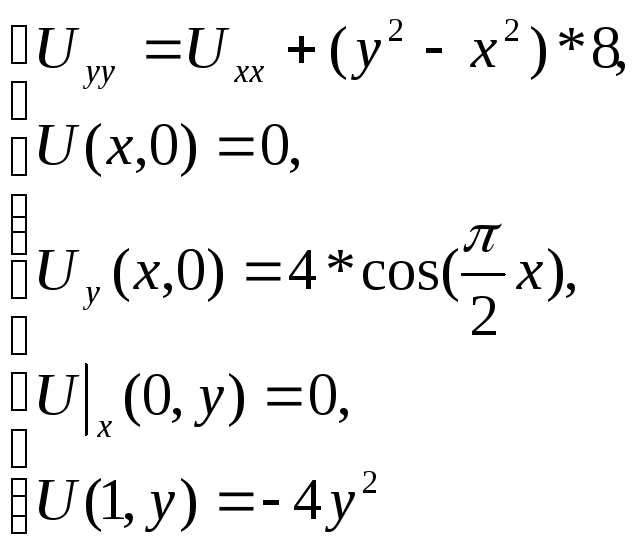
Линейное дифференциальное уравнение второго порядка такого вида относится к уравнениям гиперболического типа. Данное уравнение описывает колебание струны в зависимости от времени. Здесь переменная у имеет физический смысл времени, поэтому в дальнейшем будет рассматриваться такая задача:

гдеи.

Первая краевая задача для уравнения колебания струны состоит в поиске решения уравнения, удовлетворяющего начальному и граничным условиям.

В данной задаче начальные и граничные условия имеют следующий смысл:

Начальные условия (в начальный момент времени t=0):

задаёт форму струны.

задаёт распределение скоростей.

Граничные условия:

задает скорость на левом конце струны.

- закон движения правого конца струны.

Натяжение струны и плотность материала струны равны 1.

- плотность внешней силы, рассчитанная на единицу длины.

Явная разностная схема

j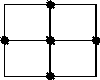+1 i i+1

j

j-1

Рис.1

Для сведения задачи к явной разностной схеме используем шаблон «крест», изображённый на рисунке 1.

Конечно-разностная схема для данной задачи имеет вид:

Обозначим и выразимчерез остальные значения сеточной функции, входящие в уравнение:

Для того чтобы система стала полностью определённой, дополним её уравнениями, полученными из аппроксимации краевых и начальных условий:

Для аппроксимации второго начального условия будем использовать конечно-разностную формулу второго порядка:

Вычтя из первого выражения второе получим формулу для начального условия второго рода с использованием мнимого узла.

Осталось аппроксимировать начальное условие второго рода на левом конце отрезка , имеющее следующий вид:

Для аппроксимации данного начального условия также будем использовать конечно-разностную формулу второго порядка с приведением ее к формуле с использованием мнимого узла:

.

Порядок аппроксимации данной разностной схемы равен .

Для нахождения решений используем уравнения.

Текст функции, вычисляющий матрицу решения размерностью MxN, приведены в Приложении.

Исследование на сходимость явной разностной схемы

При исследовании сходимости решения используем следующий метод: возьмём начальную сетку, вычислим значение Uв узлах этой сетки. Затем, увеличивая размерность матрицыU,при этом, оставляя первоначальные узлы, сравним максимальное расхождение двух матриц. Если эта величина будет монотонно убывать, то решение сходится и схема устойчива.

Результаты исследования сходимости матрицы решения следующие:

Размерность U : 100x110 ; 200x210;300x310.

Таблица норм (максимальных расхождений)

Размерность U	1100х110	200х220	200х210		400х420
Норма (U2-U1)	3,6734*10-4		9,9334*10-5
Размерность U	1300х310	600х620
Норма (U2-U1)	4,5368*10-5

То есть решение сходится, если выполнено условие: .

Таблица решения

x\t	0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
0	0 0.3984 0.7869 1.1561 1.4968 1.8006 2.0602 2.2690 2.4219 2.5152 2.5465
0,1	0 0.3931 0.7756 1.1383 1.4720 1.7685 2.0204 2.2214 2.3665 2.4518 2.4752
0,2	0 0.3773 0.7420 1.0851 1.3979 1.6725 1.9017 2.0795 2.2009 2.2625 2.2619
0,3	0 0.3513 0.6867 0.9977 1.2761 1.5144 1.7060 1.8453 1.9275 1.9494 1.9090
0,4	0 0.3159 0.6110 0.8777 1.1085 1.2968 1.4363 1.5220 1.5497 1.5164 1.4202
0,5	0 0.2717 0.5164 0.7275 0.8984 1.0233 1.0968 1.1144 1.0725 0.9685 0.8006
0,6	0 0.2198 0.4049 0.5499 0.6494 0.6984 0.6925 0.6281 0.5019 0.3120 0.0568
0,7	0 0.1613 0.2789 0.3485 0.3659 0.3275 0.2297 0.0697 -0.1549 -0.4457 -0.8039
0,8	0 0.0975 0.1408 0.1269 0.0529 -0.0836 -0.2850 -0.5533 -0.8900 -1.2964 -1.7731
0,9	0 0.0299 -0.0065 -0.1107 -0.2842 -0.5283 -0.8441 -1.2327 -1.6947 -2.2309 -2.8416
1	0 -0.0400 -0.1600 -0.3600 -0.6400 -1.0000 -1.4400 -1.9600 -2.5600 -3.2400 -4.0000

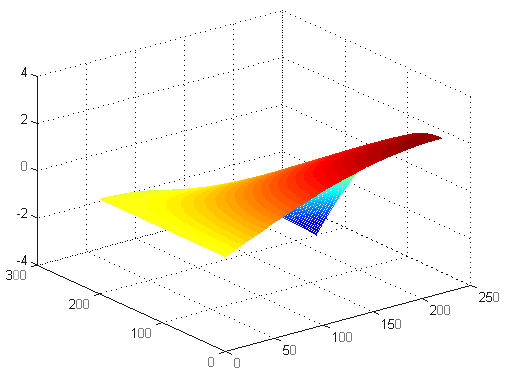
Форма струны в разные моменты времени.

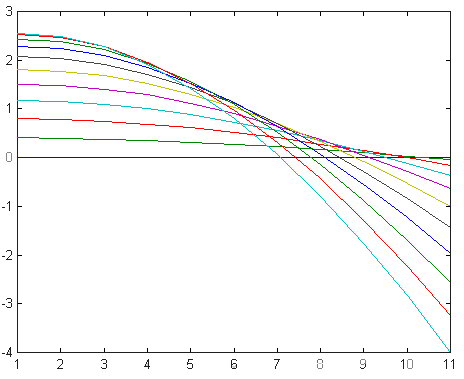
График, иллюстрирующий решение

Неявная разностная схема

Для аппроксимации используем Т-образный пятиточечный шаблон:

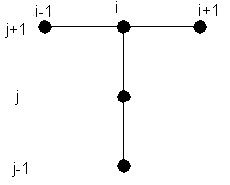
(1)

Уравнение аппроксимируется следующей системой разностных уравнений:

с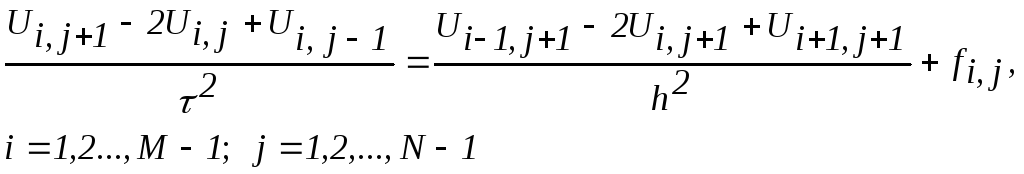погрешностью аппроксимации.

Начальные условия аппроксимируем с порядком аналогично тому, как это делалось для явной схемы.

.Обозначим и запишем (1) следующим образом:

Краевые условия аппроксимируем также как и в явной схеме.

Неявная разностная схема аппроксимирует краевую задачу с погрешностью.

Вычисления прогоночных коэффициентов.

Прогонка осуществляется послойно, т. е. при каждом фиксированном j, начиная с j=2(при j=0 “работают” начальные условия).

Запишем системы, необходимые для решения задачи методом прогонки, с использованием аппроксимированных начальных и краевых условий.

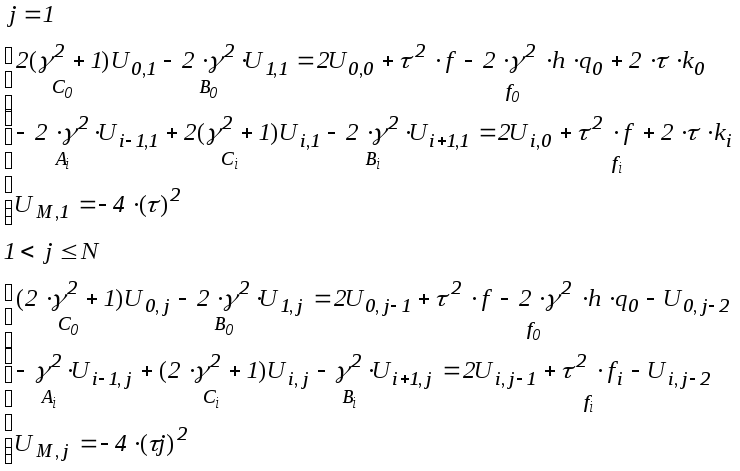
При прогонке различают прямой и обратный ход:

при прямом ходе определяются коэффициенты инаj-ом

слое:

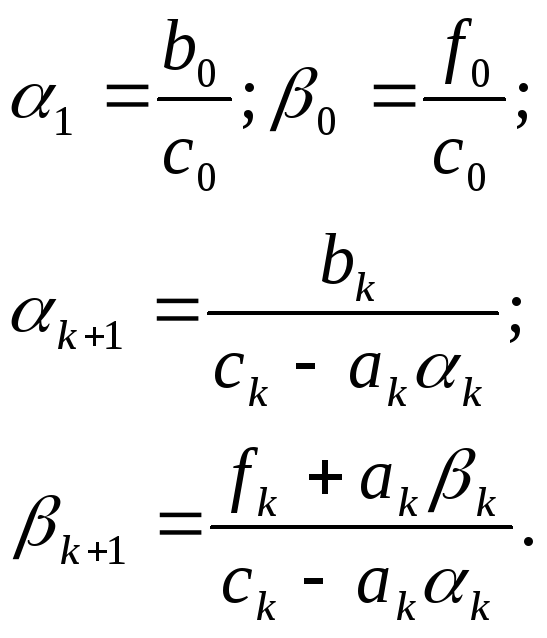
при обратном ходе вычисляются значения функции на j-ом слое:

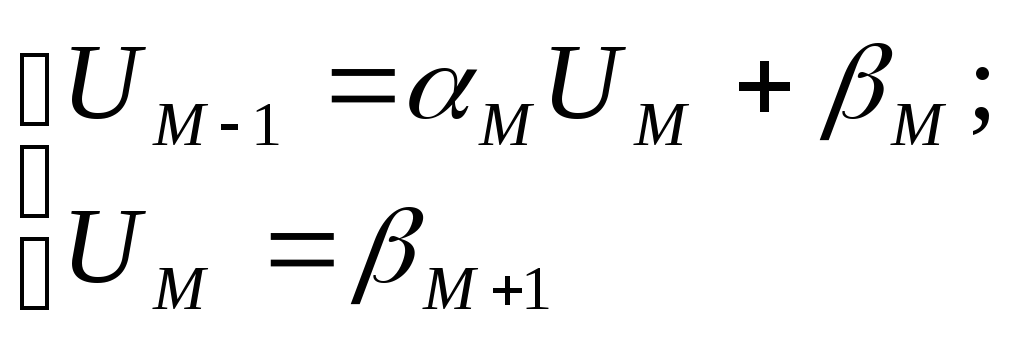
Используя метод прогонки, получаем решение неявной разностной схемы для данной задачи.

Текст функции, вычисляющий матрицу решения размерностью MxN, приведен в ПРИЛОЖЕНИИ.

При исследовании сходимости решения используем следующий метод: возьмём начальную сетку, вычислим значение Uв узлах этой сетки. Затем, увеличивая размерность матрицыU,при этом, оставляя первоначальные узлы, сравним максимальное расхождение двух матриц. Если эта величина будет монотонно убывать, то решение сходится и схема устойчива.

Результаты исследования сходимости матрицы решения следующие :

Размерность U : 100x110;200x210 ;300x310.

Таблица норм (максимальных расхождений)

Размерность U	100х110	200х220	200х210	400х420	300х310	600х620
Норма (U2-U1)	0.0283387		0.0150138		0.0102089

То есть решение сходится, если выполнено условие: .

2.2.2. Таблица решения.

x\t	0 0,1 0,2 0,3 0,4 0,5 0,6	0,7 0,8 0,9 1
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1	0 0.4000 0.7898 1.1597 1.5009 1.8049 2.0643 0 0.3947 0.7785 1.1419 1.4761 1.7727 2.0246 0 0.3789 0.7449 1.0888 1.4022 1.6770 1.9062 0 0.3530 0.6897 1.0016 1.2805 1.5192 1.7109 0 0.3176 0.6141 0.8818 1.1133 1.3020 1.4414 0 0.2734 0.5196 0.7318 0.9035 1.0287 1.1011 0 0.2215 0.4082 0.5544 0.6546 0.7029 0.6959 0 0.1631 0.2822 0.3530 0.3701 0.3308 0.2321 0 0.0993 0.1441 0.1300 0.0557 -0.0814 -0.2834 0 0.0316 -0.0047 -0.1092 -0.2829 -0.5272 -0.8433 0 -0.0400 -0.1600 -0.3600 -0.6400 -1.0000 -1.4400	2.2729 2.4257 2.5189 2.5496 2.2255 2.3704 2.4553 2.4775 2.0839 2.2049 2.2650 2.2629 1.8498 1.9307 1.9509 1.9090 1.5259 1.5520 1.5171 1.4195 1.1173 1.0740 0.9686 0.7996 0.6302 0.5029 0.3118 0.0556 0.0712 -0.1544 -0.4461 -0.8050 -0.5523 -0.8897 -1.2967 -1.7739 -1.2322 -1.6946 -2.2311 -2.8421 -1.9600 -2.5600 -3.2400 -4.0000

Форма струны в разные моменты времени.

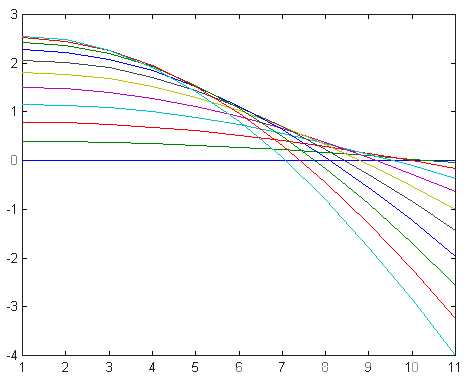
График, иллюстрирующий решение.