Решение задачи с помощью неявной разностной схемы

В неявной схеме для получения решения на последующем слое необходимо решать систему алгебраических уравнений специального вида. Преимущество использования неявных схем заключается в существенном ослаблении требований к шагам сетки для выполнения условия устойчивости.

Рассмотрим снова нашу краевую задачу. Для аппроксимации уравнения используем следующий шаблон:

(i-1 , j+1)

(i , j+1)

(i-1 ,j+1)

( i , j)

Аппроксимация дифференциального уравнения

(4)

Приведем (4) к виду, удобному для применения метода прогонки:

(5)

Аппроксимация начального условия

(6)

Аппроксимация 3-го граничного условия

Граничное условие второго рода выглядит следующим образом:. Для его аппроксимирования разложим U(x,y) в окрестности точки (1,у) в ряд Тейлора:

Используя исходное уравнение и граничное условие, получим:

Перейдем к конечным разностям, записываемым в узле (М-1,j), т.е. на предпоследнем слое:

отсюда

(8)

Таким образом, построена неявная разностная схема аппроксимирующая краевую задачу с погрешностью аппроксимации порядка . Полученная система линейных алгебраических уравнений (5)-(8) описывается трехдиагональной матрицей:

и в общем случае имеет вид:

где (9)

Для решения таких систем применяется метод прогонки.

Вычисления прогоночных коэффициентов

Из (7) имеем:

Из (8) получаем:

На основе (5) можно записать:

Алгоритм решения системы (9) состоит из двух этапов: прямого и обратного хода прогонки. Обозначим , тогда из первого уравнения системы следует:

Подставим во второе уравнение системы (9) приi=1 и выразим :

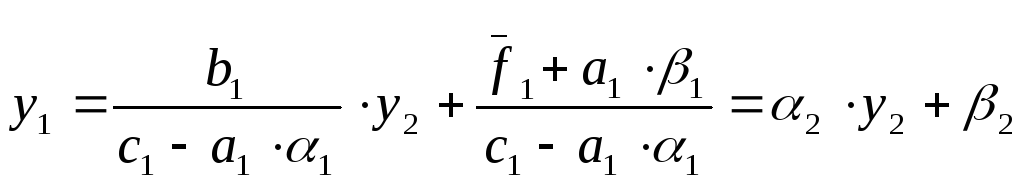
Продолжая подстановку далее, получим на к-ом шаге уравнение

, к =1,2,…М-1 (10)

где и; (11)

причём (12)

Формулы (11) определяют прямой ход прогонки, в результате которого рекуррентно вычисляются прогоночные коэффициенты и. Далее по известному коэффициентуиз (12) определяютсяи, а затем по формуле (10) находятся остальные. Это обратный ход прогонки.

Устойчивость и корректность метода прогонки обеспечивается при условии выполнения следующей теоремы:

если коэффициенты системы уравнений метода прогонки удовлетворяют следующие условия

причем хотя бы одно из неравенств {1} или {2} является строгим, тогда для метода прогонки имеют место неравенства:

которые гарантируют корректность и устойчивость метода прогонки. Выполнение этих условий проверяется в процессе работы программы.

Решим, модельную задачу, основываясь на выводах, сделанных ранее.

Пусть есть функция U(x,y)=exp(-3t-x+1).

Тогда наша задача будет выглядеть следующим образом.

При помощи алгоритмов, выведенных ранее, получим решение:

Для явной схемы:

oshibka_yav =

0.03431069753037

otn =

6.284223459868889e-004

Для неявной схемы:

oshibka_neyav =

0.0240

otn =

4.3881e-004

Отсюда можно сделать вывод, о верности, выведенного алгоритма нахождения решения дифференциального уравнения.

Приложение 1.

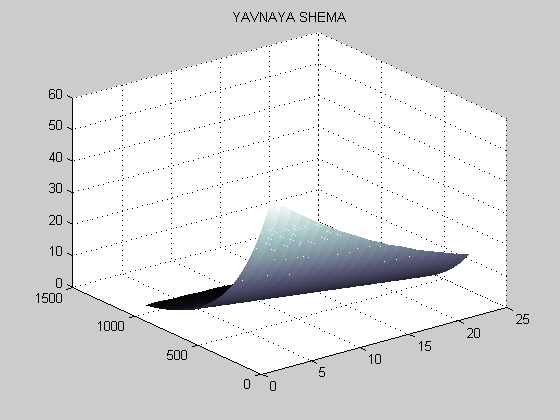
Поверхности.

Явная схема.

Точное решение

Неявная схема.

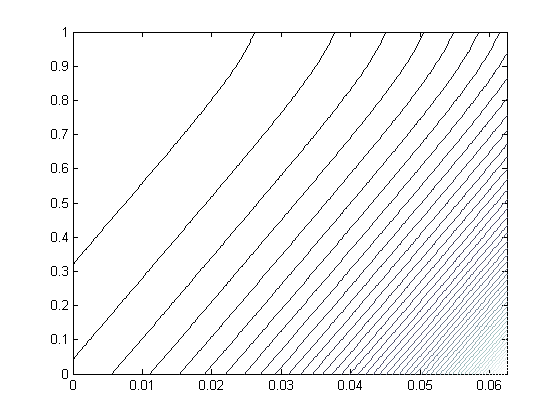
Изолинии.

Явная схема.

Неявная схема.

Зависимость от при фиксированных .

Явная схема.

Неявная схема.

Посмотрим на изменение ошибки при изменении числа узлов в два раза.

Для явной схемы будем увеличивать количество узлов лишь по t, так как порядок аппроксимации схемы O(t+h^2) и изменение по h не внесет существенного вклада

Для явной схемы

N*N	20*800-20*1600	20*1600-20*3200	20*3200-20*6400	20*12800-20*6400
U1-U2	0.0037429775308	0.0018732432856	9.370606841715794e-004	4.686401538828076e-004

Для неявной схемы

N*N	50*50-100*100	200*200-100*100	400*400-200*200	800*800-400*400
U1-U2	0.0618365465453	0.02955446645149	0.01511306461572	0.00752819544453

Как и следовало ожидать, ошибка уменьшается в два раза.

При сравнении явной и неявной схемы на сетке 20*800

Получим следующие результаты:

Максимальная абсолютная ошибка = 8.81445002437874

Максимальная относительная ошибка =0.00161442283649

На сетке 20*1600

Максимальная абсолютная ошибка = 0.36487191683818

Максимальная относительная ошибка =6.682862269448353e-005