§3 Разностная аппроксимация дифференциальных операторов.

Пусть дан линейный дифференциальный оператор L, действующий на функцию v=v(x). Заменяя входящие в Lv производные разностными отношениями, получим вместо Lv разностное выражение L_hv_h, являющееся линейными комбинациями значений сеточной функции v_h на некотором множестве узлов сетки, называемом шаблоном. Такая приближенная замена Lv на L_hv_h называется аппроксимацией дифференциального оператора разностным оператором ( или разностной аппроксимацией оператора L).

Изучение разностных аппроксимаций оператора L вначале производят локально, т.е. в любой фиксированной точке x области _h. Прежде чем приступать к разностной аппроксимации оператора необходимо выбрать шаблон, т.е. указать множество соседних с узлом х_i узлов, в которых значения сеточной функции v_h(x_i)=v(x_i) могут быть использованы для аппроксимации оператора L. Подробнее об этом будет рассказано в разделе “Решение задачи”.

Решение задачи.

Задание: получить приблизительное решение данной краевой задачи уравнения в частных производных математической физики методом сеток. (1)

(2)

Приведем задачу к стандартному виду, заменой вида x’=x\L, t’=a^2t\L, тогда уравнение примет вид:

В дальнейшем, будем опускать штрихи.

Классификация задачи.

Данное уравнение является уравнением параболического типа и физически отражает процесс распределения тепла в однородном стержне длины 1.

Искомое решение - значение температуры стержня в точкеx в момент времени y.

Данная краевая задача состоит в нахождении функции, удовлетворяющей уравнению (1), а также заданным начальным и граничным условиям (2)

, - граничное условие первого рода, означающее, что температура на левом конце стержня изменяется со временем по заданному закону

- граничное условие третьего рода, означачающее, что поток тепла на правом конце стержня по закону Ньютона происходит теплообмен с окружающей средой

Функция имеет смысл плотности источников тепла.

Решение задачи с помощью явной разностной схемы

В явной разностной схеме значение сеточной функции на последующем слое полностью определяется значением её на предыдущем слое по рекуррентным формулам.

Аппроксимация дифференциального уравнения

Для сведения задачи к явной разностной схеме используем следующий шаблон:

Получаем конечно-разностную систему:

(3)

Выразим через остальные значения сеточной функции, входящие в уравнение:

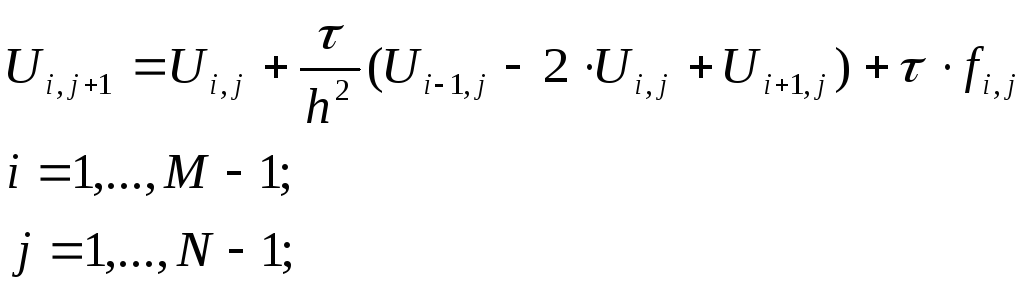(3*)

Уравнение (3*) должно выполняться для всех внутренних узлов сетки. Для того чтобы система стала полностью определенной, необходимо дополнить ее уравнениями, получаемыми из аппроксимации краевых и начальных условий.

Аппроксимация начального условия.

Аппроксимация 3-го граничного условия.

Граничное условие третьего рода выглядит следующим образом: Для его аппроксимирования разложим U(x,y) в окрестности точки (L,у) в ряд Тейлора:

Используя исходное уравнение и граничное условие, получим:

Перейдем к конечным разностям, записываемым в узле (L,j), т.е. на первом слое:

отсюда

Порядок аппроксимации данной разностной схемы

Устойчивость решения.

Несмотря на очевидную простоту данной вычислительной процедуры, её практическая реализация возможна лишь при таких соотношениях между шагами сетки иh, при которых выполняется условие устойчивости решения к ошибкам и неточностям в начальных данных. Для параболического уравнения это условие имеет вид: . Если условие устойчивости разностной схемы не будет выполнено, то в процессе рекуррентного решения возможно накапливание ошибок от слоя к слою, что приведёт к неудовлетворительному результату, несмотря на высокую точность аппроксимации дифференциальной краевой задачи разностной схемой.