2.8. Полином Лагранжа

Для построения интерполяционного многочлена прямым методом необходимо предварительно решить систему линейных уравнений (2.16). Интерполяционная формула Лагранжа не требует решения системы уравнений (2.16). В общем виде полином Лагранжа можно представить формулой:

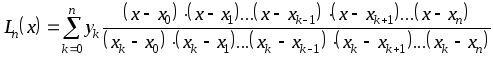(2.17)

где - узлы интерполяционной сетки, - значения функциив узловых точках.

Каждый из слагаемых формулы (2.17), как нетрудно убедиться, является полиномом степени n, следовательно - также есть полиномn-ой степени (как сумма многочленов n-ой степени). Структура формулы (2.17) построена таким образом, чтобы выполнялось условие , в чем нетрудно убедиться.

Если функция достаточно гладкая, т.е. имеет непрерывные производныевплоть до(n+1)- порядка включительно, то погрешность интерполяции (остаточный член), определяемую формулой

,

можно оценить следующим образом:

, (2.18)

где

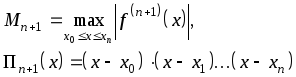
Полином Лагранжа полезен тем, что в явном виде содержит значение функции .

2.9. Интерполяционная формула Ньютона

Рассмотрим регулярную интерполяционную сетку с равноотстоящими узлами: , где h- шаг интерполяции, .

Интерполяционную формулу будем искать в виде:

(2.19)

Предварительно составим таблицу конечных разностей функции (таблица 2.1). В таблице приняты следующие обозначения:

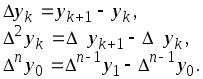
Можно показать, что для того, чтобы выполнялись условия интерполяции, необходимо и достаточно, чтобы

(2.20)

или

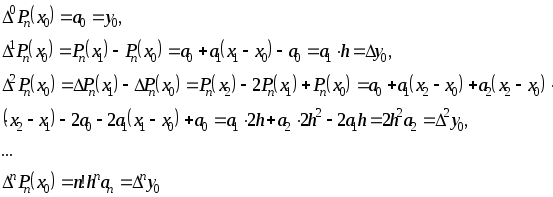
откуда нетрудно получить формулы для вычисления коэффициентов :

(2.21)

Подставив (2.21) в (2.19) получим

(2.22)

Выражение (2.22) является первой интерполяционной формулой Ньютона. Погрешность интерполяции для формулы Ньютона можно вычислить следующим образом.

Предположим, что функция (n+1) раз дифференцируема. Введем переменную , тогда ошибка метода может быть вычислена по формуле:

, (2.23)

где . Если известна конечная разность , то погрешность интерполяционной формулы можно оценить приближенно по формуле:

.

Интерполяционная формула Ньютона представляет собой просто другой способ составления интерполяционного многочлена. Она полезна, поскольку число используемых узлов может быть легко увеличено или уменьшено без перевычисления остальных коэффициентов полинома в форме Ньютона. Интерполяционная формула Ньютона используется только для регулярных сеток.

2.10. Интерполяционные сплайн-функции

Использование интерполяционных многочленов при восполнении дискретно заданных функций с конечной и невысокой гладкостью имеет свои недостатки.

1. При большом количестве узлов интерполяции наблюдается осцилляция многочлена между узловыми точками.

2. Большое количество арифметических операций, свойственное многочленам высоких степеней, с одной стороны увеличивает величину погрешностей результатов вычислений на ЭВМ (за счет накопления ошибок округления), с другой - приводит к значительным затратам машинного времени.

Можно избежать практически всех перечисленных выше недостатков, если в качестве интерполянта использовать сплайн-функции.

Определение. Интерполяционным сплайном называют функцию, гладко склеенную из кусков функций некоторого класса и проходящую через узлы интерполяции.

Если в качестве носителя сплайн-функции используется полиномы, то сплайн называется полиномиальным. На практике обычно применяют полиномиальные сплайн-функции. Пусть задана интерполяционная сетка

(2.23)

Функцию будем называть полиномиальным сплайном, если

а) ,

б) - принадлежит классу непрерывных функций на [a,b] вместе со своими производными, вплоть доn-1 порядка;

с) .