16

Кафедра ткс, Цифровая обработка сигналов Лабораторная работа 1.

Преобразование Фурье. Спектральный анализ сигналов.

Цель работы.

Целью работы является получение навыков работы с преобразованием Фурье. Умение находить АЧХ и ФЧХ сигналов. Изучение свойств этих характеристик. Умение применять дискретное преобразование Фурье (ДПФ) для нахождения спектра сигналов в среде MATLAB.

Теоретические сведения. Преобразование Фурье.

Кроме временного представлениясигналов, где сигнал это функция времениs(t), при анализе и обработке сигналов, используется такжечастотное представлениесигнала в виде функции частотыS( f ) . Функцииs( t ) иS( f ) связаны друг с другомпреобразованием Фурье.

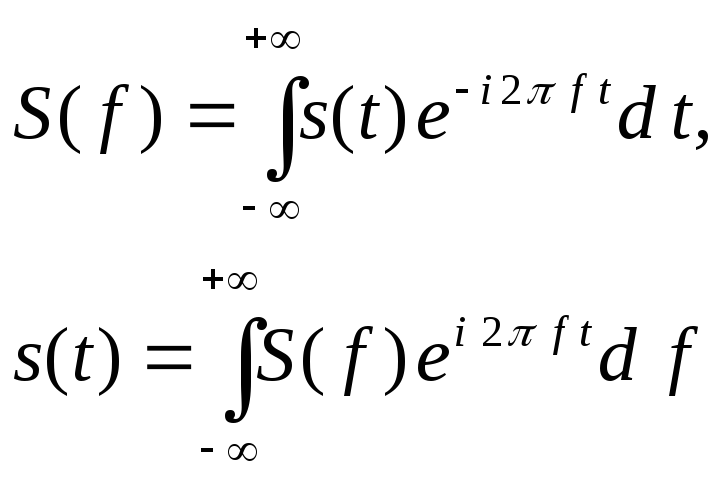(1)

Здесь первое выражение называется прямое преобразование Фурье, а второе выражение называетсяобратное преобразование Фурье. ФункцияS( f ) называетсяспектром сигналаs( t ).

Функция S( f ) является комплексной функцией, и может быть представлена в алгебраической и показательной форме.

Из спектра S( f ) можно получитьамплитудно-частотную характеристику(АЧХ)A( f ) ифазово-частотную характеристику(ФЧХ)( f ) сигнала, с помощью соотношений.

(2)

Отметим некоторые из свойств, преобразования Фурье. Первое, если сигнал вещественная функция, то для спектраS( f ) выполняются следующие соотношения четности

Здесь звездочка означает комплексное сопряжение. Из этих соотношений видно, что для вещественного сигнала, АЧХ - четная функция, а ФЧХ – нечетная функция.

Второе, если сигнал вещественная четная функция времени

,

то для спектра выполняются следующие соотношения

Здесь мнимая часть спектра равна нулю.

Третье, если сигнал вещественная нечетная функция времени

,

то для спектра выполняются следующие соотношения

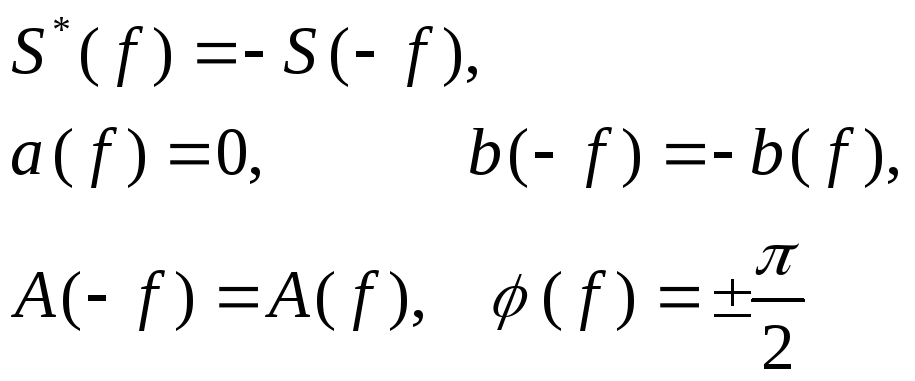
Здесь действительная часть спектра равна нулю.

В качестве первого примерарассмотрим прямоугольный импульс, центрированный относительно начала отсчета времени и имеющий длительность.

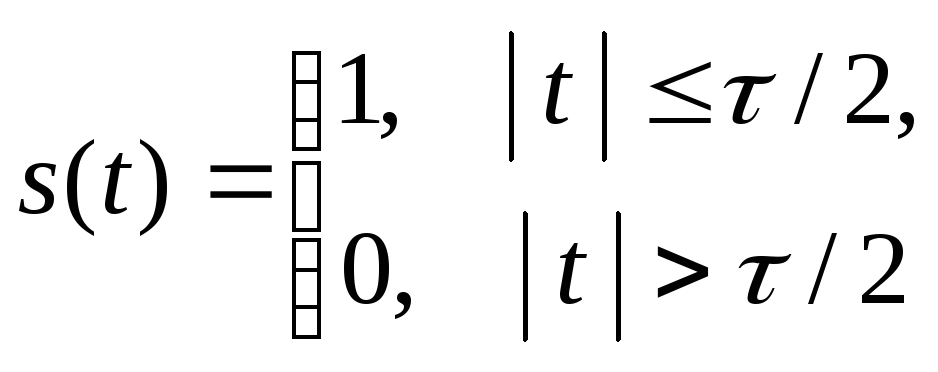
Вычисляем спектр S(  ) с помощью прямого преобразования Фурье

Здесь использована циклическая частота  = 2  f. При нахождении АЧХ и ФЧХ надо учесть, что рассматриваемый прямоугольный импульс является действительной четной функцией времени. Следующие рисунки показывают импульс и его АЧХ и ФЧХ.

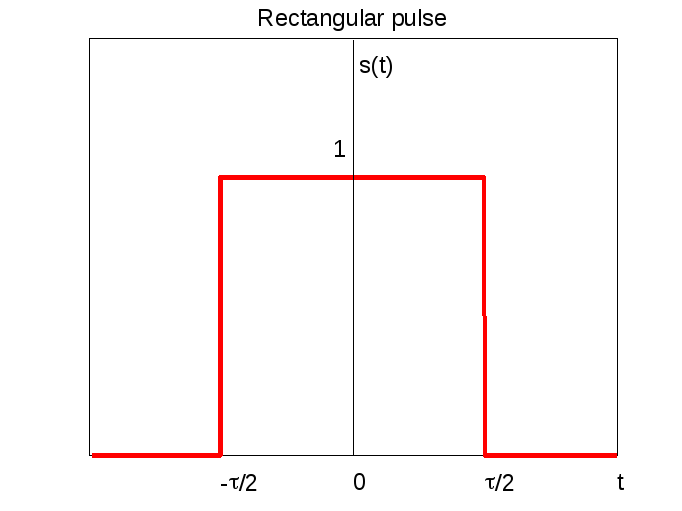
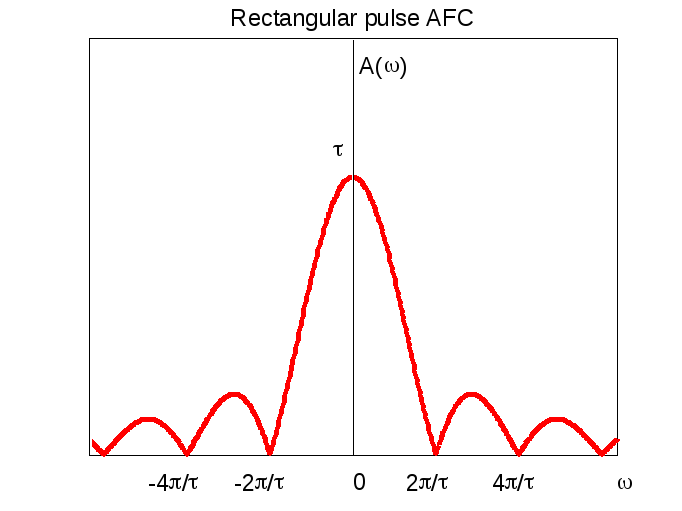
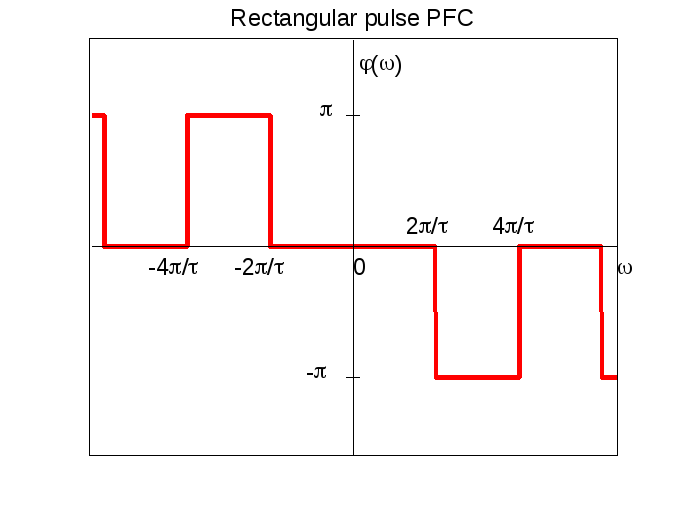
Обратим внимание на то, что сигнал действительная четная функция. Поэтому АЧХ четная функция, ФЧХ нечетная функция.

Спектр данного сигнала (АЧХ) простирается до бесконечности, постепенно затухая. Поэтому вводят понятие эффективной ширины спектра. Как видно из графиков, спектр имеет лепестковый характер и ширина главного лепестка равна

При лепестковом характере спектра за эффективную ширину спектра принимают ширину главного лепестка. Длительность прямоугольного импульса равна

Произведение эффективной ширины спектра сигнала на длительность сигнала называется базой сигнала(processinggain).

Для каждого сигнала это свое число. В случае прямоугольного импульса это есть

Из этих соотношений видно, что чем короче сигнал, темшире его спектри наоборот. Это положение называютсоотношением неопределенности. Существует утверждение, что для любого сигнала база сигнала не может быть меньше единицы.

В литературе, посвященной теории сигналов, встречается определение базы сигнала отличающееся от приведенного определения на 2 . В этом определении эффективная ширина спектра  , измеряемая врад/с, заменяется на ширину спектра f, измеряемую в герцах.

Второй пример. Рассмотрим односторонний экспоненциальный импульс

где a > 0 произвольное положительное число.

Вычисляем спектр S(  ) с помощью прямого преобразования Фурье

Следующие рисунки показывают экспоненциальный импульс и его АЧХ и ФЧХ

Для экспоненциальных сигналов в качестве длительности сигнала обычно берется время, при котором амплитуда сигнала убывает e = 2.7…раз. Поэтому длительность экспоненциального сигнала равна

Будем определять эффективную ширину спектра по уровню 0.1 от максимума. Из графика видно, что эта ширина составляет примерно

Таким образом, база экспоненциального сигнала равна

Третий пример. Рассмотрим спектр периодического сигнала. Пусть это будет гармонический сигнал с частотойf₁.

Используя формулу Эйлера просто получить спектр этого сигнала.

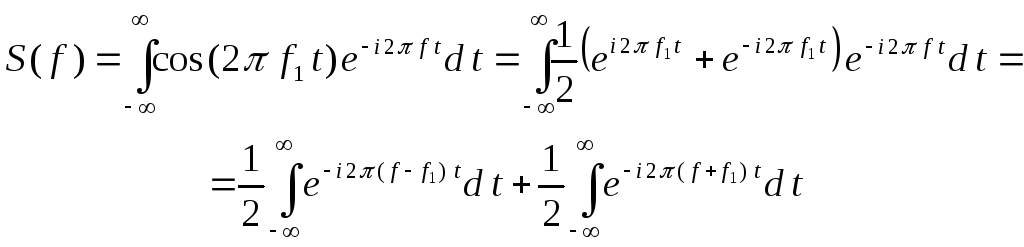
Далее используем интегральное представление дельта-функции.

Поэтому спектр сигнала есть суперпозиция дельта-функций.

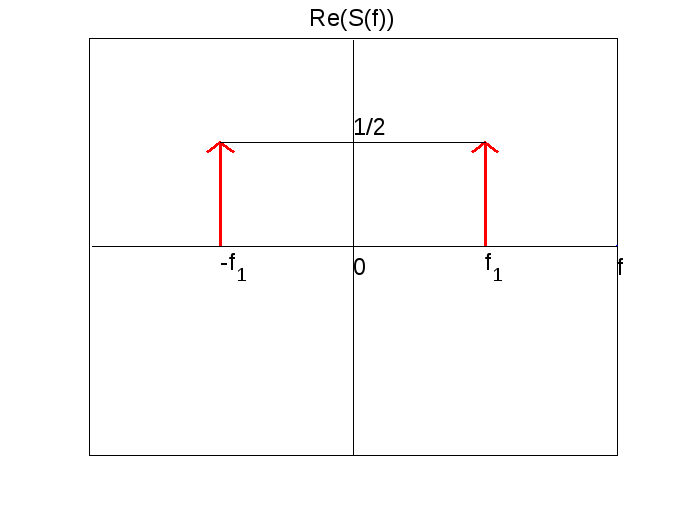
Рассматриваемый сигнал есть действительная четная функция, поэтому по всем правилам мнимая часть спектра равна нулю, действительная часть показана на рисунке.

Возьмем в качестве гармонического сигнала нечетную функцию.

В этом случае получаем следующий спектр сигнала.

Рассматриваемый сигнал есть действительная нечетная функция, поэтому действительная часть спектра равна нулю, мнимая часть спектра показана на рисунке

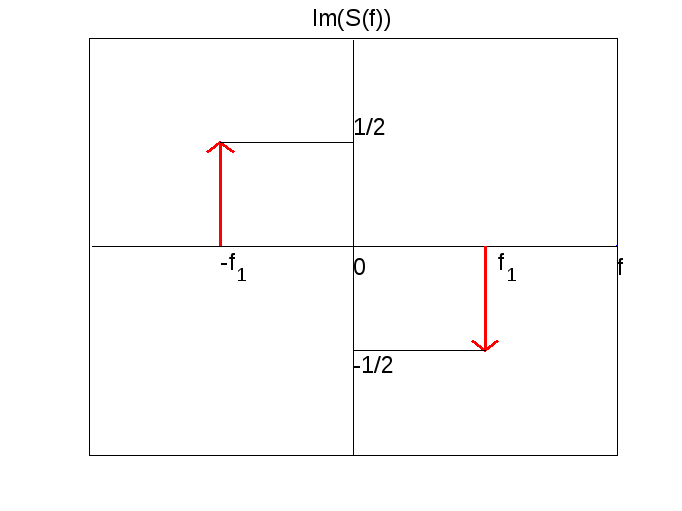
Если рассматривать произвольный периодический сигнал, то, как известно, его можно разложить в ряд Фурье. Поэтому любой периодический сигнал есть суперпозиция синусов и косинусов с разными частотами. Поэтому спектр любого периодического сигнала есть сумма дельта-функций с разными частотами и разными амплитудами. График спектра в этом случае представляет собой набор стрелок разной длины и направленных вверх или вниз. Такой спектр называют линейчатым спектром. Рассмотренные ранее спектры называютсплошным спектром. Для линейчатого спектра не имеет смысл ФЧХ как функция частоты( f ). АЧХ периодических сигналов имеет линейчатую структуру.

Теоретические сведения. Дискретное преобразование Фурье.

Если преобразование Фурье сводится к аналитическим выражениям, то задача нахождения спектра сигнала решается просто. Чаще всего этого сделать невозможно, поэтому приходится вычислять интеграл Фурье численными методами. Рассмотрим финитный сигнал s( t ). Выберем временной интервалt  [ -T/2, T/2 ] такой, чтобы вне этого интервала сигнал равнялся нулюs( t ) = 0.

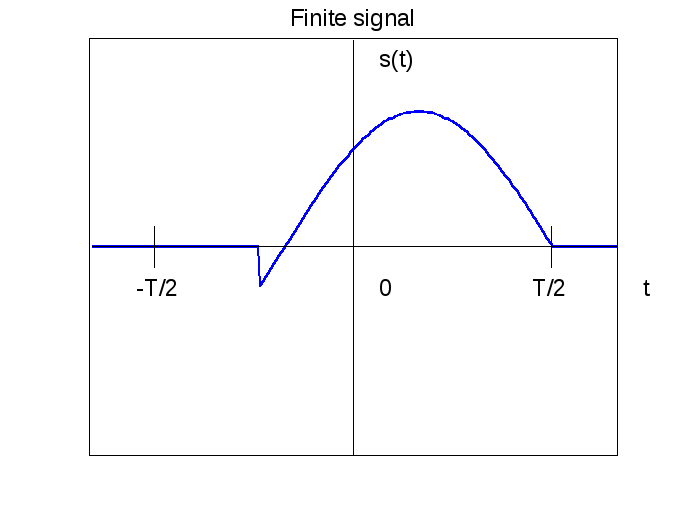
Тогда спектр S( f ) такого сигнала будет равен интегралу с конечными пределами.

(3)

Этот интеграл можно вычислить разными численными методами с большей или меньшей точностью. Мы выберем метод прямоугольников. Проведем дискретизацию сигнала с шагом дискретизации

где Nчетное число. Отсчеты сигналаs_n = s( t_n ) берем в дискретные моменты времени

В методе прямоугольников интеграл (3) заменяем следующей суммой

(4)

Мы собираемся вычислять эту сумму, используя дискретное преобразование Фурье (ДПФ) из пакета MATLAB. Прямое и обратное преобразование ДПФ задаются следующими суммами

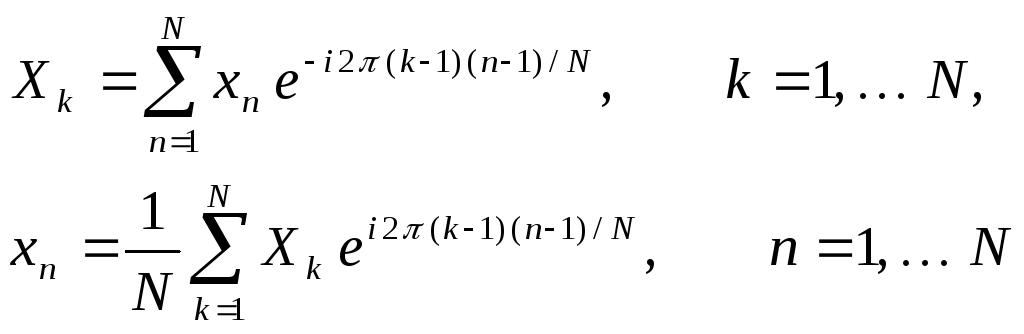(5)

Чтобы сумма (4) приняла вид прямого преобразования ДПФ, надо перейти к дискретному набору частот по формуле

Здесь интервал дискретизации  fна оси частот определяется соотношением

т.е. интервал  fобратно пропорционален интервалу интегрированияT. Спектр сигнала теперь определяется только при дискретных значениях частот

Формула спектра (4) для дискретных значений частоты f_mпринимает вид.

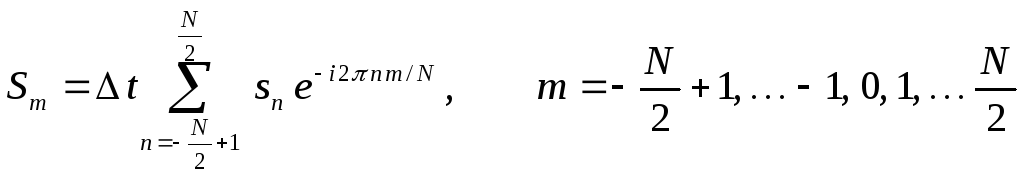(6)

Частотный спектр по формуле (6) определяется только в интервале частот

Здесь максимальное значение частоты равно

Как известно, выражение в правой части это равенства есть частота Найквиста (Nyquist).

Таким образом, максимальная частота равна частоте Найквиста. Поэтому Формула (6) позволяет описывать спектр таких сигналов, у которых частоты не превышают частоту Найквиста.

Формулы (6) для спектра S( f ) и (5) для прямого преобразования ДПФ похожи друг на друга, но не совпадают полностью. Отличие этих формул в интервалах изменения индексов. Поэтому прежде чем использовать ДПФ для нахождения спектра нужно проделать некоторые преобразования. Эти преобразования рассмотрим по пунктам.

1) Умножим уравнение (6) на экспоненту

В результате получим выражение

(7)

2) В сумме (7) сделаем замену индексов

В результате получим следующее выражение

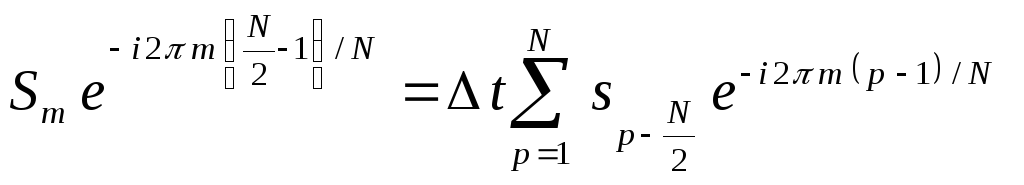(7)

3) Обозначим отсчеты сигнала через последовательностьx_nв преобразовании ДПФ (5) по формуле.

В результате получим выражение

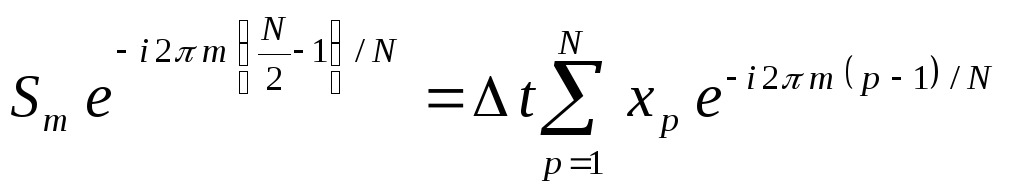(8)

4) Индекс mменяется в интервале

(9)

Разобьем этот интервал на две части. Рассмотрим сначала правую часть этого интервала

Сделаем замену индексов в уравнении (8).

В результате получим следующее выражение

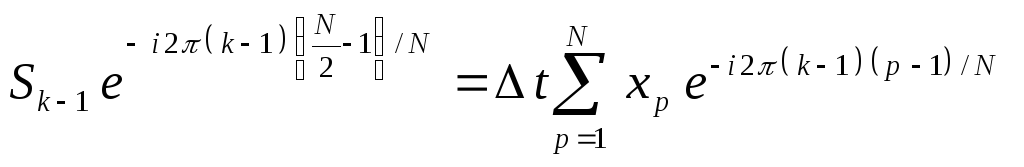(10)

Теперь сумма в уравнении (10) полностью совпадает с X_kпрямым дискретным преобразование Фурье (5). Таким образом, мы получаем формул для вычисления половины спектра

(11)

5) Теперь рассмотрим левую часть интервала (9)

Сделаем теперь другую замену индексов в уравнении (8).

В результате получим выражение

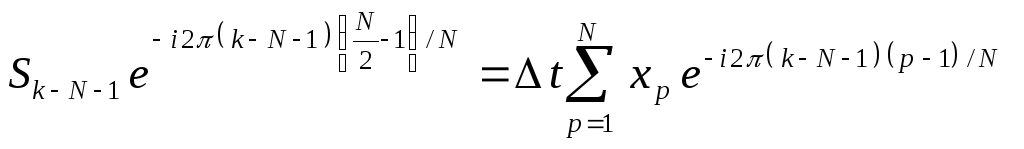(12)

В уравнении (12) преобразуем экспоненты. Так как Nчетное число, то

целое число. Целым число является также p – 1. Поэтому все экспоненты имеют одинаковый вид

(13)

где Mцелое число. Преобразуем экспоненту (13).

Здесь одна из экспонент равна единице по формуле Эйлера

После этих преобразований, уравнение (12) принимает вид

(14)

Теперь сумма в уравнении (14) полностью совпадает с X_kпрямым дискретным преобразование Фурье (5). Таким образом, мы получаем формул для вычисления другой половины спектра

(15)

Таким образом, формулы (11) и (15) позволяют найти спектр сигнала, используя дискретное преобразование Фурье (5). Подведем итог в виде алгоритма вычисления спектра сигнала.

1. Имеем отсчеты дискретного сигнала.

2. Вводим последовательность x_n, связанную с отсчетами следующим образом.

Для примера, положимN = 6 и покажем соответствие между последовательностямиs_nиx_n.

3. Далее выполняем дискретное преобразование Фурье (5) над последовательностью x_nи получаем новую последовательность

4. Далее получаем не упорядоченный спектр

5. Получаем упорядоченный спектр по формулам

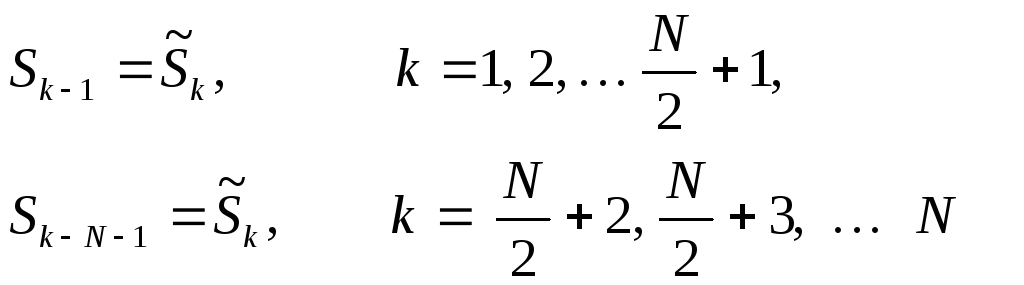
Для нашего примераN = 6 укажем соответствие между упорядоченным и не упорядоченным спектрами

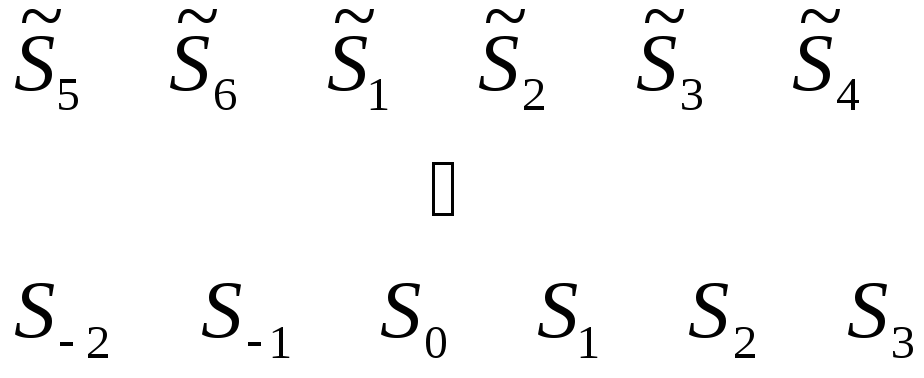
Замечание 1. Если сигналs( t ) вне интервала интегрированияTне равен нулю, то спектр будет вычисляться приближенно. Для улучшения результатов интервал интегрирования надо увеличить.

Замечание 2. Дискретное преобразование Фурье в нашей задаче появилось, когда интеграл Фурье мы стали вычислять приближенно по формуле прямоугольников. Поэтому точность вычисления зависит от шага дискретизации t. Чем меньше шаг, тем точнее результат.

Замечание 3. Дискретное преобразование Фурье мы используем для вычисления спектра финитных сигналов. Казалось бы, что для вычисления спектра периодических сигналов (которые являются инфинитными) этот способ не подойдет. Однако это не так. Этот метод прекрасно подходит для анализа спектра периодических сигналов. Более того, ДПФ был придуман для работы с периодическими сигналами. Ограничение только состоит в следующем. Данный метод позволяет описывать спектр таких сигналов, у которых частоты не превышают частоту Найквиста.

Порядок выполнения работы.

Работа состоит из трех частей. 1) Анализ спектра финитных сигналов: аналитический метод, метод ДПФ. 2) Нахождение базы финитного сигнала. 3) Анализ спектра сложного периодического сигнала.