13 Ортогональн Преобр Координат. Матрица преобразования.

Называется преобр. При котором отронорм мированный базис преходит в другой ортонорм базис.

e1e2e3= e`1e`2e`3 , где Cij – матрица ортогон преобр.

равен cos соответств угла между старой и новой СК.

Матрица преобразов.

Инверсия	Плоскость Симметрии прерпенд x3

Поповро вогруг оси на угол 

Cij=

X1	X2	X3

Обратное преобразование.

Cij`=(Cij)^-1=(Cij)^T (т.к. ортогональны)

Последовательное преобразование.

e1e2e3= e`1e`2e`3= e``1e``2e``3

;

C=C(5)C(4)C(3)C(2)C(1)

14. Тензорное описание свойств кристаллов. Скаляры векторы и тензоры

Как правило в следствии анизотропии св-в кристаллов явления вызванные в кристалле каким-либо воздействием не совпадают в общем случае по направлению с этим воздействием. В общем случае взаимосвязь между воздействием способным изм-ть какое-либо св-во кристалла и эффектом достигнутым, т.е реакцией можно записать

(эффект)=(свойство)×(воздействие). В зав-ти от сложности воздействия различают слдующие типы св-в

1. Если воздействие и вызванное явление изотропны, т.е не связаны с направлением, то и соответствующее св-во кристалла явл изотропным или математически говоря скалярно

Значение скаляра полностью задается одним числом и не изменяется при перобразовании координат

Скаляр-тензор нлевого ранга

(Плотность, теплоемкость, внутренняя энергия, энтрапия, коэф-т объемного температрного расширения)

ΔS=(C/T) ΔT ΔS скаляр

ΔS=(C/T) ΔT ΔT скаляр

Следовательно С-скаляр

Векторы- (тензоры первого ранга) опр-ся однозначно тремя координатами(проекции на оси)

(эффект)=(свойство)×(воздействие)

изотропное

вектор скаляр

векторное

К тензорам первого ранга относятся: напряжение эл. поля, градиент температуры, магн дипольный момент

При преобразовании координат векторы преобразуются следующим образом (x1,x2,x3)→(x1’,x2’,x3’) A_i’=СijAj

Cij

Пример. Пироэлектрический эффект состоит в возникновении или изменении диэлектрической поляризации при изменении температуры

ΔP=(P)ΔT ΔP-эффект(вектор) ,ΔT-воздействие(скаляр), =>(P)-свойство(вектор)

для высокосимметричных кристаллов

Тензор второго ранга

Девять величин Tij преобразующиеся при перходе от одной системы координат к лругой как произведение компонент 2ух векторов наз. тензором 2ого ранга

Преобразование ортогонально в любом случае

всего 9 слагаемых

Матрица преобразований Cij связывает компоненты одного и того же вектора в разных системах координат

Тензорная величина Tij задает компонеты вектора только в одной системе координат

В зависимости от соотношния тензора 2 ранга бывают

-симметричные тензоры 2 ранга(6 независимых компоннт) Tij=Tji

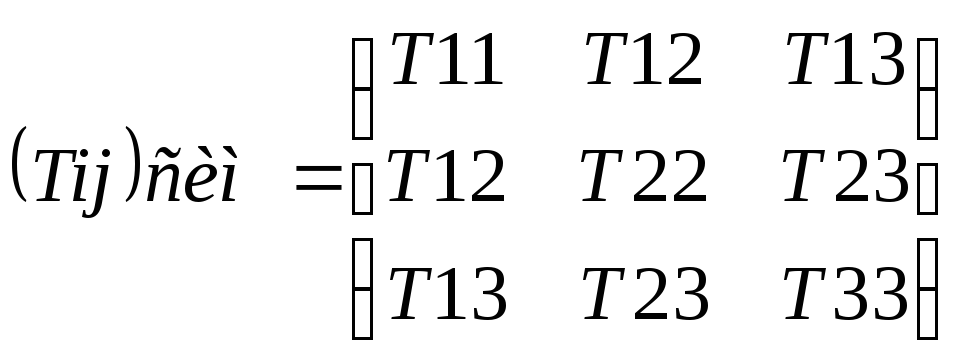
-антисимметричные(3 независимых компоненты) Tij= -Tji

Tij=-Tij≡0

Св-ва Tij

Тензора 2 ранга могут

1-связывать векторное воздействие и векторную реакцию

вектор=(св-во)×(вектор)

тензор 2 ранга(тензор диэл. Восприимчивости, диэл непроницаемости, теплового потока)

2Тензор 2ранга=(св-во)×(скаляр)

тензор 2 ранга(деформация при гидростатическом сжатии, тепловое расширение, термические напряжения)

Внешняя симметрия тензоров 2 ранга

А)для кубических кристаллов1 независимое значение

Б)для кристаллов тригональной гекса, тетра

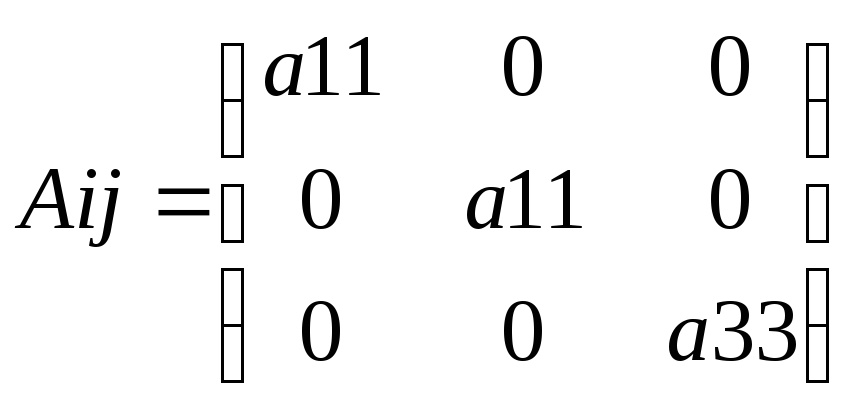2 независимых компоненты

в)ромбическая3 независ компоненты

триклинная 6 независ компонентaij=aji