8. S-m-n-теорема

В этом разделе мы докажем теорему, принадлежащую к числу основных результатов теории алгоритмов. Суть теоремы в следующем. Допустим, что f(х, у) - вычислимая функция. Для каждого фиксированного значения a переменной х функция f порождает одноместную вычислимую функцию g_a(y) = f(a, у). Из вычислимости функции g_a следует существование индекса b такого, что f(a, у) = f_b(у). Оказывается индекс b можно эффективно вычислить по параметру а.

Теорема 8.1 (s-m-n-теорема, простая форма). Пусть f(х, у) -вычислимая функция. Существует всюду определенная вычислимая функция s(x), такая, что f(х, у) = f_s(x)(у).

Доказательство. Из вычислимости функции f(х, у) следует существование МНР-программы Pr, которая, исходя из начальной конфигурации (x, y, 0, 0, ...), вычисляет значение функции f от двух аргументов х и у. Изменим программу Pr, добавив спереди команды, преобразующие начальную конфигурацию

R1	R2	R3	R4	...
y	0	0	0	...		(*)

в конфигурацию

R1	R2	R3	R4	...
a	y	0	0	...

следующим образом:

T(1, 2)

Z(1)

Pr

Новая программа Pr1, примененная к начальной конфигурации (*), вычисляет значение функции g_a(y) = f(a, у) от одного аргумента у.

Теперь рассмотрим функцию s(a) = (Pr1), сопоставляющую произвольному неотрицательному целому числу a геделев номер программы Pr1. Функция s всюду определена и по тезису Черча вычислима. Кроме того, по построению f_s(a)(у) = f(a, у) для каждого .

Замечание 8.1. Сформулированную теорему называют также теоремой параметризации, поскольку она позволяет по заданной вычислимой функции f(x, у) и фиксированному параметру a найти геделев номер s(a) программы, вычисляющей функцию f_s(a)(у) = f(a, у).

Доказанная выше теорема 8.1 является частным случаем более общей теоремы.

Теорема 8.2 (s-m-n-теорема). Пусть m, n – натуральные числа, - вычислимая функция с геделевым номеромa. Существует всюду определенная вычислимая функция такая, что

.

Доказательство сформулированного утверждения аналогично доказательству теоремы 8.1.

Замечание 8.2. Название теоремы 8.2 связано с обозначением для функций в формулировке теоремы.

Покажем теперь, как можно использовать s-m-n-теорему для доказательства неразрешимости проблем. s-m-n-теорема часто используется для сведения проблемы «» к другим проблемам.

Теорема 8.3. Проблема «» неразрешима.

Доказательство. Рассмотрим функцию

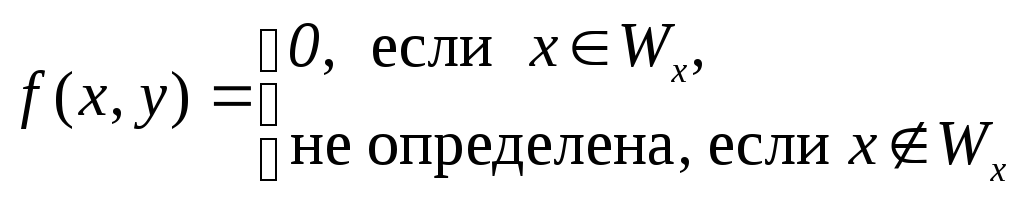
По тезису Черча функция f(x, y) вычислима. Отсюда по s-m-n-теореме вытекает существование всюду определенной вычислимой функции s(x) такой, что . По определению функции f(x, y) имеем:

.

Следовательно, истинность условия можно установить, определив справедливость равенства. Тем самым мы свели проблему «» к проблеме «». Поскольку первая из них неразрешима, то неразрешима и вторая.

Замечание 8.3. Теорема 8.3 показывает, что в области проверки правильности компьютерных программ имеются принципиальные ограничения. В ней говорится о том, что не существует алгоритма проверки того, будет ли программа вычислять нулевую функцию. Несколько изменив доказательство теоремы 8.3, можно убедиться в том, что то же самое справедливо и для любой другой конкретной вычислимой функции.

Теорема 8.4. Проблема неразрешима.

Доказательство. Допустим, что проблема разрешима. Тогда разрешима и проблема, гдеc – индекс функции 0 . Однако, это противоречит теореме 8.3. Таким образом, проблеманеразрешима.

Замечание 8.4. Из теоремы 8.4 следует, что вопрос о том, вычисляют ли две программы одну и ту же одноместную функцию, неразрешим. Важность этого результата для теоретического программирования очевидна.

Естественно задаться вопросом, какие свойства вычислимых функций можно алгоритмически распознать по их программам. Оказывается, что никакие, кроме тривиальных. Доказательство этого факта содержится в теореме Райса.

Теорема 8.5 (теорема Райса). Пусть B - непустое множество одноместных вычислимых функций, не совпадающее со всем множеством одноместных вычислимых функций. Тогда проблема «» неразрешима.

Доказательство. Очевидно, что проблема «» разрешима тогда и только тогда, когда разрешима проблема «». Поэтому без потери общности можно считать, что нигде не определенная функцияне принадлежитB.

Выберем некоторую функцию и рассмотрим функцию

По тезису Черча функция f(x, y) вычислима. Поэтому существует (по s-m-n-теореме) всюду определенная вычислимая функция s(x) такая, что . По определению функции f(x, y) имеем:

.

Таким образом, с помощью вычислимой функции s(x) мы свели проблему «» к проблеме «». Следовательно, проблема «» неразрешима.

Дадим более содержательную формулировку теоремы Райса. Пусть Q некоторое свойство одноместных вычислимых функций. Свойство Q назовем нетривиальным, если существуют функции, обладающие свойством Q, и функции не обладающие этим свойством.

Все обычно рассматриваемые свойства являются нетривиальными. Примерами нетривиальных свойств служат следующие:

• функция тождественно равна нулю;

• функция нигде не определена;

• функция всюду определена;

• функция взаимно однозначна;

• функция определена при x = 0.

Так как вычислимые функции могут быть заданы программами их вычисления, то естественно возникает вопрос: можно ли по программе узнать, обладает ли соответствующая ей функция заданным нетривиальным свойством.

Теорема 8.6. Каково бы ни было нетривиальное свойство Q одноместных вычислимых функций, задача распознавания этого свойства алгоритмически неразрешима.

Доказательство. Пусть B - множество одноместных вычислимых функций, обладающих свойством Q. Множество B не пусто и не совпадает со всем множеством одноместных вычислимых функций. По теореме Райса проблема «» неразрешима.

Из последней теоремы следует неразрешимость многих задач, связанных с программированием. Например, если имеется некоторая программа, то по ней, вообще говоря, ничего нельзя сказать о функции, реализуемой программой. По двум программам нельзя установить, реализуют ли они одну и ту же функцию, а это приводит к неразрешимости многих задач, связанных с эквивалентными преобразованиями и минимизацией программ. В любом алгоритмическом языке, какие бы правила синтаксиса там ни применялись, всегда будут иметься «бессмысленные» программы, задающие функции не определенные ни в одной из точек (эти программы нельзя обнаружить). Теорема Райса позволяет доказывать алгоритмическую неразрешимость многих задач, связанных с вычислениями на компьютерах.

Методология программирования включает следующие компоненты - это наука, техника (ремесло) и искусство.

На этапе проектирования программирование требует от программиста немалой изобретательности. Проект программы - это практически изобретение, произведение искусства, а этому вряд ли можно научить. Но программирование - это одновременно и техническая задача, для решения которой формулируются технологические правила, представляющие собой эмпирически найденные правила хорошего программирования. Эти правила передаются от мастера к ученикам. Однако программирование — это наука. Наука показывает, как можно достичь множества целей, применяя строго определенные правила построения к основным конструктивным элементам. Наука демонстрирует, какие свойства программы выводимы из свойств, подразумеваемых у ее составляющих.

Необходимость и возможность создания математической теории программирования были провозглашены в первые годы развития вычислительных машин. Это объясняется отчасти тем, что первыми программистами были математики и среди них - видные ученые.

Выделим три основных аспекта программирования, где используются математические модели программ.

Разработка логических основ составления и проверки программ. Процесс систематического конструирования программ сопровождается формулированием точных математических утверждений о событиях, происходящих при выполнении программы. При этом предполагается, что построенная одновременно с программой последовательность логических умозаключений будет служить доказательством правильности решения поставленной задачи.

Задачи обоснования алгоритмов трансляции. Надо уметь доказывать, что применяемые в трансляторах оптимизирующие преобразования программ не нарушают правильность работы программ. Исследования по теории трансляции показывают, что генерация объектного кода может быть формально выведена из семантики входного языка, представленной в некоторой математической модели.

Методы параллельного программирования. Методы составления программ для многопроцессорных вычислительных систем могут быть построены только на основе точных математических моделей, поскольку человек не в состоянии достоверно проследить все тонкости совместного выполнения параллельных вычислительных процессов.

"Правильность программ" — термин неоднозначный. Под правильностью программ понимают:

* отсутствие ошибок в программе;

* соответствие программы ее спецификации;

* возможность формального вывода программы из формального набора предпосылок.

Термин "правильность программ" стал популярным одновременно с терминами "структурированное программирование" и "технология программирования".

К такому методу доказательства правильности программ относится метод индуктивных утверждений, независимо сформулированный К. Флойдом и П. Науром.

Суть этого метода состоит в следующем:

1) формулируются входное и выходное утверждения: входное утверждение описывает все необходимые входные условия для программы (или программного фрагмента), выходное утверждение описывает ожидаемый результат;

2) предполагая истинным входное утверждение, строится промежуточное утверждение, которое выводится на основании семантики операторов, расположенных между входом и выходом (входным и выходным утверждениями); такое утверждение называется выведенным утверждением;

3) формулируется теорема (условия верификации):

из выведенного утверждения следует выходное утверждение;

4) доказывается теорема; доказательство свидетельствует о правильности программы (программного фрагмента).

Доказательство проводится при помощи хорошо разработанных математических методов, использующих исчисление предикатов первого порядка.

Введем обозначение { Q } S { R }, (3.1) где Q, R-предикаты,S-программа (оператор или последовательность операторов). Обозначение определяет следующий смысл: "Если выполнение S началось в состоянии, удовлетворяющем Q, то имеется гарантия, что оно завершится через конечное время в состоянии, удовлетворяющем R". Предикат Q называетсяпредусловиемили входным утверждением S, предикат R -постусловиемили выходным утверждением. Следовательно, R определяет то, что нужно установить. Можно сказать, что R определяет спецификацию задачи. Отметим, что (3.1) - предикат, т.е. предложение, которое либо истинно, либо ложно. Конечно, нам нужно, чтобы он был истинен. Наша цель - при написании программы некоторым способом доказать истинность (3.1). Для этого нужно уметь записывать (3.1) в исчислении предикатов и формально доказывать его истинность. Будем называть предикат, помещенный в программу,утверждением. Утверждается, что он истинен в соответствующий момент выполнения программы. В предусловии Q нужно отражать тот факт, что входные переменные получили начальные значения. Для обозначения начальных значений будем использовать большие буквы ([7]).

Пример 1. Пусть надо определить приближенное значение квадратного корня: s = sqrt(n), где n<=0, n, s принадлежат классу целых неотрицательных чисел. Определим постусловие в виде : R: s*s<=n < (s+1)*(s+1).

Пример 2. Даны целочисленные n>0 и массив a[1..n]. Отсортировать массив, т.е. установить

Пример 3.Определить x как максимальное значение массива a[1..n]. Определим постусловие в виде:

Пример 4. Пусть имеем программу обмена значениями двух целых переменных a и b: S: r := a; a := b; b := r Сформулируем входное и выходное утверждения программы и представим программу S в виде предиката (3.1): { a = A and b = B } S { a = B and b = A }, где A, B - конкретные значения переменных a, b. Программа вместе с утверждениями между каждой парой соседних операторов называетсянаброском доказательства. Последовательно, для каждого оператора программы формулируя предикат (3.1), можно доказать, что программа удовлетворяет своим спецификациям. Представим набросок доказательства для программы S: { a = A and b = B }; r := a; { r = a and a = A and b = B }; a := b; { r = a and a = B and b = B }; b := r; { a = B and b = A } Не обязательно набросок доказательства должен быть настолько полным. Для документирования программы нужно вставить достаточно утверждений, чтобы программа стала понимаемой. Программа, содержащая утверждения для ее документирования, называетсяаннотированной программой.Чтобы использовать утверждения для доказательства правильности программы, необходимы правила. Введем правила К.Хоара и Э.Дейкстра.

Основой для исчисления выводов программ служат правила К.Хоара (правила верификации) для интерпретации программных конструкций. Сформулируем правила (аксиомы) К.Хоара, которые определяют предусловия как достаточные предусловия, гарантирующие, что исполнение соответствующего оператора при успешном завершении приведет к желаемым постусловиям.

A1.Аксиома присваивания: { Ro } x := e { R }

Неформальное объяснение аксиомы: так как x после выполнения будет содержать значение e, то R будет истинно после выполнения, если результат подстановки e вместо x в R истинен перед выполнением. Таким образом Ro = R(x) при x = e. Для Ro вводится обозначение: Ro=R^x_e(у Вирта) или R_x->e(у Дейкстры) что означает, что x заменяется на e. Аксиома присваивания будет иметь вид: { R^x_e} x:=e {R} Сформулируем два очевидных правила.

A2.Если известно: { Q } S { P } и { P } => { R }, то { Q } S { R }

A3.Если известно: { Q } S { P } и { R } => { Q }, то { R } S { P }

Пусть S - это последовательность из двух операторов S1;S2 (составной оператор).

A4.Если известно: { Q } S1 { P1 } и { P1 } S2 { R }, то { Q } S { R }. Очевидно, что это правило можно сформулировать для последовательности, состоящей из n операторов.

Сформулируем правило для условного оператора (краткая форма).

A5.Если известно: { Q and B } S1 { R } и { Q not B } => { R },то { Q } if B then S1 { R }. Правило A5 соответствует интерпретации условного оператора в языке программирования.

Сформулируем правило для альтернативного оператора (полная форма условного оператора ).

A6. Если известно: { Q and B } S1 { R } и { Q not B } S2 { R },то { Q } if B then S1 else S2 { R }.

Сформулируем правила для операторов цикла. Предусловия и постусловия цикла until (до) удовлетворяют правилу: A7.Если известно: { Q and not B } S1 { Q } , то { Q } repeat S1 until B { Q and not B }

Правило вводит важное понятие инварианта цикла. Предикат Q, истинный перед выполнением и после выполнения каждого шага цикла, называется инвариантным отношениемили простоинвариантом цикла. В математике термин "инвариантный" означает не изменяющийся под воздействием совокупности рассматриваемых математических операций. В данном случае единственная операция - это выполнение шага цикла при условии истинности Q вначале. Предусловия и постусловия цикла while (пока) удовлетворяют правилу:

A8.Если известно: { Q and B } S1 { Q } , то { Q } while B do S1 { Q and not B }

Правила A1 - A8 можно использовать для проверки согласованности передачи данных от оператора к оператору, для анализа структурных свойств текстов программ, для установления условий окончания цикла. Кроме того, правила можно использовать для анализа результатов выполнения программы, что связано с семантикой программы.

Пример 5. Пусть надо определить частное q и остаток r от деления x на y.Входные данные:x, y принадлежат классу целых неотрицательных чисел, причем y > 0.Выходные данные:q, r принадлежат классу целых неотрицательных чисел.Описание алгоритма

Задать(x,y); /* x,y получают конкретные значения X,Y */ r := x; q := 0; while y <= r do begin r := r - y; q := q + 1 end; выдать(q,r);

Сформулируем постусловие R:(r < y) and (x = y*q + r) Нужно доказать, что { y > 0 and x і y } S { (r < y) and (x = y*q + r )}

Доказательство.1. Очевидно, что Q => x = x + y * 0. 2. Применим аксиому A1 к оператору r := x, тогда получим { x = x + y * 0 } r := x { x = r + y * 0 } 3. Аналогично, применяя A1 к оператору q := 0, получим: { x = r + y * 0 } q := 0 { x = r + y*q } 4. Применяя правило A3 к результатам пунктов 1 и 2, получим { Q } r := x { x = r + y * 0 } 5. Применяя правило A4 к результатам пунктов 4 и 3, получим { Q } r := x; q := 0 { x = r + y*q } 6. Выполним равносильное преобразование x = r + y * q and y< =r= > x = (r - y) + y*(q + 1) 7. Применяя правило A1 к оператору r := r - y, получим {x = (r - y) + y*( q + 1)} r := r - y {x = r + y*(q + 1)} 8. Для оператора q := q + 1 аналогично получим { x = r + y*(q + 1) } q := q + 1 { x = r + y*q } 9. Применяя правило A4 к результатам пунктов 7 и 8, получим { x = (r - y) + y*( q + 1) } r := r - y; q := q + 1 { x = r + y*q } 10. Применяя правило A2 к результатам пунктов 6 и 9, получим { x = r + y*q and y <= r } r := r - y; q := q + 1 { x = r + y*q } 11. Применяя правило A8 к результату пункта 10, получим { x = r + y*q } while y <= r do beqin r := r - y; q := q + 1 end { not (y <= r) and (x = r + y*q) } Утверждение x = r + y*q является инвариантом цикла, так как значение его остается истинным до цикла и после выполнения каждого шага цикла. 12. Применяя правило A4 к результатам пунктов 5 и 11, получаем то, что требовалось доказать, т.е. { Q } S { not (y <= r) and (x = r + y*q) } Осталось доказать, что выполнение программы заканчивается. Доказывать будем от противного, т.е. предположим, что программа не заканчивается. Тогда должна существовать бесконечная последовательность значений r и q, удовлетворяющая условиям 1) y <= r ; 2) r, q принадлежат классу неотрицательных целых чисел. Но значение r на каждом шаге цикла уменьшается на положительную величину: r := r - y (y > 0). Значит, последовательность значений r и q является конечной, т.е. найдется такое значение r, для которого не будет выполняться условие y <= r и циклический процесс завершится.

Приведенный процесс доказательства правильности не убеждает нас в полезности, так как он занимает больше строк, чем сама программа. Но "подобные доказательства для программ обладают всеми свойствами элегантных математических построений, которые, оказываясь на нужном месте приобретают неожиданно значение"([9]). В следующем примере не будем так подробно останавливаться на интерпретации каждого оператора программы.

Пример 6.Пусть нужно вычислить z = a^b.Входные данные:a принадлежит классу вещественных чисел, b принадлежит классу неотрицательных целых чисел.Выходные данные:z принадлежит классу вещественных чисел. Сформулируем Q, R: Q: b >= 0 R: z = a^bОпишем алгоритм вычисления, из которого трудно понять, что он определяет и правильно ли определяет.Описание алгоритма SЗадать(a,b); x := a; n := b; z := 1; while n <> 0 do if even(n) then begin n := n div 2; x := x*x end else begin z := z*x; n := n - 1 end; выдать(z); Нужно доказать: { b >=0 } S { z = a^b} Построим инвариант цикла: P: n >= 0 and z*xⁿ= a^bОчевидно, что P истинно после инициализации переменных x, n, z. В этом легко убедиться, подставив значения перечисленных переменных в предикат P. Значит, P истинно до выполнения цикла. Проверим, остается ли P истинным после выполнения каждого шага цикла. Для этого необходимо проверить два случая: n - четное число и n - нечетное число. При n четном имеем: 1) значение z не меняется; 2) значение n становится равным n div 2 ; 3) значение x становится равным x*x. Вычислим предикат P при этих значениях, получим (n div 2)>= 0 and z*(x*x)^{n div 2}= a^b. Это выражение равносильно предикату P, так как n - четно. При n нечетном имеем: 1) значение z становится равным z*x; 2) значение n становится равным n-1; 3) значение x не меняется. Вычислим предикат P при этих значениях, получим n-1 >=0 and z*x*x^n-1= a^b. Это выражение равносильно предикату P, так как n - нечетно. Вычислим предикат P после выполнения цикла (в этом случае n = 0), получим 0 >= 0 and z*x⁰= a^b, что доказывает истинность P после выполнения цикла. Кроме того, полученное утверждение равносильно постусловию R. Завершение алгоритма очевидно.