16

Определение 3.1. Пусть f - функция от n неотрицательных целых переменных со значениями во множестве Z₀ неотрицательных целых чисел (функция ). Функцияf называется вычислимой на МНР (или МНР–вычислимой), если существует такой алгоритм P, что

1) вычисление P(a₁, a₂, ..., a_n) останавливается тогда и только тогда, когда (a₁, a₂, ..., a_n) принадлежит области определения f;

2) если (a₁, a₂, ..., a_n) принадлежит области определения f; то в заключительной конфигурации в регистре R₁ находится целое число b такое, что f(a₁, a₂, ..., a_n) = b.

С этого момента под термином вычислимоебудем подразумевать МНР–вычислимое.

Возникает теперь вопрос: насколько хорошо неформальное интуитивное понятие вычислимой функции отражено в различных формальных описаниях? Этот вопрос подвергался математиками серьезному обсуждению, в результате которого было высказано утверждение, известное под названием «тезис Черча»: каждая функция, вычислимая посредством процесса, алгоритмический характер которого интуитивно ясен, является вычислимой функцией. Применительно к нашему изложению этот тезис можно перефразировать следующим образом: всякая функция, для которой существует алгоритм (в интуитивном смысле) вычисления ее значений, является МНР-вычислимой функцией.

Сразу же заметим, что это утверждение не является теоремой, подлежащей математическому доказательству; оно имеет статус утверждения, принимаемого как постулат, справедливость которого подтверждается рядом свидетельств. Во-первых, таким свидетельством является то, что, как уже отмечалось, многие независимые уточнения интуитивного понятия вычислимой функции привели к одному и тому же классу функций. Во-вторых, никому не доводилось найти функцию, которую можно признать вычислимой в интуитивном смысле и которая не была бы МНР-вычислимой. Исходя из этих соображений и собственного опыта, большинство математиков приняли тезис Черча.

Начнем с двух выдающихся открытий, сделанных в конце XIX в. немецким математиком Георгом Кантором: диагонального процесса и доказательства несчетности множества всех действительных чисел. Эти открытия стимулировали развитие математики на весь ХХ век и до настоящего времени. Теория алгоритмов тоже родилась как следствие проблем, теорией множеств, а диагональный процесс оказался излюбленным методом математиков. Все началось с парадоксов теории множеств.

Далее рассмотрим парадокс Рассела и его связь с диагональным процессом.

Бертран Рассел (1872—1970) — выдающийся логик, философ, математик и социолог, лауреат Нобелевской премии по литературе (1950). Не будет большим преувеличением сказать, что наибольшую известность среди самого широкого круга людей ему принесли не его многочисленные математические и философские работы, а всего лишь одна логическая головоломка — "парадокс деревенского брадобрея".

Парадокс Рассела (точнее, Рассела — Цермело), по словам Гильберта, оказался катастрофой для математиков. Над его разрешением, так же, как и над разрешением других найденных парадоксов канторовской теории множеств, трудились самые выдающиеся математики тех-лет, и, собственно говоря, описание Тьюрингом своей "машины" в 1936 г. в известном смысле находилось в "струе" решений тех логико-математических проблем, которые исследовались в связи с парадоксами теории множеств.

опишем его популярную форму, которую придумал сам Рассел в 1919 г. [2].

В некоторой деревне живет брадобрей, который объявил, что он бреет всех жителей деревни, которые не бреются сами, но, разумеется, не бреет тех жителей, которые бреются сами. (Математик выразил бы это правило так:

"Брадобрей бреет тех и только тех жителей деревни, которые не бреются сами".) Однажды брадобрей задумался: должен ли он брить самого себя ? Если он будет брить себя, то, поскольку он бреет только тех, кто не бреется сам, он не должен себя брить. Если же он не будет бриться сам, то тогда он должен себя брить... Он оказался в безвыходном положении — он не мог ни брить себя, ни не брить.

Этот парадокс оказывается тесно связанным с канторовским диагональным процессом. Пусть п— число жителей деревни. Занумеруем каждого жителя деревни числами от 1 доп.Нарисуем квадратную таблицу изпстрок ипстолбцов. В каждой клетке таблицы поставим крестик или нолик по следующему правилу: если житель номерi бреет жителя номерj, то в клетке, находящейся в строке номерiи столбце номерj, поставим крестик, иначе — нолик. Может получиться, скажем, таблица, изображенная нарис. 1а(в случаеп= 5; согласно этой таблице, например, житель номер 3 бреется сам, но не бреет жителя номер 5).

Рис.1

Эту таблицу представим в виде двухмерного массива Т, т.е. пустьT[i, j] — это элемент таблицы (крестик или нолик), находящийся в строке номерiи столбце номерj. Пусть также D— одномерный массив длиныпзаполненный крестиками и ноликами следующим образом: если наш Брадобрей бреет жителя номер i, тоD[i] — крестик, иначе— нолик. (Как обычно,D[i] обозначает i-й элемент массиваD. Структура массиваDпоказана нарис. 16.)Правило "Брадобрей бреет тех и только тех жителей деревни, которые не бреются сами", можно выразить так:

 iD[i]Т[i, i] (*)

При нашей нумерации жителей деревни Брадобрей тоже должен был получить какой-то номер. Какой? Если его номер, скажем, i, то тогда, согласно правилу построения таблицы Т,массивDдолжен был быцеликом совпадать со строкой номерiтаблицыТ. Другими словами, должно быть:

j D[j]=T[i, j]

Но это невозможно: если в предыдущем равенстве положить jравнымi, то получитсяD[i] = Т[i,i] — противоречие с требованием (*). Из требования (*) следует, что строкаDне может совпадать ни с одной из строк таблицы Т.

Требование (*) составляет "соль" канторовского диагонального процесса.

Тьюринговская проблема остановки

Теперь мы разберем так называемую "проблему остановки", которая оказывается также тесно связанной с канторовским диагональным процессом.

Проблема зацикливания в в МНР и стандартном программировании.

Примером "бесконечного цикла" может служить такой фрагмент программы на Паскале:

х:= 1; Repeat { какие-то действия, которые не изменяют значение переменной x. };Untilx>10

Такой фрагмент вполне мог бы возникнуть из-за невнимательности программиста.

Зададимся следующим вопросом. Нельзя ли определить программным способом, с помощью самого компьютера, "зациклится" ли данная программа? Может быть, можно написать некоторую универсальную программу (обозначим ее через U), которая принимала бы на входтекстзаданной программы, анализировала его и выдавала бы ответ, "зациклится" эта программа или нет.

Возможность написания программы Uкажется правдоподобной: ведь если мы подозреваем какую-то нашу программу на "зацикленность", мы анализируем ее текст, запускаем трассировку (пошаговую отладку), наблюдая, "что происходит внутри программы".

Программа Uмогла бы стать "надстройкой" над компилятором, которая "вылавливала" бы ошибку особого рода — ошибку "бесконечного цикла".

Уточним формулировку задачи.Каждая программаПв каждом конкретном случае работает со входными данными. (Строго говоря, некоторые программы, например какая-нибудь программа вычисления числапис точностью до 100 000 знаков, могут и "ничего не получать на вход" — в этом случае будем считать, что входные данные для такой программы образуют "пустой набор", файл из нуля байт.) Можно считать, что эти входные данные берутся всегда из какого-то файлаД. Может случиться, что некоторая программа, получая на вход одни данные, "зацикливается", а получая другие — нет. (Например, если бы во фрагменте программы на Паскале, приведенном выше, вместо присваивания х:= 1 стоял бы вызов процедуры чтения Readln (х), то при вводе "1" программа бы зациклилась в этом месте, а при вводе "12" — нет.)

Работу программы Uможно спроектировать следующим образом. ПрограммаUдолжна получать на вход, во-первых, текст программыП(текстовый файл), а во-вторых, некоторый файл с даннымиД. Затем она должна проанализировать эти два файла и выдать точный ответ, "зациклится" ли программа П,еслиПполучила на вход файлД. Можно всегда считать, что программаUможет воспринимать на входлюбыефайлы: например, если файлПне является синтаксически правильной программой на выбранном языке программирования (скажем, Паскале), то программаUэто легко определяет, но все равно считает, что в этом случаеПявляется "программой": например, такой, которая "ничего не делает" и, следовательно, не "зацикливается". Соответственно, если файлДимеет "неправильный формат" (например, на вход программеПтребуется число, а в файлеДимеется что-то другое), то программаПвсегда останавливается на этих "неправильных данных". Итак, вот более точное описание нашего проекта:

а) программа Uчитает два произвольных файла:ПиД;

6) если файл Псодержит синтаксически правильную программу (для определенности - на Паскале), а файлДпредставляет собой подходящие данные для программыП, то программаUпроверяет, "зациклится" ли Пна данныхД. Если она зациклится, то на экран компьютера будет выдано сообщение "зациклится", иначе — "не зациклится";

в) если файлы ПиДне удовлетворяют условиямб, то на экран выдается сообщение "не зациклится" (и в этой ситуации для простоты, мы все равно называем П"программой", аД— "данными", иПв этом случае не "зацикливается" наД"по определению" ).

Будем считать, что для работы программы Uв нашем распоряжении имеется "идеальный" компьютер без обычных ограничений на объем памяти (т.е. при любом вычислении на этом компьютере можно выделить любой необходимый объем памяти, компьютер способен работать со сколь угодно большими данными). Забудем даже о любых соображениях эффективности – нам абсолютно все равно, как долго будет работать программа U,лишь бы в конце концов она выдала ответ. Таким образом, мы интересуемся только теоретической, принципиальной возможностью написания программы U.

Предположим, что нам удалось написать такую программу U. Можно считать, что она тоже написана на Паскале. Теперь мы собираемся написать новую программу, которую обозначим через U1.Но прежде мы введем специальное понятие –стандартный номер файла. Любой файл можно представить как "слово", быть может, очень длинное. Каждая "буква" этого слова берется из некоторого "алфавита". Например, в соответствии с архитектурой "привычных" нам на сегодняшний день компьютеров, можно считать, что алфавит для таких "слов" состоит из 256 символов, а каждая буква в "слове" – это один байт в файле; в качестве "букв" здесь выступают все символы – "настоящие буквы", знаки препинания, пробел, специальные символы и т.д. Можно и по-другому. Каждый байт в файле определяется двумя шестнадцатеричными цифрами (от 0 до F). Тогда наш алфавит состоит из 16 "букв": 0, 1, ..., А, В, С, D, Е, F. Любой файл можно себе представить как некоторую последовательность этих символов, т.е. как слово из букв этого алфавита. В любом случае все файлы могут быть расположены в некоторую бесконечную последовательность:

Ф₁, Ф₂, Ф₃, Ф₄.... (**)

(Сначала идет "пустой файл", в котором нет ни одного байта. Затем перечисляются в "алфавитном порядке" все файлы состоящие из одной "буквы", затем — состоящие из двух "букв", и т.д.) В этой последовательности каждыйфайл получает некоторый номер. Этот номер мы и назовемстандартным номером файла.Будем считать, что мы зафиксировали какой-то из этих способов.

Ясно, что можно написать программу, которая по заданному файлу вычислит стандартный номер этого файла. Можно также написать программу, которая по заданному числу восстанавливает файл, стандартный номер которого равен n(это, впрочем, немного сложнее).

Итак, любойфайл попадает в последовательность (**) и имеет в ней свой уникальный номер, который мы называем стандартным номером этого файла. Значит, и у любого файла с программой (П), и у любого файла данных (Д) есть свои стандартный номер.

Теперь можно написать программу U1,которая будет, делать следующее:

1) получать на вход натуральное число i

2) восстанавливать файл Ф_iиз последовательности (**), т.е. восстанавливать файл со стандартным номеромi;

3) запускать программу U, подавая ей на вход в качестве файлаПфайл Фi., а в качестве файлаД— тот же самый файл Ф_i.

Коротко работу программы U1можно описать так: по заданному числуiона определяет, "зациклится" ли программа, реализованная в файле со стандартным номеромi при работе с данными, записанными в файле, который имеет стандартный номерi.

Ясно, что программу U1всегда можно написать так, чтобы она заканчивалась строками:

if z=0 then

(A) Writeln("He зациклится")

else

Writein("зациклится");

(в самом конце работы некоторая переменная z получает значение 0 или 1, и в соответствии с этим значением выдается одно из двух сообщений). Теперь подвергнем программу U1маленькой переделке. Фрагмент, приведенный выше, заменим на такой:

if z=0 then

(Б) Repeat Until 2=3

ElseWritein("зациклится");

Эту программу (назовем ее U2)сохраним в другом файле. Что делает U2?Она тоже, как и U1,получает на вход числоi, но отличается от U1вот чем: если выяснилось, что исследуемая программа со стандартным номеромiне "зацикливается" на файле данных со стандартным номеромj,то сама U2"зацикливается", а в противном случае U2выдает сообщение "зациклится" и после этого завершает работу.

Программа U2сама, конечно, записана в файле. Этот файл обязательно находится в последовательности (**) и имеет некоторый стандартный номер. Пустьk– этот номер. Что произойдет, если на вход программе U2в качестве числаiмы подадим числоk? В этом случае, конечно, выполнение программы U2может либо "зациклиться", либо остановиться. Предположим, что оно остановится. Тогда, как только компьютер дойдет до выполнения фрагмента (Б), переменная z должна получить нулевое значение (вспомним, как была написана программа U2,см. также фрагмент (А) ). После этого, в соответствии с (Б), произойдет "зацикливание". Предположив, что выполнение остановится, мы выяснили, что выполнение зациклится! Это невозможно. Теперь предположим, что выполнение зациклится. Но тогда программа U2,как говорилось выше, должна выдать сообщение "зациклится" и после этого остановиться. Это тоже невозможно.

Эта парадоксальная ситуация нам уже знакома: она удивительно похожа на ситуацию с Брадобреем. Почему мы оказались в ней – программа должна "зациклиться", если она остановится, и должна остановиться, если она "зациклится" ? В чем тут дело? Конечно же, в том, что мы предполагали возможность написания универсальной программы U,которая определяла бы любую программу на возможность "зацикливания". Итак, такой программыUне существует в принципе, или, как говорят математики,проблема остановки алгоритмически неразрешима.(Проблема остановки — это и есть то, чем мы занимались: существует ли программа, которая по заданным программе и данным для нее определяла бы, остановится ли эта программа при получении этих данных?)

Осталось еще отметить связь наших рассуждений с канторовским диагональным процессом. Вспомним про массив-таблицу Ти массив-строкуD. ЗдесьT[i,j] — крестик, если программа, реализованная в файле со стандартным номеромi, "зацикливается" на данных, расположенных в файле со стандартным номеромj, иначе — нолик. ЗначенияT[i,j] для любых заданныхiиjмогла бы вычислять, после небольших модификаций, программаU(если бы, конечно, она существовала). ЗначениеD[i] — нолик, если программа, реализованная в файле со стандартным номеромi, "зацикливается" на данных, расположенных в файле со стандартным номеромi, иначе – крестик. ЗначенияD[i] можно было бы вычислять, используя программу U1.Тогда дляТиDвыполняется требование (*) иDне совпадает ни с одной строкой таблицыТ.

Неразрешимость проблемы остановки впервые была доказана Аланом Тьюрингом в его работе, опубликованной в 1936 г. Конечно, тогда не было никаких компьютеров и тем более языков программирования, да и сам Тьюринг в той работе даже не пользовался термином "программа". Но его изложение, по сути, мало чем отличалось от нашего. Мы использовали язык Паскаль и говорили о "привычных" нам компьютерах, однако ясно, что эти подробности (о файлах, о конкретном языке программирования) были совсем не важны: существо наших рассуждении было чисто логическим.

***

Определение 4.1. Множество X называют счетным, если можно установить взаимно однозначное отображение между множеством неотрицательных целых чисел Z₀ и множеством X.

Определение 4.2. Множество называют не более чем счетным, если оно счетно или конечно.

Определение 4.3. Перечислением или нумерацией множества X называется отображение множества Z₀ на множество X.

Перечисление f определяет на множестве X некоторую бесконечную последовательность элементов изX такую, что каждый из элементов множества X встречается в этой последовательности, по крайней мере, один раз.

Если отображение f - взаимно однозначно, то f называют перечислением или нумерацией без повторений.

Определение 4.4. Множество X называется эффективно счетным, если существует функция , устанавливающая взаимно однозначное соответствие между множествами Z₀ и X такая, что f и f^--1 - вычислимые функции.

Теорема 4.1. Следующие множества являются эффективно счетными:

а) ;

б) ;

в) - множество всех конечных последовательностей целых неотрицательных чисел.

Доказательство. а) Докажем сначала эффективную счетность множества , состоящего из упорядоченных пар (x, y) с целочисленными неотрицательными компонентами x и y. Геометрически это множество представляет целочисленную решетку (рис. 4.1).

Рис. 4.1. Целочисленная решетка

Перенумеровать точки этой решетки можно различными способами, например, так, как показано на рисунке 4.2.

Предложенная нумерация устанавливает взаимно однозначное отображение между множествамии. Алгоритмический характер процесса вычисления значений функцииочевиден. Следовательно, по тезису Черча- вычислимая функция.

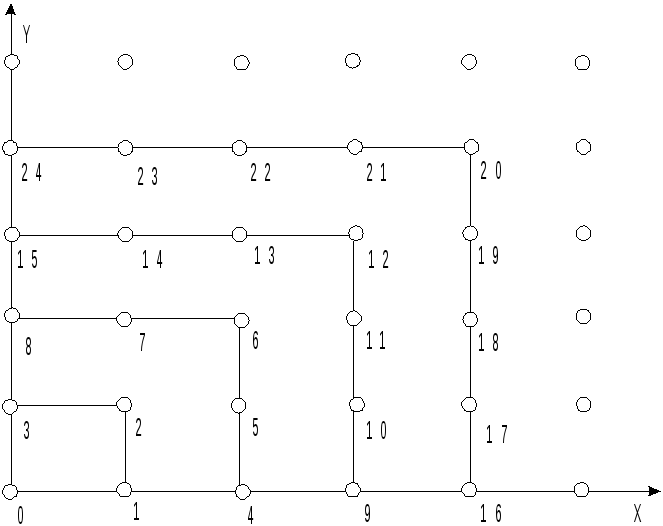
Рис. 4.2. Нумерация точек целочисленной решетки

Для вычисления значений обратной функции можно, например, в соответствии с предложенным алгоритмом последовательно нумеровать точки целочисленной решетки до номераz. Пара (x, y) координат точки с номером z является значением обратной функции . По тезису Черча- вычислимая функция.

Таким образом, множество эффективно счетно.

б) Теперь несложно доказать эффективную счетность множества . Для этого определим взаимно однозначное отображениемножестваупорядоченных троек неотрицательных целых чисел на множествоследующим образом. Из вычислимости функцийивытекает вычислимость функцийи. Поэтому множествоэффективно счетно.

в) Для доказательства эффективной счетности множества всех конечных последовательностей целых неотрицательных чисел рассмотрим функцию

,

сопоставляющую каждому упорядоченному набору (a1, a2, ..., ak) из k неотрицательных целых чисел некоторое неотрицательное целое число.

Для доказательства взаимной однозначности функции используем тот факт, что у каждого целого числа имеется ровно одно представление в двоичной системе счисления. Запишем значение функциив двоичной системе счисления:

(*)

Например,

= = 616 – 1 = 615;

= 2320 –1 = = 2319;

= 544 –1 = 543;

= 520 – 1 = 519;

= 3 – 1 = 2;

= 32 – 1 = 31;

= 1 – 1 = 0.

Однозначность отображения следует из того, что

.

Так как, кроме того, для любого неотрицательного числа x существует, очевидно, кортеж (c1, c2, ..., cn) такой, что , то функцияустанавливает взаимно однозначное соответствие между множествоми множеством.

Покажем, как вычисляются значения обратной функции для произвольного неотрицательного числаx.

В соответствии с формулой (*)

,

где - запись числаx + 1 в двоичной системе счисления.

Например,

;

;

;

;

;

;

;

.

В силу тезиса Черча функции ивычислимы. Следовательно,- эффективно вычислимое множество.

Теорема 4.2. Множество K команд МНР эффективно счетно.

Доказательство. Множество K команд МНР включает четыре типа команд Z(n), S(n), T(m, n), J(m, n, q), где . Определим взаимно однозначное отображение следующим образом:

(Z(n)) = 4  (n - 1);

(S(n)) = 4  (n - 1) + 1;

;

,

где - отображения, определенные в теореме 4.1.

Так как функции , очевидно, вычислимы, то отсюда вытекает эффективная счетность множестваK команд МНР.

Теорема 4.3. Множество P всех программ для МНР эффективно счетно.

Доказательство. Пусть - произвольная программа для МНР. Определим взаимно однозначное отображение следующим образом:

.

где - отображения, определенные в теореме 4.1. Так как функции, очевидно, вычислимы, то отсюда вытекает эффективная счетность множестваP всех программ для МНР.

Разумеется, существует много других отображений из P в , устанавливающих эффективную счетность множестваP. Для нашего изложения подходит любое из таких отображений. Зафиксируем одно из них, например, то которое описано в теореме 4.3.

Определение 4.5. Число (P) называется геделевым номером программы P или просто номером программы P.

Отображение  играет важную роль в теории алгоритмов. Название числа (P) связано с именем К. Геделя, впервые в 1931 году предложившего идею кодирования нечисловых объектов натуральными числами.

Ниже программу P с геделевым номером n будем обозначать . Из взаимной однозначности отображения следует при, хотя обе эти программыимогут вычислять одну и ту же функцию.

Пример 4.1. Найдем геделев номер программы P:

,

,

вычисляющей функцию f(x) = x + 2.

.

(S(1)) = 4  (1 - 1) + 1 = 1;

.

Пример 4.2. Вычислим программу по ее геделеву номеруm.

1) m = 0.

; .

Следовательно,

: 1. Z(1).

2) m = 1.

; .

Следовательно,

: 1. S(1).

3) m = 2.

; .

Следовательно,

: 1. Z(1),

2. Z(1).

4) m = 3.

; .

Следовательно,

: 1. T(1, 1).

Заметим, что различные программы ивычисляют одну и ту же функциюf(x) = 0.