
Обработка изображений / Л.Р. по обработке изображений Ч. 2
.pdfжающих его пикселов. Объекты представляют собой восьмисвязные либо четырехсвязные области единиц. Объект называется четырехсвязным, если для каждого пиксела объекта среди квартета соседних пикселов существует хотя бы один, равный 1 и принадлежащий этому же объекту. Объект называется восьмисвязным, если для каждого пиксела объекта среди октета соседних пикселов существует хотя бы один, равный 1 и принадлежащий этому объекту. Аналогичные определения связности можно ввести для фона. Заметим, что четырехсвязность фона автоматически означает восьмисвязность объектов и наоборот. Выбор критерия связности оказывает существенное влияние на работу ряда алгоритмов обработки изображений.
Выбор критерия связности оказывает существенное влияние на работу ряда алгоритмов обработки изображений. Это вызвано тем, что в некоторых случаях число объектов на изображении будет зависеть от того, какими считаются объекты: четырехсвязными или восьмисвязными. Внутри связных областей объектов могут встречаться связные области из пикселов фона. Будем называть такие области дырами. Количество дыр также зависит от связности фона.
Программа предоставляет пользователю следующие процедуры морфологической обработки.
Эрозия объекта. Приводит к замене значений граничных пикселов объекта на 0. Пользователь задает форму (квадрат, круг и т.п.) и размер структурирующего элемента, а так же выбирает алгоритм реализации операции (в пространственной, либо частотной области). Эрозия объекта на изображении при единичном размере структурирующего элемента приводит к удалению слоя границы объекта толщиной в 1 пиксел.
Наращение объекта. Приводит к замене значений пикселов фона, граничащих с объектом, на 1. Пользователь задает форму (квадрат, круг и т.п.) и размер структурирующего элемента, а так же выбирает алгоритм реализации операции (в пространственной, либо частотной области). Наращение объекта на изображении при единичном размере структурирующего элемента приводит к добавлению к объекту слоя толщиной в 1 пиксел.
Размыкание. Представляет собой последовательное применение эрозии и наращения со структурирующим элементом, форма и размер которого задается пользователем. Приводит к соединению областей фона, ранее разъединенных узкими участками пикселов объектов.
Замыкание. Представляет собой последовательное применение наращения и эрозии. Приводит к удалению небольших по площади фрагментов фона внутри объектов, например «дыр» (замкнутых областей фона внутри объекта).
Выделение границ бинарных объектов. Соответствует вычитанию из ис-
ходного изображения результата его размыкания, либо вычитанию исходного изображения из результата его замыкания.
Удаление изолированных пикселов объектов. Пикселы, равные 1, все во-
семь соседей которых равны 0, заменяются на 0.
Заполнение изолированных пикселов фона. Пикселы, равные 0, все восемь соседей которых равны 1, заменяются на 1.
21
Уничтожение 8-связности фона. Осуществляется добавлением необходимого количества единиц во фрагменты объектов, связанных только по диагона-
|
0 |
1 |
0 |
0 |
1 |
0 |
|
|
|
|
|
|
|
ли. Например, фрагмент изображения |
1 |
0 |
0 |
заменяется на 1 |
1 |
0 . |
|
1 |
0 |
0 |
1 |
0 |
0 |
|
|
|
|
|
|
|
Соединение пикселов объектов. Пикселы объектов, разъединенных фрагментом фона толщиной в 1 пиксел, соединяются. Например, фрагмент изобра-
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
|
|
0 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
||
жения |
1 |
0 |
1 |
заменяется на |
1 |
1 |
1 . |
|||
|
1 |
0 |
1 |
|
1 |
0 |
0 |
|||
|
|
|
|
|
|
|
|
|
|
|
Удаление центрального пиксела в конфигурациях, похожих на букву “Н”.
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
|
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
В этом случае конфигурации типа |
1 |
1 |
1 |
и |
0 |
1 |
0 |
заменяются соответст- |
||
|
1 |
0 |
1 |
|
1 |
1 |
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
|
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
венно на конфигурации |
1 |
0 |
1 |
и |
0 |
0 |
0 . |
||
|
1 |
0 |
1 |
|
1 |
1 |
1 |
||
|
|
|
|
|
|
|
|
|
|
Удаление внутренних пикселов объектов. Для этого в 0 устанавливаются пикселы объекта, у которых 4 соседних по горизонтали и вертикали пиксела были равны 1, т.е. тоже являлись пикселами объекта. В результате применения этого морфологического фильтра ненулевыми останутся только пикселы границы объекта.
Сжатие объекта. Операция выполняет эрозию объекта с учетом ряда условий для сохранения 8-связнояти замкнутых участков остова. В результате последовательного применения данной операции объекты, не содержащие дыр, превращаются в точку, а объекты с дырами «сжимаются» в 8-связные замкнутые участки остова, проходящие посередине между границами дыр и внешней границей объекта.
Утоньшение объекта. Операция выполняет эрозию объекта с учетом ряда условий для сохранения 8-связности участков остова. В результате последовательного применения данной операции объекты, не содержащие дыр, превращаются в одну или несколько связных линий с минимальным количеством разветвлений остова, а объекты с дырами сжимаются в 8-связные замкнутые участки остова, проходящие посередине между границами дыр и внешней границей объекта.
Утолщение объекта. Операция выполняет наращение объекта с учетом ряда условий для сохранения 4-связности участков фона и является по смыслу обратной операции «утоньшение объекта». Результат данной операции будет значительно отличаться от результатов применения операции «утоньшение объекта» к инвертированному изображению.
22
Удаление ответвлений объекта толщиной в 1 пиксел. В этом случае уда-
ляются пикселы, у которых только один из соседних пикселов установлен в 1, а
|
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
остальные – в 0. Например, фрагмент изображения |
0 |
0 |
1 |
0 |
заменяется на |
|
0 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
1 |
1 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
|
|
|
|
|
0 |
0 |
0 |
0 |
. В результате последовательного применения данной операции к |
0 |
1 |
0 |
0 |
|
|
|
|
|
|
1 |
1 |
0 |
0 |
|
изображению остова объекта на изображении остаются только замкнутые участки остова.
Построение остова (скелета) объекта. Операция выполняет эрозию объ-
екта с учетом ряда условий для сохранения 8-свзности остова. В результате последовательного применения данной операции можно построить остов, представляющий собой связную линию толщиной в 1 пиксел, проходящую посередине объекта.
Деагломерация объектов. Процедуры деагломерации, позволяют разделить соприкасающиеся объекты. Пользователю предлагаются три варианта процедуры: глобальная деагломерация, когда преобразуются сразу все компоненты множества объектов; локальная деагломерация, когда разделяются только указанные пользователем объекты; «ручная» деагломерация, когда в наиболее сложных случаях пользователь сам проводит границу между объектами [96,99]. Пример процедуры деагломерации слипшихся объектов круглой формы с помощью морфологических операций представлен на рис. 4.3. Исходное тестовое изображение полутоновых кругов, показанное на рис. 4.3, а было смоделировано программными средствами разработанного программно-аппаратного комплекса. Пиксели объектов занимают весь диапазон яркостей, и поэтому при бинаризации изображения по какому либо порогу яркости объекты слипаются (рис. 4.3, б).
Для разделения объектов можно использовать следующий подход. Сначала изображение подвергают эрозии до тех пор, пока не исчезнет слипание объектов. При этом объекты не должны в результате эрозии совсем исчезнуть. В рассматриваемом случае необходимо 4 итерации эрозии. Результат эрозии представлен на рис. 4.3, в. Затем объекты на изображении «утолщаются» (строится остов фона). Этот остов (с инверсией контраста) показан на рис. 4.3, г. Результат логического И бинарного изображения и изображения остова фона дает изображение с пикселями фона в местах слипания объектов (рис. 4.3, д). Таким образом, объекты удалось разделить.
23

а) исходное изображение |
б) бинарное изображение |
в) эрозия |
г) остов фона |
д) разделение объектов |
е) спектры эффективных размеров |
Рис. 4.3. Иллюстрация процедуры деагломерации
24

Успешное разделение объектов подтверждает вид спектров эффективных размеров бинарного и полученного после деагломерации изображений. Эти спектры приведены на рис. 4.3, е. Здесь вверху показан спектр исходного бинарного изображения, на котором присутствуют отклики на достаточно широкий диапазон размеров. Внизу же приведен спектр изображения после разделения объектов, на котором присутствуют отклики только для кругов с диаметрами в 30, 40 и 50 пикселей, которые и были смоделированы на исходном полутоновом изображении.
Ниже рассматриваются включенные в состав системы структурноморфологического анализа средства для измерения геометрических характеристик объектов и их взаимного расположения на бинарных электроннооптических изображениях. Пусть в результате порогового ограничения полутонового изображения по некоторому уровню а, получено бинарное изображение, множественное представление которого обозначим как X a . Далее пользователю
предоставляются средства для проведения количественного анализа множества X a . Каждое из локализованных программой связных множеств X ai рассматри-
вается как плоская геометрическая фигура в прямоугольной системе координат XOY. При вычислении морфометрических признаков объектов используются понятия механики твердого тела. В частности, это относится к длинам осей инерции объекта. Направления в теле, совпадающие с полуосями эллипсоида инерции, называют главными осями инерции. Для нахождения главных осей инерции, лежащих в плоскости объекта, используются приводимые ниже соотношения.
Пусть N – количество пикселов на изображении. Все множество пикселов p(x, y), относящихся к объекту, обозначим Ω. Тогда координаты центра масс объекта вычисляются как
xc |
1 |
x , |
yc |
1 |
y . |
(4.1) |
|
|
|||||
|
|
|
|
|
|
|
|
N p( x, y ) |
|
N p( x, y ) |
|
||
Вычислим несколько вспомогательных величин:
U x |
|
|
1 |
|
1 |
(x xc )2 , U y |
|
1 |
|
1 |
( yc |
y)2 . |
(4.2) |
||||
|
|
|
|
|
|
|
|||||||||||
|
12 N p( x, y ) |
|
12 N p( x, y) |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U xy |
1 |
|
(x xc )( yc y) , |
|
|
|
|
|
|
||||||||
|
C |
|
(U x U y )2 |
4U xy2 . |
(4.3) |
||||||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N p( x, y ) |
|
|
|
|
|
|
|
|
|
||||
Тогда длины максимальной Amax и минимальной Amin осей инерции вычисляются как:
|
|
|
|
|
|
|
|
|
Amax 2 |
2 U x U y C , |
Amax 2 |
2 U x U y C . |
(4.4) |
||||
Длины главных осей инерции используются для вычисления эксцентриситета и ориентации объекта. Эксцентриситет определяется с помощью соотношения:
E 2A 1max |
|
|
|
|
(0.5A |
)2 (0.5A )2 . |
(4.5) |
||
|
max |
min |
|
|
Ориентация ai главной оси объекта относительно оси OX определяется как угол в градусах между максимальной осью инерции и осью OX. Ориентация вычисля-
25
ется с помощью формул:
|
U y |
U x |
C |
, U |
|
|
|
, |
|
||
i |
arctg ( |
|
|
|
) |
y |
U |
x |
(4.6) |
||
|
|
|
|||||||||
a |
|
|
2U xy |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
i |
arctg ( |
|
2U xy |
|
) |
, U |
|
U |
|
. |
(4.7) |
|
|
|
y |
x |
|||||||
|
|
|
|||||||||
a |
U x |
U y |
C |
|
|
|
|
||||
|
|
|
|
|
|
|
|||||
Далее вычисляются стандартные геометрические характеристики плоских |
|||||||||||
фигур-объектов периметр Pi и площадь S i . Длина фигуры Li |
вычисляется как |
||||||||||
|
|
a |
|
|
|
a |
|
|
|
a |
|
наибольшее расстояние между точками фигуры в направлении, параллельном главной оси. Ширина H ai – как наибольшее расстояние между точками фигуры в направлении перпендикулярном главной оси. Анизотропность Gai – как отношение длины фигуры к ее ширине. Эффективный размер Dai фигуры – как диаметр
круга, площадь которого совпадает с площадью фигуры. Рассчитываются |
гисто- |
граммы Na P , Na S , Na , Na L , Na H , Na G , Na D зависимости |
числа |
объектов на бинарном изображении от периметра, площади, ориентации, длины, ширины, анизотропности, эффективного размера соответственно. Вычисляются
также «энергетические» характеристики |
изображения – образный спектр |
Fa (n, B) и] спектр эффективных размеров Wa |
D . |
Как установлено в математической морфологии, операции размыкания и |
|
замыкания множеств в евклидовом пространстве с помощью выпуклого множества меняющегося размера (масштаба) позволяют формализовать понятие размера, то есть, возможно, новое определение масштаба, основанное на размыканиях и замыканиях. В литературе исследованы совокупности размыканий и замыка-
ний компактных множеств X R2 , выполняемых с помощью выпуклых компактных структурирующих элементов, например, дисков Dr радиуса r, с тем,
чтобы унифицировать все операции сортировки по размеру (отсеивания) в евклидовых пространствах. Этой параметризованной операции открывания Матерон дал название гранулометрия, а соответствующее им площади назвал распределениями размеров. Убывающая функция A( X Dr ) / A( X ) , где A( ) означа-
ет площадь, r 0 .Образный спектр дискретного бинарного конечного изобра-
жения X |
а |
Z 2 |
относительно структурирующего элемента |
B Z 2 определен в |
|
|
|
|
|
математической морфологии как дифференциальная функция размеров: |
||||
|
|
|
Fa (n, B) A( X a nB) A X a (n 1)B . |
(4.8) |
Для объяснения символического понятия “образный спектр” можно использовать тот факт, что размыкание X а nB представляет собой объединение всех
(nB z) с (nB z) X a , т.е. всех смещенных образов B размера n, которые могут разместиться внутри X a . Следовательно, A( X a nB) является мерой образного содержания X a относительно образа nB, и (4.8) служит мерой изменения
такого образного содержания в зависимости от n. Фактически образный спектр, являющийся неотрицательной функцией для всех B и n, представляет собой гис-
26
тограмму распределения форм по размерам. У него имеется также некоторое концептуальное сходство со спектром Фурье. Образный спектр заключает в себе некоторые виды информации, полезные для описания форм и для многомасштабного анализа изображений. Например, изрезанность границ X a относитель-
но B проявляется в виде вклада в малоразмерную часть образного спектра. Длинные выступы и крупные выдающиеся части X a , которые состоят из образов
sB, проявляются в образном спектре как изолированные импульсы около положительных n s . Наконец, образный спектр может быть определен и для «отрицательных» размеров – если вместо размыканий использовать замыкания; в этом случае импульсы при отрицательных размерах указывают на наличие в X a
значительных заливов или отверстий. |
|
||
Спектр эффективных размеров определяется следующим образом |
|
||
W D = D2 N |
a |
D |
(4.9) |
a |
|
|
|
и представляет собой распределение суммарной площади объектов на бинарном изображении в зависимости от их эффективного размера.
На рис. 4.4, 4.5 представлен полный цикл обработки изображения аморфной ленты состава Fe-Ni-Si-B (размер изображения – 5 5 нм), полученного методом высокоразрешающей электронной микроскопии (ВРЭМ). На рис. 4.4 иллюстрируются процедуры предварительной обработки. Здесь: а – исходное изображение, на котором визуально просматриваются кластеры атомного масштаба (в правом верхнем углу приведен спектр Фурье данного изображения); б – это же изображение, сглаженное нелинейным фильтром, сохраняющим резкими границы объектов; в – изображение атомных кластеров, полученное в результате бинаризации, инверсии и применения ряда морфологических фильтров к предыдущему изображению. Результатом представленной обработки является бинарное изображение атомных кластеров, слабо различимых на исходном полутоновом изображении.
На рис. 4.5 приведены распределения геометрических и «энергетических» характеристик бинарного изображения атомных кластеров (рис. 4.4, в). Здесь: а – распределение эффективных размеров кластеров, б – образный спектр; в – спектр эффективных размеров. Спектр эффективных размеров и образный спектр практически совпадают, но разрешение в спектре эффективных размеров в два раза выше, поскольку действие морфологических операторов, применяемых при расчетах образного спектра, определяется окном, наименьший размер которого [3 3] пиксела.
Далее рассчитываются статистки положения объектов на изображении. Исходными данными для расчета статистик положения являются координаты центров тяжести измеренных объектов. Статистики положения исключительно важны для описания упорядочения в металлических материалах. Конкретно в программе рассчитываются три типа статистик положения.
Морфологический ближний порядок вычисляется в программе как расстояние между объектом и ближайшим к нему соседом. В металловедении понятием ближний порядок характеризуют свойство атомов группироваться около
27

ближайших соседей на определенном расстоянии. Программа рассчитывает статистики морфологического ближнего порядка (среднее, дисперсию и т.д.), а также распределение этого параметра. По характеру этого распределения можно принять решение о наличии либо отсутствии ближнего порядка в расположении структурных элементов изображения и оценить его численное значение.
а) |
б) |
в)
Рис. 4.4. Полутоновая и морфологическая обработка ВРЭМ-изображения
Статистики «ближние направления» характеризуют ориентационное упорядочение элементов микроструктуры в ближних координационных сферах. Ближняя координационная сфера в программе определяется как примыкающее к выделенному элементу кольцо, для элементов которого 0,8rcp r 1,2rcp , где rcp
– среднее значение морфологического ближнего порядка, r – расстояние от элементов кольца до его геометрического центра. Для каждого объекта изображения программа фиксирует направления на соседей, центры которых находятся в пределах кольца.
28
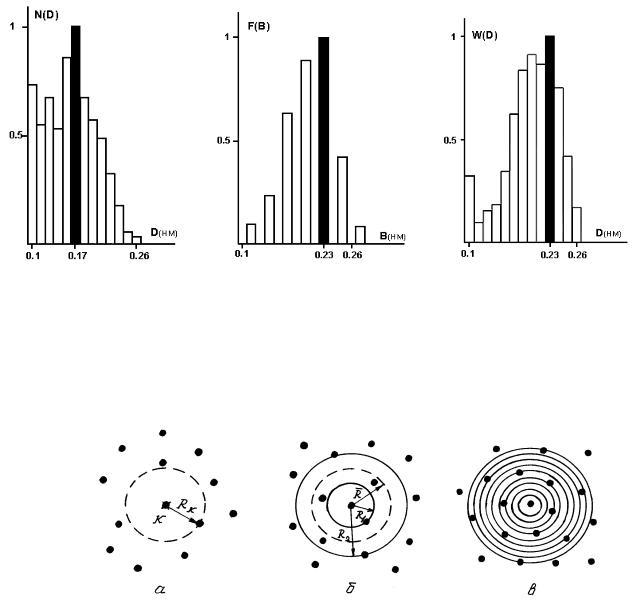
а) |
б) |
в) |
|
Рис. 4.5. Гистограммы бинарного ВРЭМ изображения
По результатам анализа всех объектов изображения рассчитывается результирующее распределение Ca ближних направлений (РБН). Наличие в распреде-
лении выделенных направлений свидетельствует о присутствии на изображении областей с регулярной структурой.
Рис. 4.6. Пояснения к алгоритмам расчета статистик положения:
а) – «ближний порядок» – расстояние от пробного объекта до ближайшего соседа (усредняется впоследствии по всем пробным объектам); б) – выбор «ближней координационной сферы» при расчете статистик «ближних направлений» и «координационных чисел»; в) – геометрия кольцевых областей при расчете «МФРР»
Морфологическая функция радиального распределения (МФРР) рассчитывается как усредненное по всем объектам изображения распределение Фa r чис-
ла соседей для каждого объекта в зависимости от расстояния r до этого объекта. Рис. 4.6 поясняет схему расчета статистик положения. Используемая в программе схема расчета МФРР полностью совпадает с известным определением функции радиального распределения для атомов, которая обычно рассчитывается по результатам дифракционных экспериментов.
На рис. 4.7, а, б приведены МФРР и РБН бинарного изображения атомных кластеров. МФРР в данном случае подобна функции радиального распределения атомов в аморфных металлических материалах. РБН имеет два выделен-
29
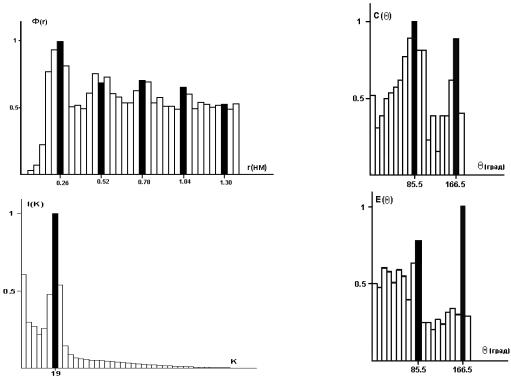
ных направления, соответствующих преимущественной ориентации решеток кластеров атомного размера. Эти результаты совпадают с результатами спектрального анализа исходного полутонового изображения, представленными на рис. 4.7, в, г. На рис. 4.7, в показано распределение I k ( k - номер гармоники в спектре) спектральной энергии изображения в системе кольцевых зон, которая обычно используется для определения особенностей частотного состава спектра. На рис. 4.7, г приведено распределение E спектральной энергии в системе угловых секторов ( - угловое положение сектора), которая часто используется для описания свойств изотропности/анизотропности анализируемого изображения. Выделенная 19-я гармоника в распределении I k совпадает с основным периодом функции Ф r . Совпадают также и выделенные направления распределений E и C . Таким образом, функции Ф r и C дают важную информацию о взаимном расположении объектов на изображении.
а) |
б) |
в) |
г) |
|
Рис. 4.7. Гистограммы взаимного положения кластеров на бинарном изображении и спектральных характеристик ВРЭМизображения
Отметим, что по виду функции I k сложно без специальной обработки получить информацию о геометрических характеристиках атомных кластеров. Существующие в настоящее время методики количественного анализа спектров позволяют оценивать функцию распределения объектов на изображении только в предположении одинаковой формы и изотропности в их пространственном распределении.
30
