5. Решение слау размерности

Рассмотрим однородную СЛАУ:

(3.1)

Данная система всегда имеет хотя бы одно решение, например тривиальное .

Теорема: Однородная СЛАУ имеет нетривиальное решение тогда и только тогда, когда ранг основной матрицы системы меньше числаеё неизвестных.

Следствие: Квадратная однородная СЛАУ имеет нетривиальное решение тогда и только тогда, когда определитель основной матрицы этой системы равен нулю.

Если ранг матрицы однородной системы равен , то система имеетлинейно независимых решений:, называемыхфундаментальной системой решений.

Решения являются линейно независимыми, если ранг матрицы составленной из координатных строк этих векторов равенчислу этих решений.

Теорема: (о структуре решений однородных СЛАУ). Пусть произвольная фундаментальная система решений однородной системы линейных уравнений. Тогда любое решение системы представляет собой линейную комбинацию решений:

(3.2)

Здесь общее решение однородной системы,- произвольные постоянные, афундаментальная система решений, (частные решения однородной системы), найденная при условии, что свободные неизвестныепо очереди приравниваются 1, а остальные при этом равны 0. Неизвестные называются базисныминеизвестными.

Решение неоднородной системы (1.1) в общем случае определяется следующей теоремой:

Теорема: (о структуре решения неоднородной СЛАУ): Общее решение неоднородной СЛАУ определяется формулой:

(3.3)

где - общее решение соответствующей однородной системы, а- частное решение неоднородной системы.

Для более простого нахождения частного решения, удобно взять свободные неизвестные равными нулю.

6. Варианты заданий

Найти общее решение неоднородной системы уравнений методом Гаусса:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

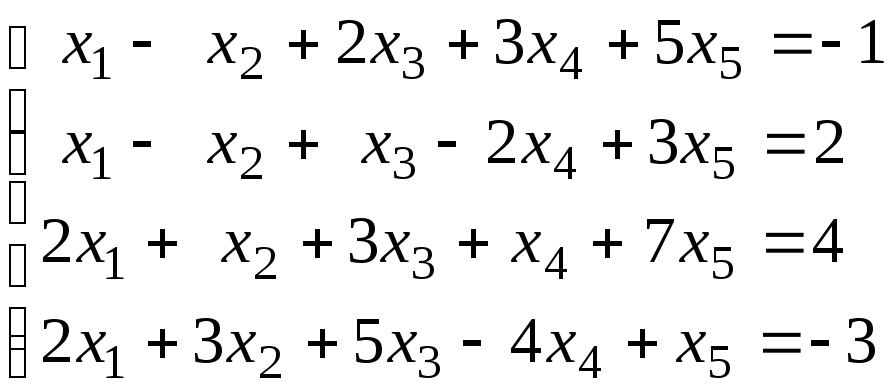7. ;

8. ;

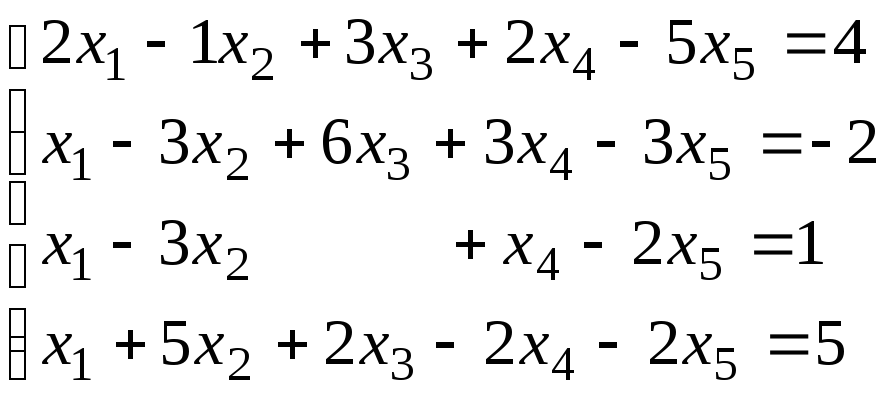9. ;

10. .

7. Решение типового варианта

1. Найти общее решение неоднородной системы уравнений

.

Решение: Для нахождения решения системы выпишем расширенную матрицу:

.

Приведем ее к нижнему треугольному виду элементарными преобразованиями со строками. Для этого:

1. умножаем первую строку на и складываем со второй;

2. умножаем первую строку на и складываем с третьей строкой;

3. умножаем первую строку на и складываем с четвертой строкой.

1) , 2);

3) .

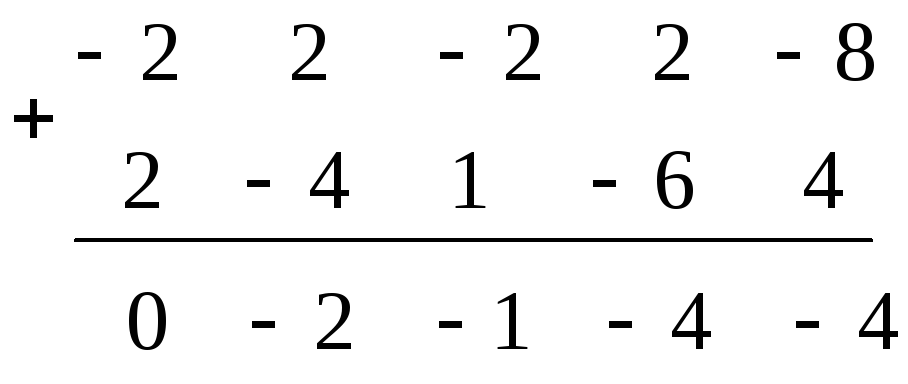Полученные результаты записываем в матрицу эквивалентную исходной:

~

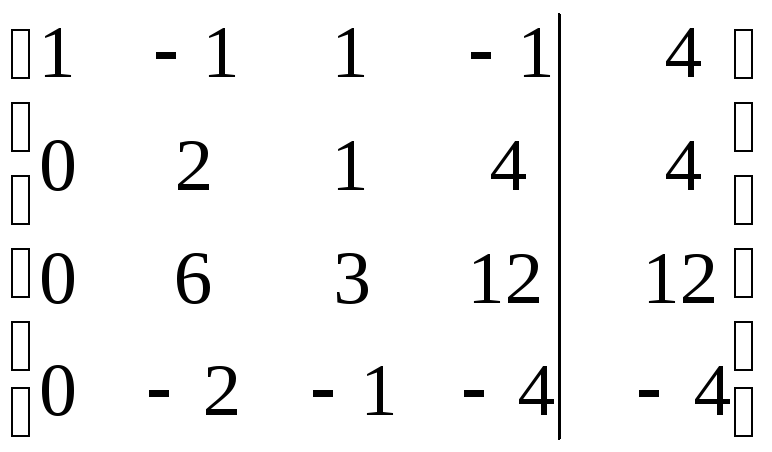
В данной приведенной матрице если все элементы третьей строки поделить на три, а элементы четвертой строки умножить на минус один, то они совпадут с элементами второй строки. Это означает, что три последние строки являются линейно зависимыми (выражаются одна через другую) и, следовательно, две из них можно обнулить.

.

Количество ненулевых строк (хотя бы один элемент не равен нулю) в основной (до вертикальной черты), и в расширенной матрицах, равно двум, следовательно, , поэтому согласно теореме Кронеккера-Капелли система совместна т.е. имеет решение.

По приведенной матрице запишем неоднородную систему эквивалентную исходной системе:

.

Определим количество базисных и свободных переменных. Общее число переменных системы равно четырем а. Следовательно, число базисных переменных равно двум (), а число свободных переменных определим соотношением.

Согласно теореме о фундаментальном решении неоднородной системы: .

Найдем общее решение однородной системы, которое зависит от значения двух свободных неизвестных: .

По исходной приведенной системе запишем однородную: .

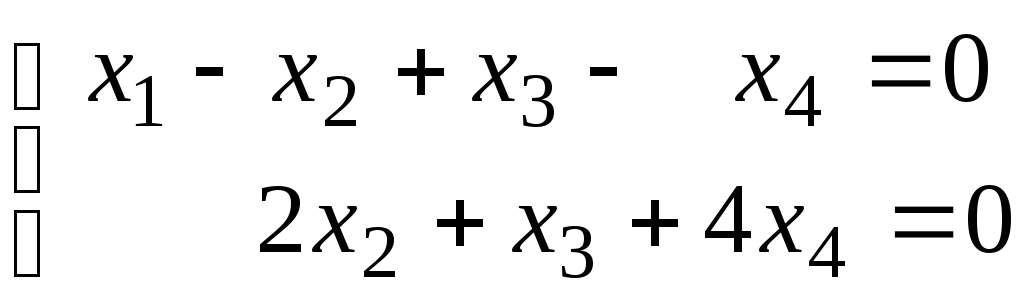В качестве базисных неизвестных выберем , т.к. минор, полученный на пересечении первых двух столбцов и строк,отличен от нуля. Свободными являются оставшиеся неизвестные.

Перенесем свободные неизвестные вправо:

.

Для определения частных решений выберем свободные неизвестные произвольными константами.

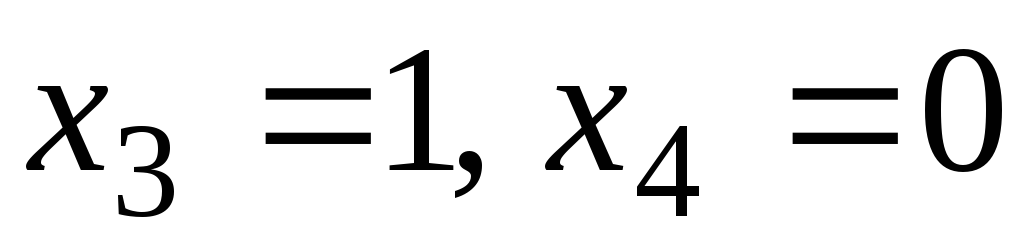1. Для определения , например, возьмем. Получим систему

, .

Откуда ,.

Получили первое частное решение системы: .

2. Для определения возьмем. Получим систему

. Откуда ,.

Получили второе частное решение системы: .

Запишем общее решение однородной системы:

.

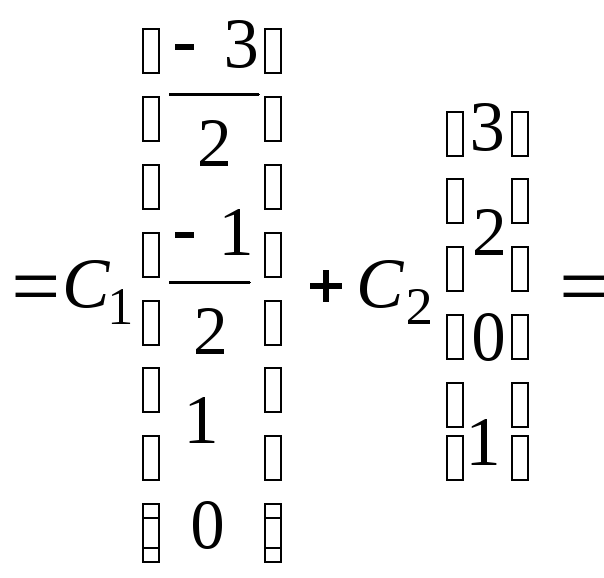
Найдем - некоторое частное решение неоднородной системы.

Для этого выберем свободные переменные в виде и подставим в систему. Получим:

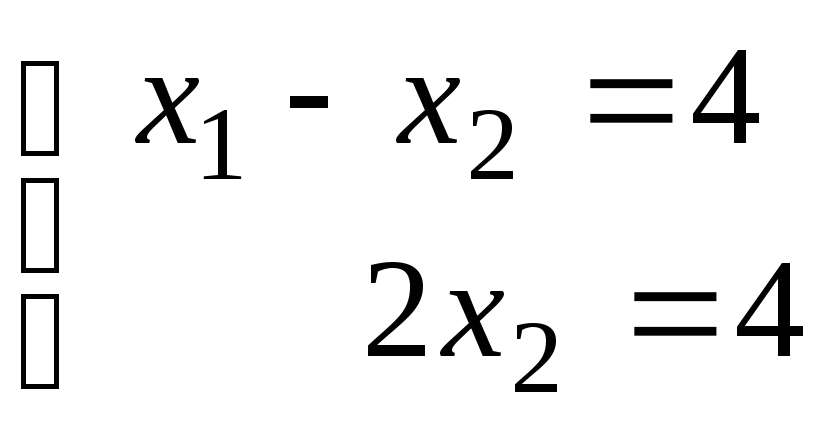. Откуда ,.

Частное решение имеет вид:

Убедимся в правильности вычислений, сделаем проверку

.

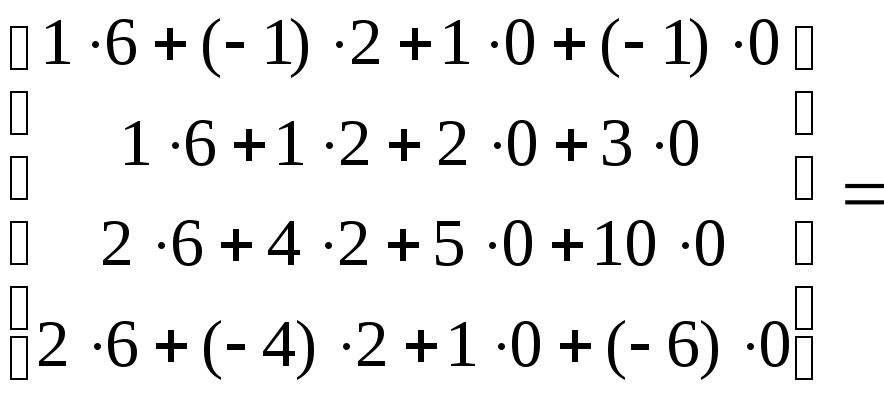
Вычислено верно. Окончательно имеем:

.