3. Варианты заданий

Проверить систему на совместность и в случае совмесности решить ее:

1) по формулам Крамера;

2) Методом Гаусса;

3) Матричным методом.

1. , 2.;

3. , 4.;

5. , 6.;

7. , 8.;

9. , 10..

4. Решение типового варианта

1. Проверить систему на совместность и в случае совмесности решить ее:

1) по формулам Крамера;

2) Методом Гаусса;

3) Матричным методом.

Решение: Нам задана СЛАУ размерности. В случае квадратной системы ее совместность можно проверить, не прибегая к вычислению рангов основной и расширенной матрицы. Достаточно вычислить определитель основной матрицы системы. Если последний отличен от нуля, то система совместна и имеет единственное решение.

Выпишем определитель основной матрицы системы и вычислим его:

1) Для нахождения решения системы по формулам Крамера, вычислим дополнительные определители по формулам (2.3). Для этого в основном определителе системы-ый столбец заменяем столбцом свободных членов.

, ,.

Теперь, пользуясь формулами Крамера (2.2), найдем:

; ;.

Убеждаемся в правильности решения. Подставим найденные значения в исходную систему:

Получили три тождества, значит решение найдено верно. Ответ: .

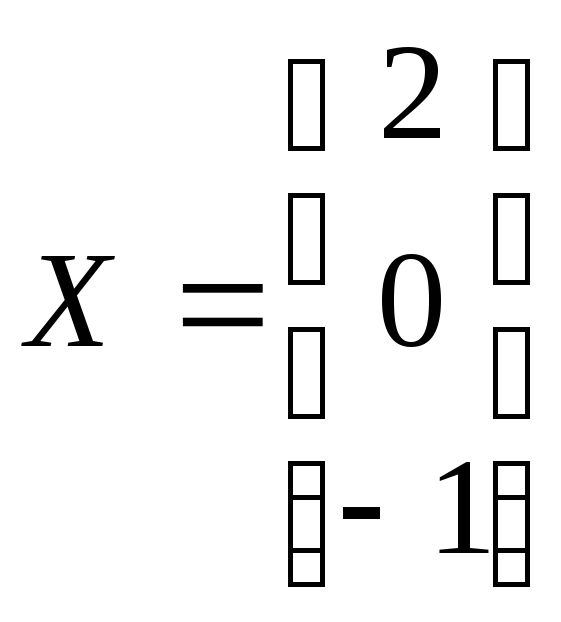2) Для решения системы методом Гаусса выпишем расширенную матрицу системы и приведем ее к треугольному виду (прямой ход метода Гаусса), используя элементарные преобразования строк.

Расширенная матрица системы имеет вид:

Для наглядности, мы отделили столбец свободных членов от основной матрицы вертикальной чертой. Приведем матрицу к нижнему треугольному виду. Для удобства поменяем местами первую и вторую строки, это не изменит решения системы:

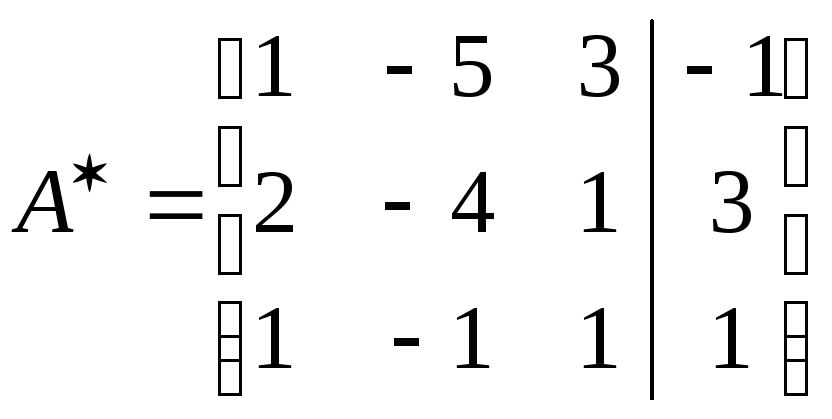
Обнулим элементы первого столбца. Для этого:

1. первую строку умножим на и сложим ее со второй строкой;

2. первую строку умножим на и сложим ее с третьей строкой.

1) , 2).

Запишем результаты вычислений в матрицу, при этом первую строку оставляем без изменения:

~

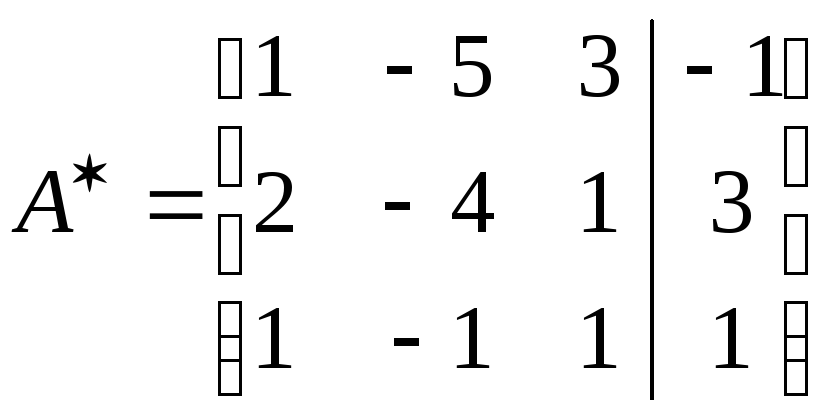Обнулим элементы второго столбца. Для этого:

1) третью строку умножим на и прибавим к ней вторую строку.

Получили приведенную матрицу, эквивалентную исходной расширенной:

.

Найдем решение системы обратным ходом. Для этого по полученной приведенной матрице запишем систему эквивалентную начальной:

Из последнего уравнения получаем: .

Подставляем найденное значение во второе уравнение и определяем :

, ,

И, наконец, из первого уравнения находим переменную :

, ,.

Ответ полностью совпал с первым решение по методу Камера.

3) Матричный метод.

Для решения системы определим обратную матрицу по формуле , где- присоединенная матрица системы, состоящая из алгебраических дополнений основной транспонированной матрицы:

.

Напомним, алгебраическим дополнением называется выражение вида , гдеминор, получаемый из основного определителя удалением из него-ой строки и-го столбца. Найдем

, ;,;

, ;

, ;

.

Обратная матрица имеет вид: . Убедимся в правильности ее вычисления, используя формулу::

Матрица вычислена верно.

Используя формулу (2.4) найдем неизвестные:

.

Матричным методом система решена верно.

Ответы к вариантам:

1) , 2), 3), 4);

5) , 6), 7), 8);

9) , 10).