
Metodichki / Комплексные числа и действия над ними
.pdf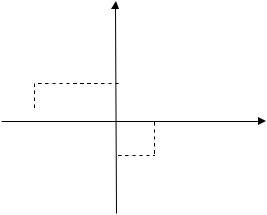
|
4x5 7x3 5x2 3x 4 |
|
|
9x3 5x2 6x 2 |
||||
8) |
|
|
, |
|
|
|
; |
|
|
x2 2x 1 |
|
|
x 2 |
||||
|
6x5 3x4 2x3 7x 6 |
|
8x3 7x2 x 4 |
|||||
9) |
|
|
, |
|
|
; |
|
|
x2 3x 7 |
|
|||||||
|
|
|
x 2 |
|||||
|
7x5 9x4 3x2 4x 1 |
|
|
2x3 6x2 7x 1 |
||||
10) |
|
|
, |
|
|
. |
||
|
x2 5x 7 |
|
|
x 3 |
||||
Решение типового задания
I.Нарисовать комплексные числа на комплексной плоскости, если
z1 3 4i, |
z2 7 2i. |
Решение: |
|
Для каждого комплексного числа выпишем действительную х и
мнимую у части согласно формуле (1.1):
x1 Rez1 3, y1 Im z1 4, x2 Re z2 7, y2 Im z2 2.
На комплексной плоскости отметим две точки с соответствующими координатами:z1(3; 4), z2( 7;2) (рис.3).
|
|
|
у |
|
|
z2 |
|
|
2 |
|
|
|
|
|
3 |
х |
|
|
|
|
|||
7 |
|
|
|||
|
4 |
|
|
|
z1 |
|
|
|
|
||
Рис.3
II. Возвести комплексное число в квадрат, если: z 5 7i.
Решение:
Воспользуемся формулой сокращенного умножения
(a b)2 a2 2ab b2, тогда z2 (5 7i)2 25 70i 49i2
13

применяя формулу (1.2) к последнему слагаемому, окончательно получаем
z2 24 70i
III. Найти аргумент комплексного числа, если: z1 2 2i, z2 7
 3 7i.
3 7i.
Решение:
Для нахождения аргумента комплексного числа воспользуемся формулой (1.6). Определим действительные x и мнимые y части заданных
комплексных чисел: x1 2, y1 |
2, x2 7 |
3, |
y2 7. |
|||||||||||||||||
Для числа z1 : x1 0, |
y1 0, следовательно |
|
|
|
|
|
|
|
||||||||||||
1 arg z1 arctg |
y1 |
arctg |
|
2 |
arctg( 1) |
|
. |
|
|
|
||||||||||
x1 |
|
|
|
|||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
4 |
|
|
|
|
|
||||
Для числа z2 : x2 0, |
|
y2 0, следовательно |
|
|
|
|
|
|
|
|||||||||||
2 arg z2 arctg |
7 |
|
|
arctg |
|
1 |
|
|
|
|
|
5 |
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
7 |
3 |
3 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
6 6 |
|
||||||||||
IV. Выполнить действия: |
|
z1 z2, z1 z2, z1 |
z2, z1 : z2, если известно, |
|||||||||||||||||
что: z1 3 4i, z2 5 6i.
Решение:
Рассматривая комплексные числа как двучлены выполним действия сложения, вычитания и умножения:
z1 z2 (3 4i) ( 5 6i) 3 5 4i 6i 2 2i; z1 z2 (3 4i) ( 5 6i) 3 5 4i 6i 8 10i;
z1 z2 (3 4i) ( 5 6i)
3 ( 5) 3 (6i) ( 4i) ( 5) ( 4i) (6i)
15 18i 20i 24i2
15 38i 24 ( 1) 15 24 38i 9 38i;
14

Найдем |
отношение |
z1 |
|
|
|
3 4i |
|
. Домножим |
числитель и знаменатель |
||||||||||||||
z2 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
5 6i |
|
|
|
|
||||||
дроби на число, сопряжённое к знаменателю |
|
|
z |
2 5 6i. Согласно |
|||||||||||||||||||
формуле (1.10) получим: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
z |
|
(3 4i) ( 5 6i) |
|
|
|
|
15 18i 20i 24i2 |
|||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 5)2 62 |
|
|
|||||||
|
z2 |
|
( 5 6i) ( 5 6i) |
|
|
|
|
|
|||||||||||||||
|
39 2i |
|
39 |
i |
2 |
. |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
61 |
61 |
|
61 |
|
|
|
|
|
|
|
|
||||||||
V. Перевести комплексное число ( 7
 3 7i)4 в показательную форму и возвести в степень. Ответ записать в алгебраической форме.
3 7i)4 в показательную форму и возвести в степень. Ответ записать в алгебраической форме.
Решение:
Для того, перевести комплексное число в показательную форму,
необходимо найти его модуль и аргумент . Для этого воспользуемся
формулами (1.5) и (1.6). определим действительную и комплексную части
числа: x 7
 3 0, y 7 0. Получаем:
3 0, y 7 0. Получаем:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 y2 ( 7 3)2 72 14; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
arctg |
y |
arctg |
7 |
|
|
arctg |
1 |
|
|
|
|
5 |
. |
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
x |
7 |
3 |
|
3 |
6 6 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
i |
||||
Тогда в показательной форме число имеет вид: z 2 |
|
|
|
|
|||||||||||||||||
|
49 e 6 . |
||||||||||||||||||||
Возведём данное число в четвёртую степень используя формулу (3.6):
z4 |
|
5 |
i 4 |
|
5 |
i 4 |
|
10 |
i |
|
|
|
|||||||
14 e 6 |
|
(14)4 e 6 |
38416 e 3 |
||||||
|
|
|
|
|
|
|
|
|
|
Учитывая, что функция ei имеет период T 2 , окончательно получаем:
|
4 6 |
|
4 |
|
|
4 |
|
|
|
i |
|
|
2 i |
|
i |
||
|
|
|||||||
|
|
|
|
|||||
z4 38416 e 3 |
38416 e |
3 |
|
38416 e 3 . |
||||
15
Для того, чтобы перевести число в алгебраическую форму z x iy
определим x и y по формулам (1.3):
x cos , x 38416 cos 4 38416 ( 1) 19208;
|
3 |
|
2 |
|
|
|
|
|
||
|
|
4 |
|
|
|
|
|
) 19208 |
|
; |
y sin , |
y 38416 sin |
38416 ( |
|
|
3 |
|||||
|
|
|
3 |
|||||||
|
2 |
|
||||||||
|
3 |
|
|
|
|
|
||||
z 19208 i19208 |
3. |
|
|
|
|
|
||
VI. Найти |
модуль |
комплексного |
числа |
z 7 3i, |
z |
2 |
4e 3i , |
|
|
|
|
|
|
1 |
|
|
|
z3 0,85(cos4 isin4) и записать комплексно сопряжённое число. |
||||||||
Решение: |
|
|
|
|
|
|
|
|
Число |
z1 |
задано |
в алгебраической форме, |
для нахождения модуля |
||||
воспользуемся |
формулой (1.5): |
x 7, |
y 3, |
следовательно |
||||
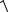
 72 ( 3)2
72 ( 3)2 
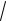 58.
58.
Число z2 задано в показательной форме z ei (1.8), откуда следует,
что 4.
Число z3 задано в тригонометрической форме z (cos isin ) (1.5)
следовательно 0,85.
Определим комплексно сопряжённые числа по формулам (1.9). Получаем:
z1 7 3i, z2 4e3i , z3 0,85(cos4 isin4).
VII. Для данного комплексного числа (3 
 2i) 2( 4 5i)3 найти модуль.
2i) 2( 4 5i)3 найти модуль.
Решение:
Выражение (3 
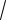 2i) 2( 4 5i)3 представляет из себя произведение
2i) 2( 4 5i)3 представляет из себя произведение
двух комплексных чисел z1 3 |
2i и z2 4 5i возведенных в |
степень. Для каждого из них вычислим модуль:
1 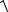
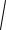 32 (
32 (
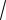 2)2
2)2 
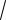 11, 2
11, 2 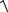
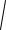 ( 4)2 52
( 4)2 52 
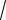 41.
41.
16

Согласно формуле Муавра (3.6), при возведении комплексного числа в степень, его модуль также возводится в данную степень, т.е.
2 |
|
|
|
2 |
|
1 |
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
( 11) |
|
|
|
|
, |
2 |
( 41) |
|
41 41; |
||||||
|
|
|
||||||||||||||
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
||
При перемножении двух комплексных чисел. их модули перемножаются
|
|
|
|
|
|
|
|
z 2 z |
3 |
|
2 |
3 |
|
1 |
41 |
|
|
41 41 |
. |
||||||
|
|
||||||||||||||||||||||||
(3.1), (3.2). Следовательно |
|
|
41 |
||||||||||||||||||||||
|
2 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
2 |
11 |
|
|
11 |
|
||||
|
|
|
3 |
|
, если |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
VIII. Вычислить |
z |
z 2 2 |
|
|
i |
задано, изобразить |
найденные |
||||||||||||||||||
|
3 |
||||||||||||||||||||||||
решения на комплексной плоскости. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для вычисления 3 |
|
переведём комплексное число в |
|
|
|
|
|||||||||||||||||||
z |
|
|
|
|
|||||||||||||||||||||
тригонометрическую форму, определив модуль и аргумент. |
|
|
|
|
|||||||||||||||||||||
z 2 2 |
|
i, |
x 2 0, |
y 2 |
|
0; |
|
|
|
|
|
|
|
||||||||||||
3 |
3 |
|
|
|
|
|
|
|
|||||||||||||||||
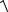
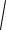 ( 2)2 (2
( 2)2 (2
 3)2
3)2 
 16 4;
16 4;
arctg 2
 3 arctg
3 arctg
 3 2 .
3 2 .
|
|
2 |
|
|
|
3 3 |
В тригонометрической форме получим: |
||||||
|
|
|
2 |
|
2 |
|
|
|
|||||
z 2 2 |
3i 4 cos |
|
isin |
|
|
|
3 |
|
|||||
|
|
|
3 |
|
||
Для извлечения корня порядка n 3, воспользуемся формулой (3.7): |
|
|
|||||||||||||||||||
где k 0,1, 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
2 |
2 0 |
2 |
2 0 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
3 |
|
|
|
3 |
|
|
3 |
|
3 |
|
|
|
||||||||
z0 |
4 cos |
|
|
isin |
|
|
isin |
|
|||||||||||||
|
|
|
4 |
cos |
|
|
|
|
|||||||||||||
|
|
3 |
|
3 |
9 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4(0,77 i0,64) 1,22 i 1,02; |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
17
|
|
|
|
|
|
|
|
2 |
|
2 1 |
2 |
2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
8 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|
|
|
|||||||||||||||||||||||
|
3 |
4 cos |
|
|
|
|
|
|
|
|
|
|
|
|
3 4 |
|
|
||||||||||||||||||||||
z |
|
|
|
isin |
|
|
|
|
|
|
cos |
|
|
isin |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
9 |
|
|
9 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
4( 0,94 i0,34) 1,49 i 0,54; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
2 2 |
2 |
|
2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
14 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
z2 |
|
3 |
4 |
cos |
|
|
|
|
isin |
|
|
|
|
|
|
|
3 |
|
|
4(cos |
isin |
) |
|||||||||||||||||
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
9 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3
 4(0,17 i0,98) 0,27 i 1,56.
4(0,17 i0,98) 0,27 i 1,56.
Построим графическое представление корней:
1)Вычерчиваем окружность радиуса R n
 1,6
1,6
2)Откладываем угол 2 и на его пересечении с окружностью
n 9
отмечаем корень z0.
3) Вписываем в окружность правильный треугольник (рис. 4).
у
2 z0 9
z1
1,6 х
z2
Рис. 4
IX. Решить квадратное уравнение x2 5x 9 0.
Решение: Решим данное квадратное уравнение через дискриминант:
D b2 4ac ( 5)2 4 9 25 36 9;
x1,2 b 
 D 5
D 5 
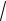 9 .
9 .
2a 2
18

Используя формулу (1.2), получим: 
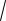 9
9 
 1 9
1 9 
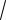 1
1 
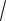 9 i 3. Тогда
9 i 3. Тогда
х |
|
5 3i |
|
5 |
|
3 |
i. Или x |
|
5 |
|
3 |
i, x |
|
|
5 |
|
3 |
i. Что подтверждает |
|
|
|
|
|
|
|
|
|||||||||||
1,2 |
2 |
2 |
2 |
1 |
2 |
2 |
|
2 |
2 |
2 |
|
|||||||
теорему о том, что если многочлен имеет комплексный корень, то он имеет и
комплексно сопряженный корень.
Х. Найти частное и остаток от деления.
3x3 2x2 4x 1 |
2x5 3x3 7x2 2x 4 |
|||
|
, |
|
|
. |
|
x2 |
|
||
x 5 |
6x 7 |
|||
Решение: Для определения частного и остатка воспользуемся формой деления в столбик:
3x3 |
|
2x2 |
4x |
1 |
x 5 |
||
3x3 |
|
15x2 |
|
|
|
|
|
|
|
|
3x2 13x 61 |
||||
|
|
|
|
|
|
|
|
|
|
13x2 |
4x |
|
|
|
|
|
|
13x2 |
65x |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
|
|
|
|
|
|
61x |
|
||
|
|
|
|
61x |
305 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
306 |
|
|
При делении получим: 3x2 13x 61 - частное, 306 - остаток.
3x3 2x2 4x 1 3x2 13x 61 306 .
|
x 5 |
|
x 5 |
|
2x5 |
3x3 |
7x2 |
2x 4 можно представить как: |
|
2x5 |
0x4 |
3x3 |
7x2 |
2x 4. Делим в столбик: Найти частное и |
остаток от деления.
2x5 0x4 |
3x3 |
7x |
||
2x5 12x4 14x3 |
|
|||
|
|
|
|
|
|
|
12x4 |
17x3 |
7x |
|
|
|
|
|
2 2x |
4 |
|
x2 6x 7 |
2x3 12x2 89x 611
2
19

|
|
12x4 72x3 |
84x2 |
|
|
|
|
|
||||
|
|
|
|
89x3 |
77x2 |
2x |
|
|
|
|
||
|
|
|
|
89x3 |
534x2 |
623x |
|
|
|
|
||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
611x2 |
625x |
4 |
||||
|
|
|
|
|
|
611x2 |
3666x |
4277 |
||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4291x |
4281 |
|||
При делении получили: 2x3 12x2 89x 611 - частное |
||||||||||||
4291x 4281 - остаток |
|
|
|
|
|
|||||||
|
2x5 3x3 7x2 2x 4 |
2x3 12x2 |
89x 611 |
4291x 4281 |
. |
|||||||
|
|
|
||||||||||
|
|
x2 6x 7 |
|
|
|
|
|
x2 6x 7 |
||||
Дополнительные задания.
1. Найти действительные решения уравнения:
(3x i)(2 i) (x iy)(1 2i) 5 6i.
2. Найти модуль и аргумент комплексного числа:
11 i i 3 20, ( 1 i
3 20, ( 1 i
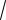 3)60.
3)60.
3.Изобразить на комплексной плоскости множество точек:
1z 2 i 2, Re z 2,Im z 1.
4.Записать в комплексной форме уравнение прямой:
2x 3y 1 0.
5. Вычислить: 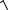
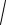 2 i2
2 i2
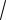 3.
3.
20
Список используемой литературы
1.Любимова О.Н., Дегтярева Н.Е. Линейная алгебра и аналитическая геометрия. Владивосток.: изд-во ДВГТУ, 2008г. - 167с.
2.:Клетеник Д.В., Сборник задач по аналитической геометрии. С-Петербург.:
Профессия, 2006. – 200с.
3.Кадомцев С.Б. Аналитическая геометрия и линейная алгебра. М.: Физматлит, 2001. -160с.
|
Оглавление |
|
1 |
Комплексные числа и формы их записи |
3 |
2 |
Действия над комплексными числами, заданными в |
5 |
|
алгебраической форме |
|
3 |
Действия над комплексными числами, заданными в |
6 |
|
тригонометрической или в показательной форме |
|
4 |
Практикум |
7 |
5 |
Решение типового задания |
11 |
6 |
Дополнительные задания. |
18 |
7 |
Список используемой литературы |
18 |
21
КОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НАМИ
Методические указания Составители: Дегтярева Н.Е. Корректор:
Технический редактор Подписано в печать . Формат Печать офсетная. Усл.печ.л. Уч.-изд.л. Тираж 100 экз. Заказ
__________________________________________________________________
Издательство ДВГТУ.690650, Владивосток, Пушкинская, 10 Типография издательства ДВГТУ, 690650, Владивосток, Пушкинская, 10
22
