
4.3. Трехфазные цепи при соединении приемников звездой
Соединение звездой при симметричной нагрузке. При соединении приемников звездой концы фаз приемника соединены в общий узел N'. При этом концы всех фаз генератора соединены в общий узел N, а начала фаз — с нагрузкой — звездой сопротивлений.
Если узлы N и N' соединить проводом, называемым нейтральным, с сопротивлением ZN, то получим четырехпроводную цепь (рис. 4.7, а). Сопротивления проводов, связывающих источник с нагрузкой, можно учесть в сопротивлениях нагрузки Za ,Zb ,Zc.
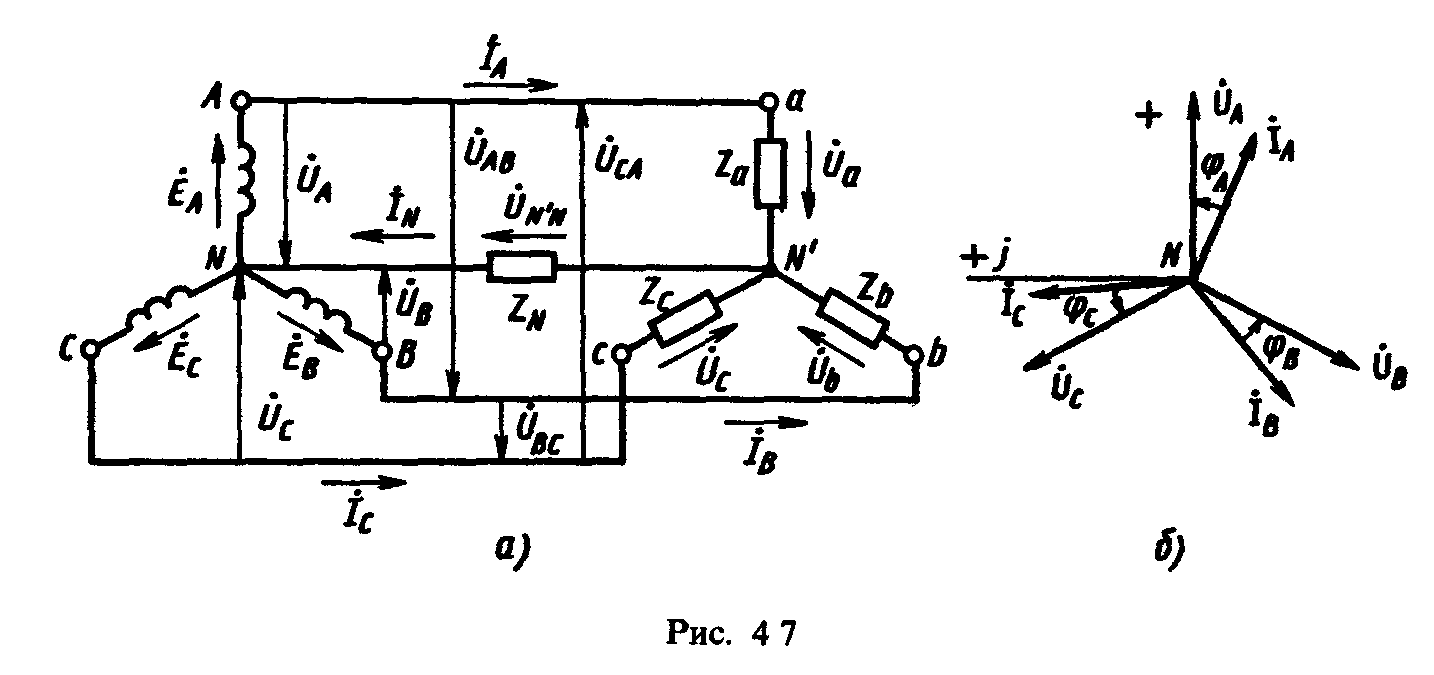
Так как при соединении звездой фазы генератора соединены последовательно с фазами нагрузки, линейные токи одновременно являются и фазными токами как в фазах генератора, так и в фазах нагрузки:
![]() (4.8)
(4.8)
За условные положительные направления линейных токов IА, IВ, IС принимают направления от источника к нагрузке, а за положительное направление тока в нейтральном проводе - от нагрузки к источнику.
Согласно первому закону Кирхгофа, ток в нейтральном проводе
![]() (4.9)
(4.9)
При симметричной
нагрузке
![]() поэтому токи в фазах приемника равны
по значению и сдвинуты по фазе на один
и тот же угол относительно соответствующих
напряжений, т. е. φA
= φB
= φC
= φ. Векторная диаграмма напряжений и
токов для симметричной нагрузки
представлена на рис. 4.7, б. Из диаграммы
видно, что ток в нейтральном проводе
равен нулю (IN
= 0), так как
поэтому токи в фазах приемника равны
по значению и сдвинуты по фазе на один
и тот же угол относительно соответствующих
напряжений, т. е. φA
= φB
= φC
= φ. Векторная диаграмма напряжений и
токов для симметричной нагрузки
представлена на рис. 4.7, б. Из диаграммы
видно, что ток в нейтральном проводе
равен нулю (IN
= 0), так как
![]() .
Таким образом, если нагрузка равномерная,
то необходимость в нейтральном
проводе отпадает. Трехфазная цепь без
нейтрального провода является
трехпроводной.
.
Таким образом, если нагрузка равномерная,
то необходимость в нейтральном
проводе отпадает. Трехфазная цепь без
нейтрального провода является
трехпроводной.
Рассмотрим четырехпроводную цепь (рис. 4.7, а) более подробно. Найдем для этой цепи напряжение между нейтральными точками N и N', или смещение нейтрали, по методу двух узлов:
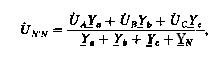 (4.10)
(4.10)
где
![]() - комплексы проводимостей фаз приемника;YN
= 1/ZN
-комплекс проводимости нейтрального
провода. Так как при симметричной
нагрузке Ya = Yb = Yc, то (4.10) можно переписать
в виде
- комплексы проводимостей фаз приемника;YN
= 1/ZN
-комплекс проводимости нейтрального
провода. Так как при симметричной
нагрузке Ya = Yb = Yc, то (4.10) можно переписать
в виде
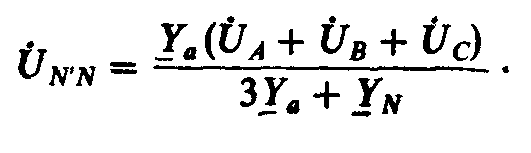 (4.11)
(4.11)
При симметричной
системе напряжений имеем
![]()
![]() а значит, согласно
(4.11), UNN
=0. Так как ток в нейтральном проводе
а значит, согласно
(4.11), UNN
=0. Так как ток в нейтральном проводе
![]() то при симметричной нагрузкеIN
= 0. Следовательно, еще раз можно
подчеркнуть, что при симметричной
нагрузке напряжение между нейтральными
точками N и N' и ток в нейтральном проводе
равны нулю.
то при симметричной нагрузкеIN
= 0. Следовательно, еще раз можно
подчеркнуть, что при симметричной
нагрузке напряжение между нейтральными
точками N и N' и ток в нейтральном проводе
равны нулю.
Согласно второму закону Кирхгофа, для контуров (см. рис. 4.7, а) NAaN'N, NBbN'N, NCcN'N находим
![]() (4.12) Так как при
симметричной нагрузке UN’N
=0, то из (4.12) следует, что
(4.12) Так как при
симметричной нагрузке UN’N
=0, то из (4.12) следует, что
![]()
Итак, зная фазные напряжения и сопротивления нагрузки, находим токи в каждой фазе приемника:
![]() (4-13)
(4-13)
Так как при симметричной нагрузке токи в фазах приемника равны, то достаточно определить ток только в одной из фаз трехфазной цепи.
Соединение
звездой при несимметричной нагрузке.
При несимметричной нагрузке
сопротивления приемника не одинаковы,
т. е. Za ≠
Zb
≠ Zc.
Для несимметричных нагрузок применяют
четырехпроводные цепи, так как между
точками N и N'
появляется напряжение UN’N
и напряжения на фазах нагрузки различны.
При этом нарушается соотношение между
фазными и линейными напряжениями ![]() причем
на одних фазах нагрузки напряжение
становится большим, а на других —
меньшим, чем
причем
на одних фазах нагрузки напряжение
становится большим, а на других —
меньшим, чем ![]()
Наличие нейтрального
провода в цепи с несимметричной нагрузкой
позволяет выравнивать напряжение на
фазах приемника и поддерживать их
неизменными, равными фазным напряжениям
источника Uл
/![]() ,
т. е. нейтральный провод обеспечивает
симметрию фазных напряжений приемника.
Иначе говоря, при наличии нейтрального
провода, когда ZN
= 0, даже при несимметричной нагрузке
фазные напряжения приемника равны
друг другу и соблюдается соотношение
между фазными и линейными напряжениями
,
т. е. нейтральный провод обеспечивает
симметрию фазных напряжений приемника.
Иначе говоря, при наличии нейтрального
провода, когда ZN
= 0, даже при несимметричной нагрузке
фазные напряжения приемника равны
друг другу и соблюдается соотношение
между фазными и линейными напряжениями
![]() .
.
Если нагрузка несимметрична (Za ≠ Zb ≠ Zc) и нейтральный провод имеет конечное сопротивление ZN, то напряжение UN’N между нейтральными точками N' и N определяется по формуле (4.10), а напряжения на фазах нагрузки — по формулам (4.12). Тогда токи в схеме рис. 4.7, а

Если напряжения источника UA, UB, UC образуют симметричную систему, то при отсутствии нейтрального провода и при UN'N ≠ 0 напряжения на фазе нагрузки Ua, Ub и Uc несимметричны, что видно из векторной топографической диаграммы, приведенной на рис. 4.8. Особенностью этой диаграммы является то, что каждой точке электрической цепи А, В, С, N и N' соответствует определенная точка на диаграмме.
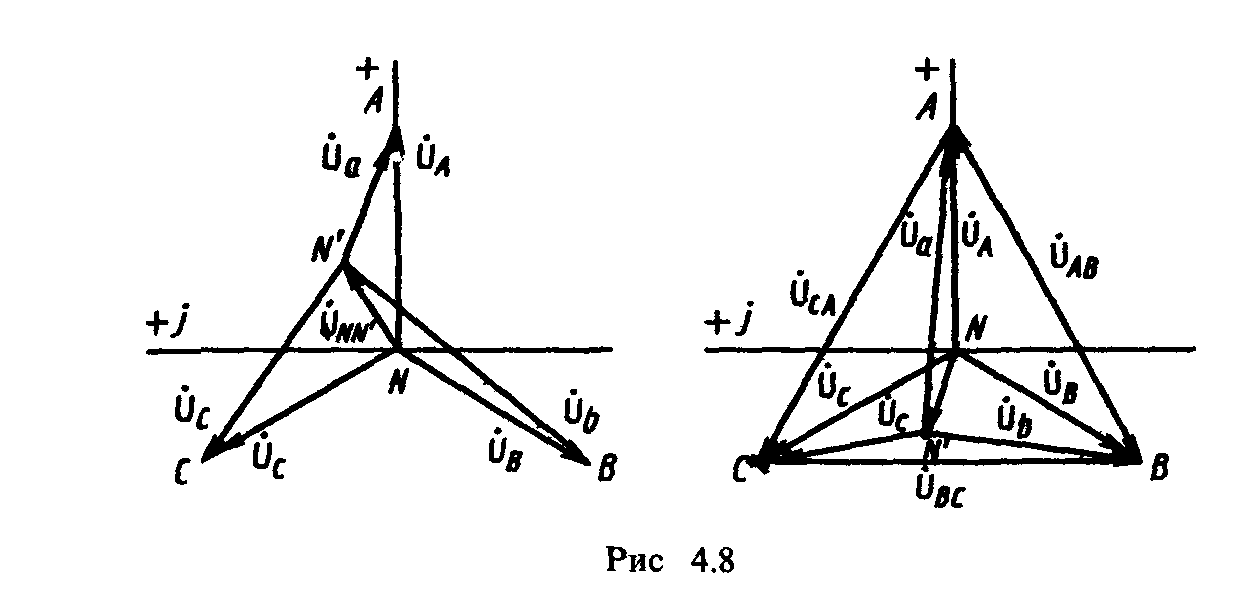
При этом расположение этих точек на диаграмме должно быть таким, чтобы отрезок, соединяющий любые точки на диаграмме, по длине и фазе определял напряжение между соответствующими точками цепи.
Напряжения на фазах нагрузки тем больше отличаются друг от друга, чем больше напряжение UN'N. Из выражения (4.10) и из топографической диаграммы (рис. 4.8) следует, что напряжение между нейтральными точками UN'N будет изменяться при изменении нагрузки в любой фазе, при этом с изменением UN'N будет изменяться напряжение всех фаз приемника.
Чтобы напряжения на фазах нагрузки были одинаковыми, необходимо иметь UN'N = 0, что может быть получено двумя способами. Во-первых, выравниванием нагрузки в фазах приемника, когда YA = YB = YC = = Yф, а значит, согласно (4.10),

так как![]()
В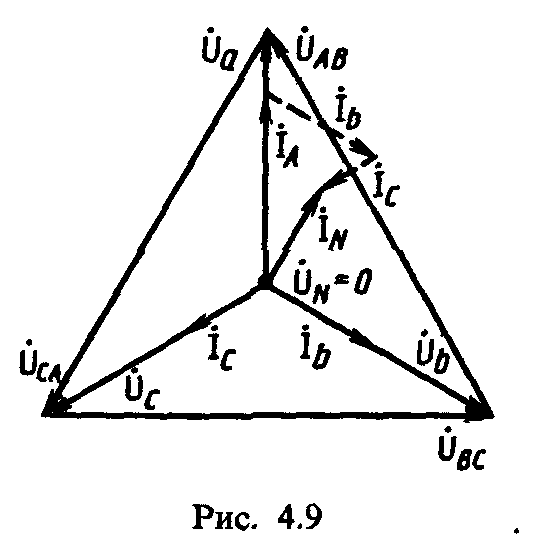 о-вторых,
если имеется нейтральный провод с
сопротивлением ZN’N
= 0 (или YN’N
= ∞ ), то напряжение UN'N,
согласно (4.10), также принимает нулевое
значение независимо от нагрузки фаз.
Для этого случая построена векторная
диаграмма (рис. 4.9). При обрыве нейтрального
провода (ZN
= ∞) и несимметричной нагрузке
напряжение UN'N
станет максимальным.
о-вторых,
если имеется нейтральный провод с
сопротивлением ZN’N
= 0 (или YN’N
= ∞ ), то напряжение UN'N,
согласно (4.10), также принимает нулевое
значение независимо от нагрузки фаз.
Для этого случая построена векторная
диаграмма (рис. 4.9). При обрыве нейтрального
провода (ZN
= ∞) и несимметричной нагрузке
напряжение UN'N
станет максимальным.
В фазах нагрузки
могут возникнуть перенапряжения, поэтому
в нейтральный провод плавкий предохранитель
не ставят. Приемники электрической
энергии можно подразделить на
трехфазные и однофазные. К числу
трехфазных относятся трехфазные
электрические двигатели, имеющие
симметричные обмотки и обеспечивающие
равномерную нагрузку фаз. Такие
электродвигатели включают в трехфазную
цепь звездой без нейтрального провода
Однофазные приемники, к которым относятся
электрические лампы, нагревательные
приборы и ряд других приемников, всегда
подключают к четырехпроводной цепи.
Эти приемники подключаются на фазное
напряжение, которое в
![]() раз меньше линейного напряжения сети.
раз меньше линейного напряжения сети.
Пример 4.1. К трехфазной линии напряжением Uл=380 В подключен несимметричный трехфазный приемник, соединенный звездой с нейтральным проводом (рис. а)). Активные и реактивные сопротивления фаз приемника соответственно равны: Ra = 19 Ом, Xa = 0 Ом, Rb= 8 Ом, Хb = 6 Ом, Rс = 24 Ом, Хc = 18 Ом. Сопротивлениями проводов можно пренебречь. Определить ток в фазах приемника, в линейных проводах и в нейтральном проводе.

а)
Рисунок к примеру 4.1.
Решение. Токи в линейных проводах и фазах приемника одинаковы и рассчитываются по закону Ома:
![]() -
-
Фазное напряжение
![]()
Комплексные фазные напряжения:

Комплексные сопротивления фаз:

Токи в фазах приемника и проводах линии:
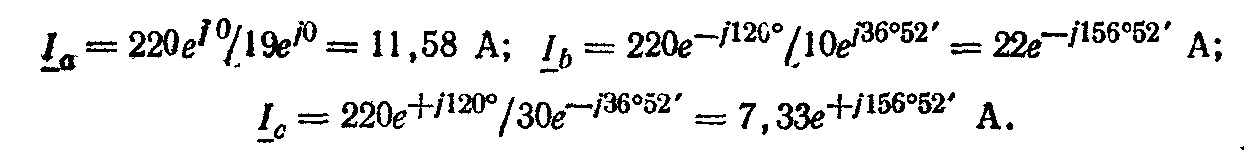
Ток в нейтральном проводе
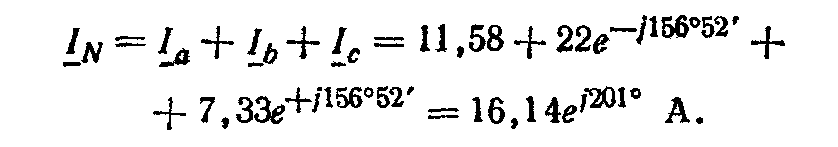
Для построения топографической диаграммы напряжений выберем масштаб напряжений. В выбранном масштабе строим топографическую диаграмму напряжений. При построении векторной диаграммы токов учтем, что токи в фазах сдвинуты относительно фазных напряжений на разные углы сдвига фаз: φа = 0 — нагрузка чисто активная (Х=0), φb = 36°52' — нагрузка активно-индуктивная, φc = - 36052'— нагрузка активно-емкостная.
 Действующее
значение тока в нейтральном проводе
равно 16,14 А, а его начальная фаза ψN
= 2010.
На диаграмме (рис. б)
строим векторы токов
Действующее
значение тока в нейтральном проводе
равно 16,14 А, а его начальная фаза ψN
= 2010.
На диаграмме (рис. б)
строим векторы токов
б)
Рисунок к примеру 4.1.
с учетом углов сдвига фаз. Вектор тока в нейтральном проводе можно построить двумя способами: или как сумму векторов или непосредственно отложить вектор IN в соответствии с расчетными данными.
 Пример
4.2. К
трехпроводной трехфазной сети с линейным
напряжением Uл=220 В подключен приемник,
фазы которого соединены звездой,
(рис.а)).
Заданы сопротивления Rа
= 10 Ом, Rb
= 5 Ом, Хb
= 9,66 Ом, Хс
= 10 Ом. Определить токи в ветвях, построить
совмещенную топографическую диаграмму
напряжений и векторную диаграмму токов.
Пример
4.2. К
трехпроводной трехфазной сети с линейным
напряжением Uл=220 В подключен приемник,
фазы которого соединены звездой,
(рис.а)).
Заданы сопротивления Rа
= 10 Ом, Rb
= 5 Ом, Хb
= 9,66 Ом, Хс
= 10 Ом. Определить токи в ветвях, построить
совмещенную топографическую диаграмму
напряжений и векторную диаграмму токов.
а)
Рисунок к примеру 4.2.
Решение. Фазные напряжения источника образуют симметричную систему

Комплексные сопротивления фаз приемника:
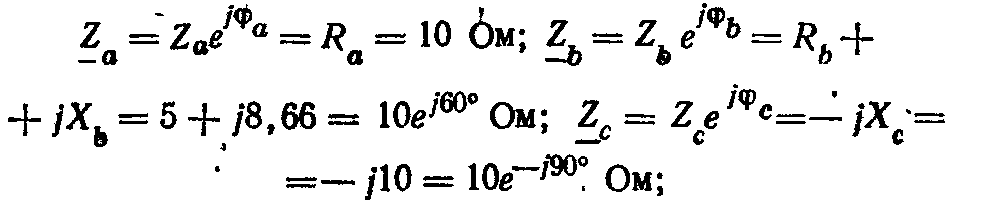
их комплексные подводимости

Смещение нейтрали


Рисунок к примеру 4.2.
Фазные напряжения приемника:

Фазные токи и токи в линии:

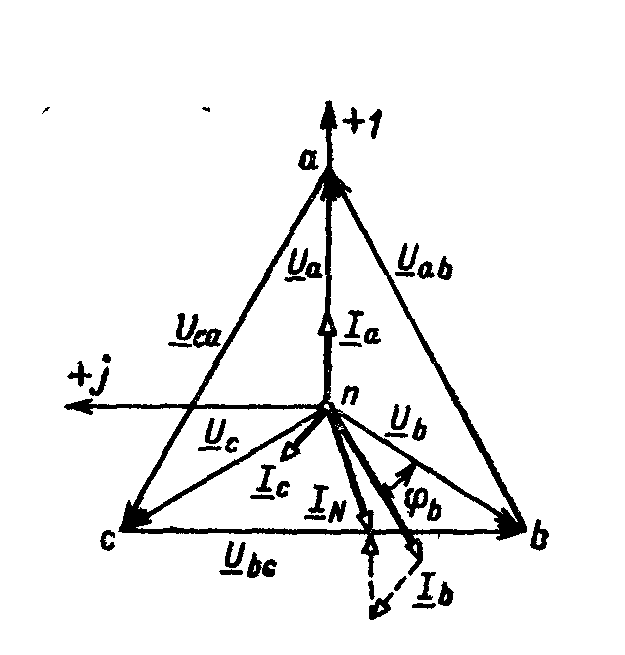
Для построения векторных диаграмм выбираем масштабы напряжения и тока. Строим симметричную топографическую диаграмму напряжений генератора ( рис. б)) и вектор смещения нейтрали UnN = 84e j205° В. Векторы, соединяющие точку n и точки а, b, с, соответственно будут векторами фазных напряжений приемника Ua, Ub, Uc. Из точки n строим векторы токов Ia, Ib, Iс учетом сдвига фаз относительно напряжений φa= 0°, φb= 60°, φc= — 90°.
Топографическая диаграмма напряжений показывает, что из-за смещения нейтрали симметрия фазных напряжений приемника нарушается: Ua = 206 В вместо Uф = 127 В; Uc = 145,6 В; Ub=75,5 В.
